Diferencia entre notaciones de O grande y tilde

En el análisis asintótico de algoritmos, a menudo encontramos términos como Big-Oh, Omega, Theta y Tilde, que describen el rendimiento de un algoritmo. 
Puede consultar los siguientes enlaces para obtener más información sobre el análisis asintótico:

1. Análisis de Algoritmos 
2. Notaciones diferentes
3. Diferencia entre Big Oh, Big Omega y Big Theta

En este artículo vamos a ver la diferencia entre las dos notaciones: Big Oh y Tilde.

1. Notación Big Oh (O) :
esta notación se usa básicamente para describir el límite superior asintótico . Matemáticamente, podemos describirlo como:

f(n) = O(g(n)) 
if there exist positive constants c and 
n0 such that 
0 <= f(n) <= c*g(n) 
for all n >= n0

La notación anterior muestra que en el punto n=n0, el crecimiento de la función g(n) aumenta gradualmente. En los algoritmos siempre tratamos con valores más grandes de n, es decir, n→∞. Entonces, también podemos definir la notación Big-Oh como:

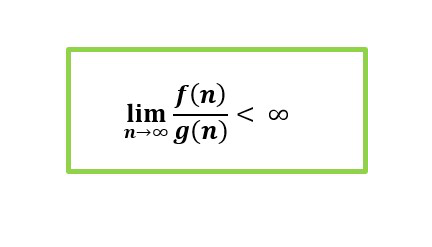
Por lo tanto, f(n) = O(g(n)) si el valor límite anterior se encuentra en el rango [ 0 , ∞ )

Ejemplo – 

2. Notación Tilde (~):
La notación Tilde se usa cuando queremos hacer una aproximación simple de una función compleja. Simplemente elimina los términos de orden inferior. Se denota por ~g(n).
Si f(n)~g(n) indica que el valor de f(n)/g(n) tiende a 1 para un valor mayor de n. Matemáticamente, podemos expresarlo como:

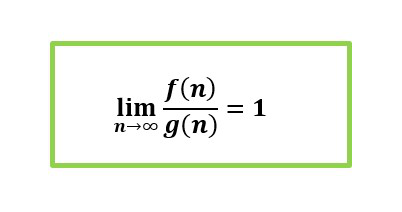
El ejemplo 
1.   se puede escribir como ~ porque cuando dividimos ambas funciones y encontramos el límite para un valor mayor de n, se convertirá en 1.

2 – En un árbol AVL antes de insertar o eliminar una clave, primero comparamos y encontramos la ubicación de la clave. El número de comparaciones requeridas en el peor de los casos es:

h+1, where h is the height of the tree. 
The height will be , since AVL tree is a height balanced tree. 

Por lo tanto, podemos reemplazar el valor de h en la expresión y se convierte en:

Podemos ignorar el término de orden inferior y se convierte en ~ . Entonces, el número de comparaciones en un árbol AVL se aproxima a ~ .

Algunos puntos importantes sobre la notación ~ en el análisis asintótico:

• Sigue la propiedad de la relación de equivalencia .
• Es idéntica a la notación theta grande . Hay una pequeña diferencia en la constante arbitraria, ya que en la notación theta grande puede haber diferentes valores para las constantes en el límite inferior y en el límite superior, pero en el caso de Tilde, siempre obtenemos el valor f/g como 1 o tiende hacia 1.

Las diferencias entre las notaciones Big Oh y Tilde son:

S No-	Gran Oh (O)	tilde (~)
1	Generalmente define el límite superior de un algoritmo.	Dado que es similar a la notación theta, define tanto el límite superior como el límite inferior de un algoritmo.
2	La constante arbitraria en el caso de la notación Big Oh es c, que es mayor que cero. 0 <= f(n) <= c*g(n) ; c>0, n>=n0	Aquí, la constante siempre será 1 ya que al dividir f por g o g por f siempre obtenemos 1. Por lo tanto, da una aproximación más nítida de un algoritmo.
3.	Si la complejidad temporal de cualquier algoritmo es  ,está dada por O( ) y se ignora la constante.	Aquí, por la misma complejidad de tiempo será ~( ). Esta constante 1/3 no tiene sentido ya que en el análisis asintótico solo nos interesa saber sobre el crecimiento de una función para un valor mayor de n.
4.	Se utiliza principalmente en el análisis asintótico, ya que siempre estamos interesados ​​en conocer el límite superior de cualquier algoritmo.	Big theta se usa principalmente en lugar de la notación Tilde, ya que en el caso de Big Theta podemos tener diferentes constantes arbitrarias, c1 para el límite superior y c2 para el límite inferior.
5.	Define el peor de los casos.	En su mayoría define el caso promedio.

Para más detalles, consulte:
Diseño y Análisis de Algoritmos .