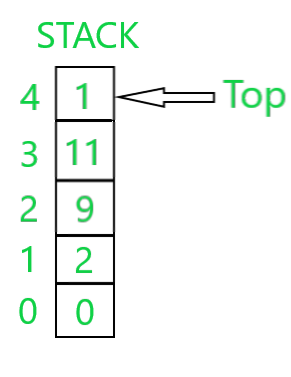
Pila: una pila es una estructura de datos lineal en la que los elementos se pueden insertar y eliminar solo desde un lado de la lista, llamado la parte superior . La inserción se denomina operación push y la eliminación se denomina operación pop en el caso de la pila. El orden de inserción y eliminación puede ser LIFO (Last In First Out), es decir, el último elemento insertado en la pila también se insertará primero. arriba lo mismo
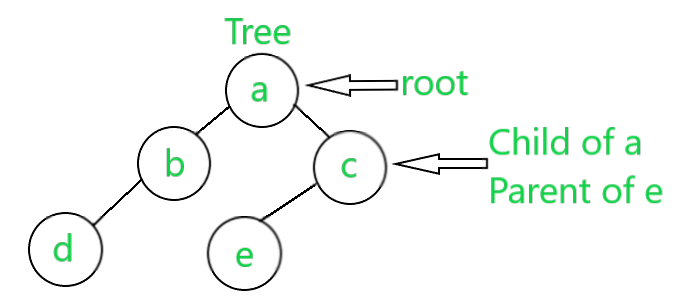
Árbol: Un árbol es un conjunto finito de uno o más Nodes tal que:
- Hay un Node especialmente designado llamado raíz .
- Los Nodes restantes se dividen en N>=0 conjuntos disjuntos T 1 , T 2 , T 3 , …, T N , donde T 1 , T 2 , T 3 , …, T N se denomina el subárbol de la raíz.
Cada Node tiene un padre específico y puede o no tener un Node hijo. Cada Node contiene un valor y referencias a los hijos. Es una especie de estructura de datos de gráfico pero no tiene ciclos y está completamente conectado . a
A continuación se muestra la diferencia tabular entre la pila y el árbol:
| No. S. |
Parámetro |
Pila |
Árbol |
| 1 | Naturaleza básica | Estructura de datos lineal | Estructura de datos no lineal |
| 2 | Noción básica | parte superior de la pila | La raíz del árbol |
| 3 | Sucesor | Elemento empujado antes del elemento de referencia | La noción de hijo y padre existe |
| 4 | Orden de Inserción | Elementos insertados en la parte SUPERIOR de la pila | Depende del tipo de árbol. |
| 5 | Orden de eliminación | Elementos eliminados de la parte SUPERIOR de la pila | Depende del tipo de árbol. |
| 6 | Complejidad de inserción | O(1) | Depende del tipo, por ejemplo AVL- O (log 2 N). |
| 7 | Complejidad de eliminación | O(1) | Depende del tipo, por ejemplo AVL- O (log 2 N). |
| 8 | buscando | O(1) | Depende del tipo, por ejemplo AVL- O (log 2 N). |
| 9 | Encontrar mínimo | EN) | Depende del tipo, por ejemplo Min Heap- O (log 2 N). |
| 10 | encontrar máximo | EN) | Depende del tipo, por ejemplo Min Heap- O (log 2 N). |
| 11 | Esta vacio | O(1) | Mayormente O(1) |
| 12 | Implementación | Uso de arrays y listas enlazadas | Se puede implementar utilizando una array y un tipo de Nodes definido por el usuario |
| 13 | Tipos | No existen tipos | Muchos tipos como Binary Tree, AVL Tree, nary Tree, etc. |
| 14 | Aplicaciones | Evaluación de expresiones, Backtracking , gestión de memoria, etc. | Búsqueda rápida, insertar, eliminar, etc. |
Publicación traducida automáticamente
Artículo escrito por parthbanathia y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA