En lógica digital, las entradas y salidas de una función tienen la forma de números binarios (valores booleanos), es decir, los valores son cero (0) o uno (1). Por lo tanto, la lógica digital también se conoce como ‘lógica booleana’. Estas entradas y salidas pueden denominarse ‘Variables booleanas’. La variable booleana de salida de una señal digital se puede expresar en términos de variables booleanas de entrada que forman la ‘expresión booleana’.
La representación de la expresión booleana se puede realizar principalmente de dos formas. Son los siguientes:
- Formulario de suma de productos (SOP)
- Formulario de producto de sumas (POS)
Nota:
si el número de variables de entrada es n, entonces el número total de combinaciones en el álgebra booleana es 2 n .
Si el valor de la variable de entrada (let A) es:
- Cero (0) – a es BAJO -Debe representarse como A’ (Complemento de A)
- Uno (1) – a es ALTO – Debe representarse como A
En lógica booleana,
AND is represented as '.' A AND B is written as 'A.B' OR is represented as '+' A OR B is written as 'A+B'
Por ejemplo, considerando el número de variables de entrada =3, digamos A, B y C.
El número total de combinaciones es: 2 3 =8.
| A | B | C |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 0 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
| 1 | 1 | 1 |
Suma de Productos (SOP):
Es una de las formas de escribir una expresión booleana. Como sugiere el nombre, se forma sumando (operación OR) los términos del producto. Estos términos de productos también se denominan «términos mínimos». Los términos mínimos se representan con ‘m’, son el producto (operación Y) de variables booleanas en forma normal o complementada.
Por lo tanto, SOP es la suma de minitérminos y se representa como:
F en SOP = 
m (0, 3)
Aquí, F es la suma de minterm0 y minterm3.
Por ejemplo:
A=0, B=0, C=0 Minterm is A'.B'.C' A=1, B=0, C=1 Minterm is A.B'.C
Considere una función X, cuya tabla de verdad es la siguiente:
| A | B | C | X |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 0 |
La función X se puede escribir en forma SOP sumando todos los términos mínimos cuando X es ALTO (1).
Al escribir SOP, se debe seguir la siguiente convención:
If variable A is Low(0) - A'
A is High(1) - A
X (SOP) = m (1, 3, 6)
= A’.B’.C+ A’.BC+ ABC’
Producto de sumas (POS):
como su nombre indica, se forma multiplicando (operación AND) los términos de la suma. Estos términos de suma también se denominan «términos máximos». Los términos máximos se representan con ‘M’, son la suma (operación OR) de variables booleanas en forma normal o complementada.
Por lo tanto, POS es producto de maxterms y se representa como:
F en POS = 
M (1, 2) Aquí, F es producto de maxterm1 y maxterm2.
Por ejemplo:
A=0, B=1, C=0 Maxterm is A+B'+C A=1, B=1, C=1 Maxterm is A'+B'+C'
Considere una función X, cuya tabla de verdad es la siguiente:
| A | B | C | X |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 0 |
La función X se puede escribir en forma POS multiplicando todos los términos máximos cuando X es BAJO (0).
Al escribir POS, se debe seguir la siguiente convención:
If variable A is Low(0) - A
A is High(1) - A'
X (POS) =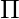 
M(0, 2, 4, 5, 7)
= (A+B+C).(A+B'+C).(A'+B+C).(A'+B+C').(A'+B'+C')
Diferencia entre SOP y POS:
| S. No. | COMPENSACIÓN | TPV |
|---|---|---|
| 1. | Una forma de representar expresiones booleanas como suma de términos de productos. | Una forma de representar expresiones booleanas como producto de términos de suma. |
| 2. | SOP utiliza minitérminos. Minterm es producto de variables booleanas en forma normal o complementada. | POS utiliza maxterms. Maxterm es la suma de variables booleanas en forma normal o complementada. |
| 3. | Es suma de minitérminos. Los minitérminos se representan como ‘m’ | Es producto de maxterms. Maxterms se representan como ‘M’ |
| 4. | SOP se forma considerando todos los minitérminos, cuya salida es ALTA (1) | POS se forma considerando todos los maxterms, cuya salida es LOW(0) |
| 5. | Al escribir minitérminos para SOP, la entrada con valor 1 se considera como la variable en sí misma y la entrada con valor 0 se considera como complemento de la entrada. | Al escribir maxterms para POS, la entrada con valor 1 se considera como el complemento y la entrada con valor 0 se considera como la variable en sí. |