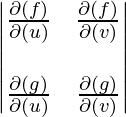Diferenciales o Derivadas en MATLAB

La diferenciación de una función y = f(x) nos dice cómo cambia el valor de y con respecto al cambio en x. También se puede denominar como la pendiente de una función.

La derivada de una función f(x) con respecto a x se representa como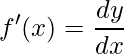 

MATLAB permite a los usuarios calcular la derivada de una función utilizando el método diff(). Las diferentes sintaxis del método diff() son:

• f’ = diferencia(f)
• f’ = diferencia(f, a)
• f’ = diferencia(f, b, 2)

f’ = diferencia(f)

Devuelve la derivada de la función f(x) con respecto a la variable x.

Ejemplo 1:

% Create a symbolic expression in variable x
syms x
f = cos(x);
disp("f(x) :");
disp(f);
 
% Derivative of f(x)
d = diff(f);
disp("Derivative of f(x) :");
disp(d);

Producción :

Ejemplo 2: Evaluar la derivada de una función en un valor específico usando subs(y,x,k).

• subs(y,x,k) , da el valor de la función y en x = k .

% Create a symbolic expression in
# variable x
syms x
f = cos(x);
disp("f(x) :");
disp(f);
 
% Derivative of f(x)
d = diff(f);
val = subs(d,x,pi/2);
 
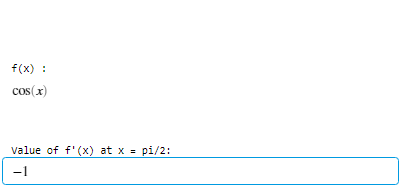
disp("Value of f'(x) at x = pi/2:");
disp(val);

Producción :

f’ = diferencia(f, a)

• Devuelve la derivada de la función f con respecto a la variable a .

% Create a symbolic expression in variable x
syms x t;
f = sin(x*t);
disp("f(x) :");
disp(f);
 
% Derivative of f(x,t) wrt t
d = diff(f,t);
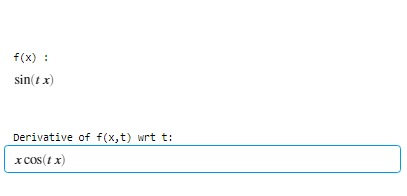
disp("Derivative of f(x,t) wrt t:");
disp(d);

Producción :

f’ = diferencia(f, b, 2)

Devuelve la doble derivada de la función f con respecto a la variable b .

Ejemplo 1:

% Create a symbolic expression in
% variable x,n
syms x n;
f = x^n;
disp("f(x,n) :");
disp(f);
 
% Double Derivative of f(x,n) wrt x
d = diff(f,x,2);
disp("Double Derivative of f(x,n) wrt x:");
disp(d);

Producción :

De la misma manera, también puede calcular la derivada de orden k de la función f usando diff(f,x,k) .

Ejemplo 2: 

Cálculo de la derivada parcial 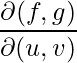 } usando array jacobiana y determinante.

% Create a symbolic expression in variable
% u and v
syms u v;
f = u^2;
g = sin(v)*(3*u);
disp("f(u,v) :");
disp(f);
disp("g(u,v) :");
disp(g);
 
% Jacobian matrix of function f(u,v) and
% g(u,v)
J = jacobian([f; g], [u v]);
disp("Jacobian matrix :");
disp(J);
 
% Determinant of Jacobian matrix
d = det(J);
disp("Determinant of Jacobian matrix:");
disp(d);

Producción :