Diferentes operaciones en arrays

Posted on by Rudeus Greyrat

Para una introducción a las arrays, puede consultar el siguiente artículo: Introducción a la array 
En este artículo, discutiremos varias operaciones con arrays y sus propiedades: 

Suma de arrays: 
la suma de dos arrays A m*n y B m*n da como resultado una array C m*n . Los elementos de C son la suma de los elementos correspondientes en A y B que se pueden mostrar como: 

1

El algoritmo para la suma de arrays se puede escribir como: 

for i in 1 to m
   for j in 1 to n
      cij = aij + bij

C++

// C++ Program for matrix addition
 
#include <iostream>
using namespace std;
 
int main()
{
 
    int n = 2, m = 2;
    int a[n][m] = { { 2, 5 }, { 1, 7 } };
    int b[n][m] = { { 3, 7 }, { 2, 9 } };
 
    int c[n][m];
    for (int i = 0; i < n; i++)
        for (int j = 0; j < n; j++) {
            c[i][j] = a[i][j] + b[i][j];
        }
 
    for (int i = 0; i < n; i++) {
        for (int j = 0; j < n; j++)
            cout << c[i][j] << " ";
        cout << endl;
    }
}

Java

// Java program for addition
// of two matrices
class GFG
{
 
  // Driver code
  public static void main(String[] args)
  {
    int n = 2, m = 2;
    int a[][] = { { 2, 5 }, { 1, 7 } };
 
    int b[][] = { { 3, 7 }, { 2, 9 } };
 
    // To store result
    int c[][] = new int[n][m];
 
    for (int i = 0; i < n; i++) {
      for (int j = 0; j < m; j++)
        c[i][j] = a[i][j] + b[i][j];
    }
 
    for (int i = 0; i < n; i++) {
      for (int j = 0; j < m; j++)
        System.out.print(c[i][j] + " ");
      System.out.print("\n");
    }
  }
}
 
// This code is contributed by Aarti_Rathi

Python3

# Python3 program for addition
# of two matrices
 
N = 4
# This function adds A[][]
# and B[][], and stores
# the result in C[][]
 
 
# driver code
a = [ [2, 5],
    [1, 7]]
 
b= [ [3, 7],
    [2, 9]]
     
N = 2
 
c=a[:][:] # To store result
 
for i in range(N):
    for j in range(N):
        c[i][j] = a[i][j] + b[i][j]
 
 
for i in range(N):
    for j in range(N):
        print(c[i][j], " ", end='')
    print()
     
# This code is contributed by Aarti_Rathi

C#

// C# program to rotate a
// matrix by 90 degrees
using System;
class GFG {
 
  // Driver Code
  static public void Main()
  {
    int N = 2;
    int M = 2;
 
    // Test Case 1
    int[,] a = { { 2, 5 }, { 1, 7 } };
    int[,] b = { { 3, 7 }, { 2, 9 } };
 
    int [,] c =new int[N,M];
    for (int i = 0; i < N; i++)
      for (int j = 0; j < M; j++) {
        c[i,j] = a[i,j] + b[i,j];
      }
 
    for (int i = 0; i < N; i++) {
      for (int j = 0; j < M; j++)
        Console.Write(c[i,j] + " ");
      Console.WriteLine();
    }
  }
}
 
// This code is contributed by Aarti_Rathi

Javascript

<script>
 
// Javascript Program for matrix addition
var n = 2, m = 2;
var a = [[ 2, 5 ], [ 1, 7 ]];
var b = [[ 3, 7 ], [ 2, 9 ]];
var c = Array.from(Array(n), ()=>Array(m).fill(0));
for (var i = 0; i < n; i++)
    for (var j = 0; j < n; j++) {
        c[i][j] = a[i][j] + b[i][j];
    }
for (var i = 0; i < n; i++) {
    for (var j = 0; j < n; j++)
        document.write( c[i][j] + " ");
    document.write("<br>");
}
 
// This code is contributed by noob2000.
</script>

Producción:

5 12 
3 16

Complejidad temporal: O(n * m)

Espacio Auxiliar: O(n * m)
Puntos clave:

  • La suma de arrays es conmutativa, lo que significa que A+B = B+A
  • La suma de arrays es asociativa, lo que significa que A+(B+C) = (A+B)+C
  • El orden de las arrays A, B y A+B es siempre el mismo
  • Si el orden de A y B es diferente, A+B no se puede calcular
  • La complejidad de la operación de suma es O(m*n) donde m*n es el orden de las arrays

Resta de arrays: 
la resta de dos arrays A m*n y B m*n da como resultado una array C m*n . Los elementos de C son la diferencia de los elementos correspondientes en A y B que se pueden representar como: 

2

El algoritmo para la resta de arrays se puede escribir como:  

for i in 1 to m
   for j in 1 to n
      cij = aij-bij

C++

// C++ Program for matrix subtraction
 
#include <iostream>
using namespace std;
 
int main()
{
 
    int n = 2, m = 2;
    int a[n][m] = { { 2, 5 }, { 1, 7 } };
    int b[n][m] = { { 3, 7 }, { 2, 9 } };
 
    int c[n][m];
    for (int i = 0; i < n; i++)
        for (int j = 0; j < n; j++) {
            c[i][j] = a[i][j] - b[i][j];
        }
 
    for (int i = 0; i < n; i++) {
        for (int j = 0; j < n; j++)
            cout << c[i][j] << " ";
        cout << endl;
    }
}

Java

public class GFG {
    // Java Program for matrix subtraction
 
    public static void main(String[] args)
    {
 
        int n = 2;
        int m = 2;
        int[][] a = { { 2, 5 }, { 1, 7 } };
        int[][] b = { { 3, 7 }, { 2, 9 } };
 
        int[][] c = new int[n][m];
        for (int i = 0; i < n; i++) {
            for (int j = 0; j < n; j++) {
                c[i][j] = a[i][j] - b[i][j];
            }
        }
 
        for (int i = 0; i < n; i++) {
            for (int j = 0; j < n; j++) {
                System.out.print(c[i][j]);
                System.out.print(" ");
            }
            System.out.print("\n");
        }
    }
}
 
// This code is contributed by Aarti_Rathi

Python3

# Python3 program for addition
# of two matrices
N = 4
 
# This function adds A[][]
# and B[][], and stores
# the result in C[][]
 
# driver code
a = [[2, 5],
     [1, 7]]
 
b = [[3, 7],
     [2, 9]]
 
N = 2
 
c = a[:][:]  # To store result
 
for i in range(N):
    for j in range(N):
        c[i][j] = a[i][j] - b[i][j]
 
 
for i in range(N):
    for j in range(N):
        print(c[i][j], " ", end='')
    print()
 
# This code is contributed by Aarti_Rathi

C#

// C# program to rotate a
// matrix by 90 degrees
using System;
  
class GFG {
  
     // Driver Code
    static public void Main()
    {
        int N = 2;
        int M = 2;
        
        // Test Case 1
        int[,] a = { { 2, 5 }, { 1, 7 } };
        int[,] b = { { 3, 7 }, { 2, 9 } };
  
        int [,] c =new int[N,M];
        for (int i = 0; i < N; i++)
            for (int j = 0; j < M; j++) {
                c[i,j] = a[i,j] - b[i,j];
            }
      
        for (int i = 0; i < N; i++) {
            for (int j = 0; j < M; j++)
                Console.Write(c[i,j] + " ");
            Console.WriteLine();
        }
    }
}
  
// This code is contributed by Aarti_Rathi

Javascript

<script>
 
// Javascript Program for matrix subtraction
var n = 2, m = 2;
var a = [[ 2, 5 ], [ 1, 7 ]];
var b = [[ 3, 7 ], [ 2, 9 ]];
var c = Array.from(Array(n), ()=>Array(m).fill(0));
for (var i = 0; i < n; i++)
    for (var j = 0; j < n; j++) {
        c[i][j] = a[i][j] - b[i][j];
    }
for (var i = 0; i < n; i++) {
    for (var j = 0; j < n; j++)
        document.write( c[i][j] + " ");
    document.write("<br>");
}
 
// This code is contributed by akshitsaxena09
</script>

Producción:

-1 -2 
-1 -2

Puntos clave:

  • La resta de arrays no es conmutativa, lo que significa AB ≠ BA
  • La resta de arrays no es asociativa, lo que significa que A-(BC) ≠ (AB)-C
  • El orden de las arrays A, B y AB es siempre el mismo
  • Si el orden de A y B es diferente, AB no se puede calcular
  • La complejidad de la operación de resta es O(m*n) donde m*n es el orden de las arrays

Multiplicación de Arrays – 
La multiplicación de dos arrays A m*n y B n*p da una array C m*p . Significa que el número de columnas en A debe ser igual al número de filas en B para calcular C=A*B. Para calcular el elemento c11, multiplique los elementos de la primera fila de A con la primera columna de B y súmelos (5*1+6*4), que se puede mostrar como: 

1

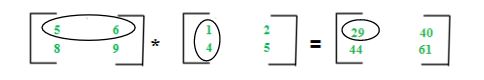
El algoritmo para la multiplicación de las arrays A de orden m*n y B de orden n*p se puede escribir como: 

for i in 1 to m
   for j in 1 to p
      cij = 0
      for k in 1 to n
         cij += aik*bkj

C++

// C++ Program for matrix Multiplication
 
#include <iostream>
using namespace std;
 
int main()
{
 
    int n = 2, m = 2;
    int a[n][m] = { { 2, 5 }, { 1, 7 } };
    int b[n][m] = { { 3, 7 }, { 2, 9 } };
 
    int c[n][m];
    int i, j, k;
    for (i = 0; i < n; i++)
    {
        for (j = 0; j < n; j++)
        {
            c[i][j] = 0;
            for (k = 0; k < n; k++)
                c[i][j] += a[i][k] * b[k][j];
        }
    }
 
    for (int i = 0; i < n; i++)
    {
        for (int j = 0; j < n; j++)
            cout << c[i][j] << " ";
        cout << endl;
    }
}

C#

// C# program to rotate a
// matrix by 90 degrees
using System;
 
class GFG {
 
  // Driver Code
  static public void Main()
  {
    int N = 2;
    int M = 2;
 
    // Test Case 1
    int[,] a = { { 2, 5 }, { 1, 7 } };
    int[,] b = { { 3, 7 }, { 2, 9 } };
 
    int [,] c =new int[N,M];
 
    for (int i = 0; i < N; i++)
    {
      for (int j = 0; j < M; j++) {
        c[i,j]=0;
        for(int k=0;k<N;k++)
          c[i,j] = c[i,j]+(a[i,k] * b[k,j]);
      }
    }
 
    for (int i = 0; i < N; i++) {
      for (int j = 0; j < M; j++)
        Console.Write(c[i,j] + " ");
      Console.WriteLine();
    }
  }
}
 
// This code is contributed by Aarti_Rathi

Javascript

<script>
 
// Javascript Program for matrix multiplication
var n = 2, m = 2;
var a = [[ 2, 5 ], [ 1, 7 ]];
var b = [[ 3, 7 ], [ 2, 9 ]];
var c = Array.from(Array(n), ()=>Array(m).fill(0));
for (var i = 0; i < n; i++){
    for (var j = 0; j < n; j++) {
        c[i][j] = 0;
        for (var k = 0; k < n; k++) {
            c[i][j] += a[i][k] * b[k][j];
    }
    }}
for (var i = 0; i < n; i++) {
    for (var j = 0; j < n; j++)
        document.write( c[i][j] + " ");
    document.write("<br>");
}
 
// This code is contributed by Sajal Aggarwal.
</script>

Producción:

16 59 
17 70

Puntos clave: 

  • La multiplicación de arrays no es conmutativa, lo que significa que A*B ≠ B*A
  • La multiplicación de arrays es asociativa, lo que significa A*(B*C) = (A*B)*C
  • Para calcular A*B, el número de columnas en A debe ser igual al número de filas en B
  • La existencia de A*B no implica la existencia de B*A
  • La complejidad de la operación de multiplicación (A*B) es O(m*n*p) donde m*n y n*p son orden de A y B respectivamente
  • El orden de la array C calculado como A*B es m*p donde m*n y n*p son el orden de A y B respectivamente

Leer a continuación: determinante de una array , adjunto e inverso de una array

Publicación traducida automáticamente

Artículo escrito por GeeksforGeeks-1 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Deja una respuesta

Tu dirección de correo electrónico no será publicada. Los campos obligatorios están marcados con *