Dipolo eléctrico

La carga eléctrica es una propiedad fundamental de la materia que controla cómo un campo eléctrico o magnético afecta a las partículas elementales. La carga eléctrica existe en unidades naturales discretas que no pueden generarse ni destruirse. Las cargas positivas y negativas son los dos tipos de cargas eléctricas. Cuando dos elementos con un exceso de un tipo de carga están lo suficientemente cerca, se repelen entre sí. Cuando dos objetos con carga positiva y carga negativa están en estrecho contacto, se atraen entre sí.

Muchas partículas fundamentales o subatómicas de la materia comparten la propiedad de la carga eléctrica. Los protones tienen carga positiva, mientras que los electrones tienen carga negativa. Los neutrones, por otro lado, no tienen carga, es decir, son partículas neutras. La carga negativa de cada electrón tiene la misma magnitud que la carga positiva de cada protón. La carga de un electrón o protón, que es una constante física fundamental, se mide en unidades naturales.

Un par de cargas puntuales iguales y opuestas q y –q separadas por una distancia 2a forman un dipolo eléctrico y el momento dipolar eléctrico (p) es el producto de la carga y el espacio entre las cargas (2a), se usa para determinar el Fuerza de un dipolo eléctrico.

Una dirección en el espacio está definida por la línea que une las dos cargas. La dirección de –q a q se conoce comúnmente como la dirección del dipolo. El centro del dipolo es la ubicación del punto medio de –q y q.

La carga total del dipolo eléctrico es definitivamente cero. Esto no implica que el campo del dipolo eléctrico sea cero. Debido a que las cargas q y –q están separadas por cierta distancia, los campos eléctricos que producen no se anulan exactamente cuando se juntan. Los campos atribuibles a q y –q casi se anulan en distancias mucho mayores que la separación de las dos cargas que producen un dipolo (r >> 2a). Como resultado, el campo eléctrico producido por un dipolo decae más rápido que 1/r ² (la dependencia del campo debido a una sola carga q en r).

Estas ideas cualitativas se confirman mediante el cálculo explícito de la siguiente manera:

El campo de un dipolo eléctrico.

La ley de Coulomb y el principio de superposición se pueden utilizar para calcular el campo eléctrico de un par de cargas (–q y q) en cualquier punto del espacio. Para los siguientes dos escenarios, los resultados son simples y claros,

Cuando el punto está en el eje del dipolo,
Cuando se encuentra en el plano ecuatorial del dipolo, es decir, en un plano perpendicular al eje del dipolo que pasa por su centro.

Aplicando la ley de vectores del paralelogramo, el campo eléctrico en cualquier punto general P se determina sumando los campos eléctricos E _–q debido a la carga –q y E _+q debido a la carga q.

Para puntos en el eje

El campo eléctrico de un dipolo en un punto del eje.

Supongamos que el punto P está a una distancia r del centro del dipolo del lado de la carga q. Entonces el campo eléctrico E _–q debido a la carga –q se puede expresar como,

$E_{-q}=-\frac{q}{4\pi\epsilon_0(r+a)^2}\hat{P}$

donde $\hat{P}$ es el vector unitario a lo largo del eje del dipolo que va de –q a q. De manera similar, entonces el campo eléctrico E _+q debido a la carga +q se puede expresar como,

$E_{+q}=\frac{q}{4\pi\epsilon_0(r-a)^2}\hat{P}$

Ahora, el campo total en P se puede calcular sumando los campos eléctricos E _–q debido a la carga –q y E _+q debido a la carga +q y se puede expresar como,

$E=E_{+q}+E_{-q}\\ E=\frac{q}{4\pi\epsilon_0(r-a)^2}\hat{P}+\left(-\frac{q}{4\pi\epsilon_0(r+a)^2}\hat{P}\right)\\ E=\frac{q}{4\pi\epsilon_0(r-a)^2}\hat{P}-\frac{q}{4\pi\epsilon_0(r+a)^2}\hat{P}\\ E=\frac{q}{4\pi\epsilon_0}\left[\frac{1}{(r-a)^2}-\frac{1}{(r+a)^2}\right]\hat{P}\\ E=\frac{q}{4\pi\epsilon_0}\frac{4ar}{(r^2-a^2)^2}\hat{P}$

Para r >> a, la expresión anterior se puede escribir como,

$E=\frac{q}{4\pi\epsilon_0}\frac{4ar}{(r^2)^2}\hat{P}\\ E=\frac{q}{4\pi\epsilon_0}\frac{4ar}{r^4}\hat{P}\\ E=\frac{q}{4\pi\epsilon_0}\frac{4a}{r^3}\hat{P}$

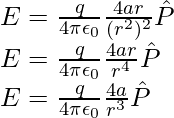
Para puntos en el plano ecuatorial

El campo eléctrico de un dipolo en un punto en el plano ecuatorial del dipolo. p es el vector de momento dipolar de magnitud p = q×2a y dirigido de –q a q.

Entonces, el campo eléctrico E _+q debido a la carga +q se puede expresar como,

$E_{+q}=\frac{q}{4\pi\epsilon_0}\frac{1}{r^2+a^2}$

De manera similar, entonces el campo eléctrico E _-q debido a la carga –q se puede expresar como,

$E_{-q}=\frac{q}{4\pi\epsilon_0}\frac{1}{r^2+a^2}$

Se observa que los campos eléctricos E _–q debido a la carga –q y E _+q debido a la carga +qy son iguales. Las direcciones E _+q y E _–q se muestran en la figura anterior. Las componentes normales al eje del dipolo se anulan claramente. A lo largo del eje del dipolo, los componentes se suman. Todo el campo eléctrico está en dirección opuesta a $\hat{P}$ .

La expresión anterior se puede agregar como,

$E=-(E_{+q}+E_{-q})\cos\theta\hat{P}\\ E=-\frac{2q}{4\pi\epsilon_0}\frac{a}{(r^2+a^2)^{3/2}}\hat{P}$

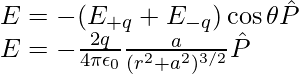
A grandes distancias (r >> a), la expresión anterior se puede escribir como,

$E=-\frac{2q}{4\pi\epsilon_0}\frac{a}{(r^2)^{3/2}}\hat{P}\\ E=-\frac{2q}{4\pi\epsilon_0}\frac{a}{r^3}\hat{P}$

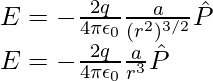
A grandes distancias, es evidente en ambos casos que el campo dipolar no involucra qya por separado; es dependiente del producto qa. Esto sugiere el significado del momento dipolar. El momento dipolar de un dipolo eléctrico es una cantidad vectorial y su símbolo es p está definido por

$p=q\times2a\hat{P}$

El campo eléctrico de un dipolo a grandes distancias (r >> a) asume formas simples en términos de p:

En un punto del eje del dipolo: $E=\frac{2p}{4\pi\epsilon_0r^3}$
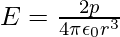
En un punto del plano ecuatorial: $E=-\frac{p}{4\pi\epsilon_0r^3}$

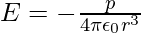
Vale la pena señalar que el campo dipolar a grandes distancias disminuye como 1/r 3 en lugar de 1/r 2. Además, la amplitud y la dirección del campo dipolar dependen no solo de la distancia r sino también del ángulo formado por el vector de posición r y el momento dipolar p.

Importancia física de los dipolos

Los centros de carga positiva y negativa se encuentran en el mismo lugar en la mayoría de las moléculas. Como resultado, su momento dipolar es nulo. CO2 y CH4 son ejemplos de esta clase de moléculas. Cuando se aplica un campo eléctrico, forman un momento dipolar. Sin embargo, los centros de cargas positivas y negativas pueden no coincidir siempre en compuestos particulares. Como resultado, incluso en ausencia de un campo eléctrico, tienen un momento dipolar eléctrico persistente. Las moléculas polares son el nombre de este tipo de moléculas. Las moléculas de H2O, por ejemplo, son un ejemplo de este tipo.

Dipolo en un archivo externo uniforme

Dipolo en un campo eléctrico uniforme.

Supongamos un dipolo permanente en un campo externo uniforme E con un momento dipolar de p. Sobre q hay una fuerza qE y sobre –q hay una fuerza –qE. Como E es uniforme, la fuerza neta sobre el dipolo es cero. Debido a la separación de las cargas, las fuerzas operan en varios lugares, provocando un momento de torsión en el dipolo. El par (par) es independiente del origen cuando la fuerza neta es cero. Su amplitud es igual a la suma de las magnitudes de las dos fuerzas antiparalelas multiplicadas por el brazo del par (distancia perpendicular entre las dos fuerzas antiparalelas). La magnitud del par se puede expresar como,

τ = q mi × 2 a senθ

o τ = 2 qa E senθ

Su dirección es perpendicular al plano del papel, saliendo de él. La magnitud de p × E también es pE senθ y su dirección es normal al papel que sale de él.

τ = = pag × mi

El dipolo tenderá a alinearse con el campo E como resultado de este par. El par es 0 cuando p está alineado con E.

Si el campo no es uniforme, la fuerza neta sin duda será mayor que cero. Además, como antes, habrá torsión en el sistema. Debido a que el caso general es complicado, considere los casos más simples cuando p es paralelo a E o antiparalelo a E. El momento de torsión neto es cero en ambos casos, pero hay una fuerza neta sobre el dipolo si E no es uniforme.

Problemas de muestra

Problema 1: Defina el término momento dipolar eléctrico de un dipolo. Indique su unidad SI.

Solución:

Un par de cargas puntuales iguales y opuestas q y –q separadas por una distancia 2a forman un dipolo eléctrico y el momento dipolar eléctrico (p) es el producto de la carga y el espacio entre las cargas (2a), se usa para determinar el Fuerza de un dipolo eléctrico. Su unidad SI es Cm.

$p=q\times2a\hat{P}$

o

|P|=q|2a|

Problema 2: ¿En qué orientación, un dipolo colocado en un campo eléctrico uniforme está en un equilibrio estable e inestable?

Solución:

Se coloca un dipolo paralelo al campo eléctrico para un equilibrio estable y un dipolo antiparalelo al campo eléctrico para un equilibrio inestable.

Si el campo no es uniforme, la fuerza neta sin duda será mayor que cero. Además, como antes, habrá torsión en el sistema. Debido a que el caso general es complicado, considere los casos más simples cuando p es paralelo a E o antiparalelo a E. El momento de torsión neto es cero en ambos casos, pero hay una fuerza neta sobre el dipolo si E no es uniforme.

Problema 3: ¿Por qué las líneas de campo eléctrico son perpendiculares en un punto sobre una superficie equipotencial de un conductor?

Solución:

Habría un componente distinto de cero a lo largo de la superficie si las líneas del campo eléctrico no fueran normales a la superficie equipotencial. Se requeriría trabajo para mover una unidad de carga de prueba contra el componente de la dirección del campo, lo que indica que esta superficie no puede ser una superficie equipotencial. Como resultado, las líneas de campo eléctrico son perpendiculares en un punto de la superficie equipotencial de un conductor.

Problema 4: Dado un campo eléctrico uniforme, encuentre el flujo de este campo a través de un cuadrado de 20 cm de lado, cuyo plano es paralelo al plano yz. ¿Cuál sería el flujo a través del mismo cuadrado, si el plano forma un ángulo de 30° con el eje x?

Solución:

Dado,

campo eléctrico es $5\times10^3\hat{i}\text{ N/C}$

A = 10 × 10 × 10 ^-4 m ² ,

Flujo (ϕ) = EA cos θ

Caso 1,

θ = 0°,

o cos 0° = 1

Por lo tanto, Flujo, ϕ= (5 × 10 ³ ) × (10 × 10 × 10 ^-4 ) cos 0°

ϕ = 50 Nm ² C ^-1

caso 2,

Ángulo del plano cuadrado con eje x = 30°

Por lo tanto, el ángulo será (90° – 30°) = 60°

ϕ = EA cos θ

ϕ = (5 × 10 ³ ) × (10 × 10 × 10 ^-4 ) × cos 60°

ϕ = 50 × 1/2

ϕ = 25 Nm ² C ^-1

Problema 5: Defina el término ‘flujo eléctrico’. Escribe sus unidades SI. ¿Cuál es el flujo debido al campo eléctrico a través de un cuadrado de lado 10 cm, cuando también se mantiene normal si?

Solución:

El número total de líneas de fuerza que se mueven a través de un área en un campo eléctrico se conoce como flujo eléctrico. Se representa con el símbolo ϕ. Es un número con un valor escalar. Su unidad SI es Nm ² C ^-1 o Vm.

Se expresa como,

$\phi=\int_{S}\overrightarrow{E}\cdot{\overrightarrow{dS}}= \frac{q}{\epsilon_0}$

Dado,

El campo eléctrico es 3×10 ³ N/C.

El área es (10/100)×(10/100) m ² = 10 ^-2 m ²

θ = 0°,

o

cos 0° = 1

La expresión para el flujo se puede escribir como,

ϕ = EA cos θ

Por lo tanto, Flujo, ϕ= (3 × 10 ³ ) × (10 ^-2 ) cos 0°

ϕ = 30 Nm ² C ^-1

Problema 6: ¿Por qué las líneas de campo eléctrico no forman lazos cerrados?

Solución:

Debido a que la dirección de un campo eléctrico es de carga positiva a negativa, no forma bucles cerrados. Como resultado, se puede considerar que una línea de fuerza comienza con una carga positiva y termina con una carga negativa.

Problema 7: ¿El campo eléctrico debido a una configuración de carga con carga total cero, es necesariamente cero? Justificar.

Solución:

No, no es necesariamente cero. Si el campo eléctrico debido a una configuración de carga con carga total es cero porque el campo eléctrico debido a un dipolo eléctrico es distinto de cero.

Publicación traducida automáticamente

Artículo escrito por anoopraj758 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA