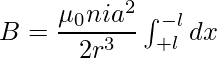Las líneas de campo magnético producidas por el imán están representadas por el patrón de limaduras de hierro. Podemos obtener una estimación aproximada del campo magnético B observando estas líneas de campo magnético. Sin embargo, con frecuencia se nos pide que midamos con precisión la magnitud del campo magnético B. Hacemos esto colocando una pequeña aguja de brújula en el campo magnético con un momento magnético my un momento de inercia conocidos y permitiéndole oscilar. ¡Echemos un vistazo más de cerca al concepto!
Un dipolo magnético suele ser un pequeño imán con dimensiones atómicas o subatómicas, similar a un flujo de carga eléctrica alrededor de un bucle. Los núcleos atómicos con carga positiva que giran, los electrones que giran sobre sus ejes y los electrones que viajan alrededor de los núcleos atómicos son todos dipolos magnéticos.
Estos efectos pueden cancelarse entre sí, dando como resultado una cierta forma de átomo que no es un dipolo magnético. El átomo es un dipolo magnético eterno si no se anulan totalmente. Los átomos de hierro, por ejemplo, son dipolos. Un dipolo magnético se forma cuando millones de átomos de hierro se unen espontáneamente en el mismo arreglo, formando un dominio ferromagnético. Los dipolos magnéticos macroscópicos incluyen cosas como agujas y barras de brújulas magnéticas.
Considere una barra magnética (NS) con una longitud de 2¼ y una fuerza polar de m en un campo magnético uniforme de inducción indicado como B creando un ángulo θ. La primera fuerza (m × B) actúa sobre el Polo Norte en la dirección del campo magnético, mientras que la segunda fuerza (m × B) actúa sobre el Polo Sur en dirección opuesta al campo magnético. Estas dos nuevas fuerzas son iguales y opuestas entre sí. Como resultado, se crea una pareja.
Par de campo uniforme en un dipolo magnético
El Polo Norte detecta una fuerza igual a la multiplicación de la intensidad del campo magnético y la fuerza del polo en la dirección del campo magnético cuando una barra magnética (que puede considerarse como un dipolo magnético) se mantiene en un campo magnético uniforme.
No obstante, el Polo Sur detecta una fuerza de dirección igual pero opuesta. Como resultado, se aplica un par de torsión al dipolo magnético, lo que hace que gire. Debido a que el par es el par, se denota por τ.
τ = Fuerza × Distancia
∴ τ = F × NA
Tenemos, F = m × B
Entonces, = mB × 2ļ sen θ = MB sen θ
en forma vectorial,
Perpendicular al plano en la dirección de τ.
Si θ = 90 o y B = 1.
Entonces, τ = MB sen θ = M
Como resultado, la inducción del momento magnético es igual al par requerido para mantener el imán a 90 grados con un campo magnético.
Análogo electrostático: compare la ecuación de un dipolo eléctrico en un campo eléctrico con la ecuación de un dipolo eléctrico en un campo magnético. El campo magnético producido por un imán de barra a gran distancia es equivalente a un dipolo eléctrico en un campo eléctrico, concluimos. De manera similar, como se muestra a continuación, la relación podría tener un estado.
mi → segundo, p → metro, 1/4πε 0 → μ 0 /4π
Si el valor de r, es decir, la distancia entre un punto y un imán en particular, es relativamente grande en comparación con el tamaño del imán proporcionado por I, o r >> l, el campo ecuatorial creado por un imán de barra puede ser Escrito como,
B mi = −μ 0 m/4πr 3
De manera similar, en la misma condición, el campo axial del imán de barra se puede expresar como,
B UNA = −μ 0 2m/4πr 3
Dipolo en un campo magnético uniforme
Un momento magnético es una medida de la fuerza y orientación magnéticas de un imán, así como del campo magnético de cualquier otro objeto. Un momento magnético se denomina con mayor precisión momento dipolar magnético, que es el componente del momento magnético que puede representarse mediante un dipolo magnético. En un dipolo magnético, dos polos norte magnéticos están separados por una pequeña distancia.
Un dipolo magnético está formado por dos polos diametralmente opuestos y separados por una pequeña distancia.
Los imanes de barra, las agujas de las brújulas y otros elementos son dipolos magnéticos. Se comparará el comportamiento de un bucle de corriente con el de un dipolo magnético. Debido a que los electrones giran alrededor del núcleo, un átomo de una sustancia magnética se comporta como un dipolo. Los polos norte y sur de un dipolo magnético (o imán) son siempre de igual fuerza y de tipo opuesto. Además, dos polos magnéticos de este tipo siempre se encuentran en pares y no se pueden separar. La longitud magnética de un imán de barra está determinada por la distancia entre sus dos polos. Es un vector que viaja del polo S al polo N de un imán, y está representado por el número 2¼.
Momento dipolar magnético = Fuerza de cualquiera de los polos × Longitud magnética
M = m(2l)
El momento dipolar magnético es una cantidad vectorial que va del polo sur al polo norte del imán, como se muestra en el diagrama.
La unidad de M es julio/tesla o amperio metro 2 . La unidad de fuerza de los polos en el SI es la Am.
Imán de barra como solenoide equivalente
Se sabe que un bucle de corriente funciona en un dipolo magnético. Todos los fenómenos magnéticos pueden explicarse en términos de corrientes circulantes, según la teoría de Ampere.
Las líneas de campo magnético de un imán de barra y un solenoide portador de corriente son notablemente similares en la figura. Como resultado, un imán de barra, como un solenoide, puede concebirse como una gran cantidad de corrientes circulantes. De la misma manera que se puede cortar un solenoide, se puede cortar un imán de barra. Se proporcionan dos solenoides más pequeños, cada uno con características magnéticas más débiles. En un bucle continuo, las líneas de campo magnético emanan de la cara de un solenoide y entran en la cara del segundo solenoide. Cuando una pequeña aguja de brújula se mueve cerca de una barra magnética y un solenoide que lleva corriente, las desviaciones de la aguja son similares en ambas circunstancias.
Para demostrar cómo un solenoide finito que transporta corriente es equivalente a un imán de barra, calcule el campo axial de un solenoide finito que transporta corriente.
En la figura, suponga: a = el radio del solenoide, 2l = longitud del solenoide con centro O, n = cantidad de vueltas del solenoide por unidad de longitud, i = la intensidad de la corriente que atravesó el solenoide
El campo magnético debe determinarse en cualquier punto P sobre el eje del solenoide, donde OP = r. Considere un pequeño solenoide con un grosor de dx y una distancia de O de x.
n dx = número de vueltas del elemento.
La magnitud del campo magnético en P debido a este elemento de corriente se puede calcular usando la Ecuación.
dB = (μ 0 ia 2 (n dx)) / (2[(rx) 2 +a 2 ] 3/2 )
Si P se encuentra a una gran distancia de O, es decir, r>>a y r>>x, entonces [(rx) 2 +a 2 ] 3/2 ≈ r 3
dB = (μ 0 ia 2 ndx) / (2r 3 )
Como rango de variación de x si de -l a +l. Como resultado, la magnitud de todo el campo de magnitud en P como resultado del solenoide que lleva corriente es
∴ B = μ 0 ni/2 × a 2 /r 3 (2l)
∴ segundo = μ 0 /4π × 2n(2l)i π un 2 /r 3
Si M es el momento magnético del solenoide, entonces
M = Número total de vueltas × corriente × área de sección transversal
METRO = n(2l) × yo × (π un 2 )
∴ B = (μ/4π)(2M/r 3 )
Así es como se expresa el campo magnético en la línea axial de una diminuta barra magnética. Como resultado, el campo axial de un solenoide finito que transporta corriente es equivalente al de una barra magnética. Como resultado, un solenoide finito que transporta corriente es equivalente a un imán de barra en términos de funcionalidad.
Energía potencial de un dipolo magnético en un campo magnético
La energía potencial de un dipolo magnético en un campo magnético es la energía que tiene el dipolo debido a su posición única en el campo. Cuando un dipolo magnético de momento M se mantiene en un ángulo θ con la dirección de un campo magnético homogéneo B, la magnitud del par que actúa sobre él es igual a
τ = MBsenθ
Como resultado del par, el dipolo se alinea en la dirección del campo. Se requiere trabajo para rotar el dipolo contra la acción del torque. Este trabajo es almacenado como energía potencial dipolar por el dipolo magnético.
Ahora se necesita una pequeña cantidad de trabajo para rotar el dipolo en un ligero ángulo dθ contra el par restaurador.
dW = τdθ = MBsenθ dθ
El trabajo total realizado al rotar el dipolo de θ 1 = θ a θ = θ 2 es
![]()
∴ W = -MB[cosθ 2 – cosθ 1 ]
∴ La energía potencial del dipolo es
U = W = -MB[cosθ 2 – cosθ 1 ]
Si θ 1 = 90 o y θ 2 = θ, entonces
U = W = -MB[cosθ – cos90 o ]
∴ U = W = -MBcosθ
∴ W = -MBcosθ
En notación vectorial,
U = -M ‘ B ‘
Casos Particulares
- Cuando θ = 90 o
Tenemos,
U = -MBcosθ
∴U = -MBcos90 o
∴ U = 0
es decir, la energía potencial de un dipolo es cero cuando es perpendicular al campo magnético.
Como resultado, lo usamos para determinar la energía potencial de un dipolo en cualquier ángulo con B.
U = -MB(cos θ 2 – cos θ 1 )
Y tome θ 1 = 90 o y θ 2 = θ.
Por lo tanto,
U = -MB(cos θ – cos 90 o )
∴U = -MBcosθ
- Cuando θ = 0 o
tenemos,
U = -MBcosθ
∴U = -MBcos0 o
∴U = -MB
Que es mínimo.
Este es el punto de equilibrio estable donde el dipolo magnético está orientado a lo largo del campo magnético y tiene el PE mínimo
- Cuando θ = 180 o
tenemos,
U = -MBcosθ
∴U = -MBcos180 o
∴ U = MB
Que es maximo.
Este es el punto de equilibrio inestable.
Problemas de muestra
Problema 1: En un campo magnético externo B = (0,2 i + 0,2 j – 0,3 k), una bobina plana de 7 m 2 de área por la que circula una corriente de 2 A en sentido contrario a las agujas del reloj está situada de forma que la normal al plano está a lo largo de la línea (3i – 5j +4k). Encuentre la energía potencial para este caso.
Solución:
Dado: A = 7 m, n = 1/√50(3 i – 5 j +4 k) ≅ 1/7(3 i – 5 j +4 k)
A = (3 yo – 5 j + 4 k) m 2
B = (0,2 i + 0,2 j – 0,3 k)T, I = 2A
Ya que,
M = AI
∴ METRO = (6 i – 10 j + 8 k) Am 2
∴ M ≅ 14Am 2
U = MB
∴ U = -[1,2 – 2 – 2,4]
∴ U = 3,2 J
Problema 2: El radio de la órbita de un electrón alrededor del núcleo en un átomo es 0,53 Ă. Si la frecuencia de revolución del electrón es 6,8 × 10 9 MHz, encuentre el momento magnético comparable.
Solución»
Dado : e = 1,6 × 10 -19 , f = 6,8 × 10 9 , r = 0,53 × 10 -10
Solución :
M = NIA = IA = Qfa
∴ M = 1,6 × 10 -19 × 6,8 × 10 9 × 10 6 × π × 0,53 × 10 -10
∴ M = 18,10 × 10 -14 Am 2
Problema 3: Escriba la fórmula para la energía potencial magnética de un dipolo magnético en un campo magnético homogéneo.
Solución:
La fórmula para la energía potencial magnética de un dipolo magnético en un campo magnético homogéneo.
U = -M’B’
dónde,
- U = Energía potencial magnética,
- M = El momento magnético del dipolo magnético,
- B = Campo magnético uniforme.
Problema 4: El electrón en un átomo de hidrógeno gira a una velocidad de 10 16 revoluciones por segundo en una órbita con un radio de 0,6 Ă. El momento magnético asociado con el movimiento orbital del electrón es
Solución :
Dado: e = 1,6 × 10 -19 , T = 1, r = 0,6 × 10 -10
Ya que,
Yo = q/T = e/T
∴ yo = 1,6 × 10 -19 × 10 16 / 1
∴ yo = 1,6 × 10 -3
M = AI
∴ METRO = 1,6 × 10 -3 × πr 2
∴ METRO = 1,6 × 10 -3 × 3,14 × (0,6 × 10 -10 ) 2
∴ M = 1,8086 × 10 -23
Problema 5: En un campo magnético externo B, un bucle de corriente circular con momento magnético M está orientado en cualquier dirección. Determine el trabajo realizado requerido para rotar la espira 30 grados alrededor de un eje perpendicular a su plano.
Solución:
El trabajo realizado para rotar la espira 30 grados alrededor de un eje perpendicular a su plano no produce cambios en el ángulo formado por el eje de la espira con la dirección del campo magnético, por lo que el trabajo realizado para rotar la espira es cero.
W = -MB[cosθ 2 – cosθ 1 ]
Problema 6: Una partícula cargada (carga q) se mueve a una velocidad constante v en un círculo de radio R. Entonces, ¿cuál es el momento magnético que la acompaña?
Solución:
Debido al movimiento en un círculo, la corriente en una trayectoria circular es proporcionada por
yo = q/T
∴ yo = qv/2πR
Como resultado, el momento magnético de la partícula es
μ = iA
∴ μ = qv/2πR × πR 2
∴ μ = qvR/2
Publicación traducida automáticamente
Artículo escrito por bhagyashrijadhav25630 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA