Diseñe un filtro de muesca IIR para eliminar el ruido de la señal usando Python

IIR significa Infinite Impulse Response. Es una de las características sorprendentes de muchos sistemas invariantes en el tiempo lineal que se distinguen por tener una respuesta de impulso h(t)/h(n) que no se vuelve cero después de algún punto, sino que continúa infinitamente . .

¿Qué es el filtro de muesca IIR?

Un filtro Notch es un filtro de parada de banda con una banda de parada muy estrecha y dos bandas de paso, en realidad atenúa/elimina en gran medida un componente de frecuencia particular de la señal de entrada mientras deja la amplitud de las otras frecuencias más o menos sin cambios.

Las especificaciones son las siguientes:  

• Genera una señal de 15 Hz corrompida con una frecuencia de línea de alimentación de 50 Hz.
• Frecuencia de muestreo: 1 kHz

Acercarse:

Paso 1: Importación de todas las bibliotecas necesarias.

from scipy import signal
import matplotlib.pyplot as plt
import numpy as np

Paso 2: Definición de las especificaciones del filtro de muesca de paso de banda IIR

# Create/view notch filter
samp_freq = 1000  # Sample frequency (Hz)
notch_freq = 50.0  # Frequency to be removed from signal (Hz)
quality_factor = 20.0  # Quality factor

Paso 3:

# Design a notch filter using signal.iirnotch
b_notch, a_notch = signal.iirnotch(notch_freq, quality_factor, samp_freq)
 
# Compute magnitude response of the designed filter
freq, h = signal.freqz(b_notch, a_notch, fs=2*np.pi)

Paso 4:

fig = plt.figure(figsize=(8, 6))
 
# Plot magnitude response of the filter
plt.plot(freq*samp_freq/(2*np.pi), 20 * np.log10(abs(h)),
         'r', label='Bandpass filter', linewidth='2')
 
plt.xlabel('Frequency [Hz]', fontsize=20)
plt.ylabel('Magnitude [dB]', fontsize=20)
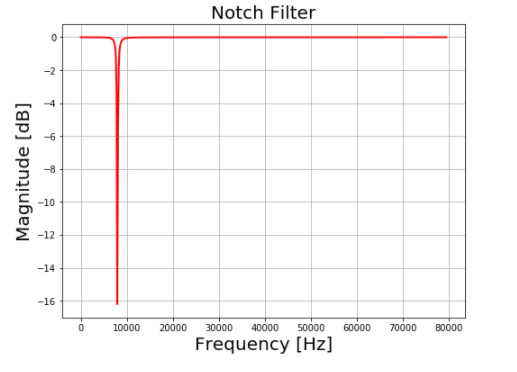
plt.title('Notch Filter', fontsize=20)
plt.grid()

Producción:

Paso 5:

# Create and view signal that is a mixture
# of two different frequencies
f1 = 15  # Frequency of 1st signal in Hz
f2 = 50  # Frequency of 2nd signal in Hz
 
# Set time vector
# Generate 1000 sample sequence in 1 sec
n = np.linspace(0, 1, 1000)

Paso 6:

# Generate the signal containing f1 and f2
noisySignal = np.sin(2*np.pi*15*n) + np.sin(2*np.pi*50*n) + \
    np.random.normal(0, .1, 1000)*0.03

Paso 7:

# Plotting
fig = plt.figure(figsize=(8, 6))
plt.subplot(211)
plt.plot(n, noisySignal, color='r', linewidth=2)
plt.xlabel('Time', fontsize=20)
plt.ylabel('Magnitude', fontsize=18)
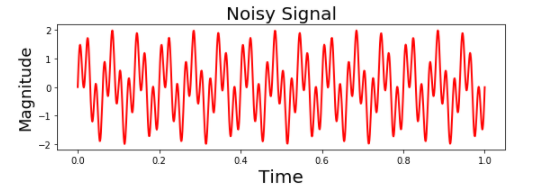
plt.title('Noisy Signal', fontsize=20)

Producción:

Paso 8:

# Apply notch filter to the noisy signal using signal.filtfilt
outputSignal = signal.filtfilt(b_notch, a_notch, noisySignal)

Paso 9:

# Plot notch-filtered version of signal
plt.subplot(212)
 
# Plot output signal of notch filter
plt.plot(n, outputSignal)
plt.xlabel('Time', fontsize=20)
plt.ylabel('Magnitude', fontsize=18)
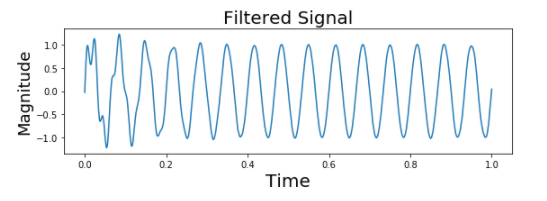
plt.title('Filtered Signal', fontsize=20)
plt.subplots_adjust(hspace=0.5)
fig.tight_layout()
plt.show()

Producción:

A continuación se muestra la implementación:

from scipy import signal
import matplotlib.pyplot as plt
import numpy as np
 
# Create/view notch filter
samp_freq = 1000  # Sample frequency (Hz)
notch_freq = 50.0  # Frequency to be removed from signal (Hz)
quality_factor = 20.0  # Quality factor
 
# Design a notch filter using signal.iirnotch
b_notch, a_notch = signal.iirnotch(notch_freq, quality_factor, samp_freq)
 
# Compute magnitude response of the designed filter
freq, h = signal.freqz(b_notch, a_notch, fs=samp_freq)
 
fig = plt.figure(figsize=(8, 6))
 
# Plot magnitude response of the filter
plt.plot(freq*samp_freq/(2*np.pi), 20 * np.log10(abs(h)),
         'r', label='Bandpass filter', linewidth='2')
plt.xlabel('Frequency [Hz]', fontsize=20)
plt.ylabel('Magnitude [dB]', fontsize=20)
plt.title('Notch Filter', fontsize=20)
plt.grid()
 
# Create and view signal that is a mixture of two different frequencies
f1 = 15  # Frequency of 1st signal in Hz
f2 = 50  # Frequency of 2nd signal in Hz
# Set time vector
n = np.linspace(0, 1, 1000)  # Generate 1000 sample sequence in 1 sec
 
# Generate the signal containing f1 and f2
noisySignal = np.sin(2*np.pi*15*n) + np.sin(2*np.pi*50*n) + \
    np.random.normal(0, .1, 1000)*0.03
 
# Plotting
fig = plt.figure(figsize=(8, 6))
plt.subplot(211)
plt.plot(n, noisySignal, color='r', linewidth=2)
plt.xlabel('Time', fontsize=20)
plt.ylabel('Magnitude', fontsize=18)
plt.title('Noisy Signal', fontsize=20)
 
# Apply notch filter to the noisy signal using signal.filtfilt
outputSignal = signal.filtfilt(b_notch, a_notch, noisySignal)
 
# Plot notch-filtered version of signal
plt.subplot(212)
 
# Plot output signal of notch filter
plt.plot(n, outputSignal)
plt.xlabel('Time', fontsize=20)
plt.ylabel('Magnitude', fontsize=18)
plt.title('Filtered Signal', fontsize=20)
plt.subplots_adjust(hspace=0.5)
fig.tight_layout()
plt.show()

Producción: