En el juego Ball Sort Puzzle , tenemos p bolas de cada color y n colores diferentes, para un total de p×n bolas, dispuestas en n pilas. Además, tenemos 2 pilas vacías. Un máximo de p bolas puede estar en cualquier pila en un momento dado. El objetivo del juego es ordenar las bolas por color en cada una de las n pilas.
Normas:
- Solo se puede mover la bola superior de cada pila.
- Una bola se puede mover encima de otra bola del mismo color.
- Una bola se puede mover en una pila vacía.
Consulte el siguiente GIF para ver un ejemplo de juego (Nivel 7):
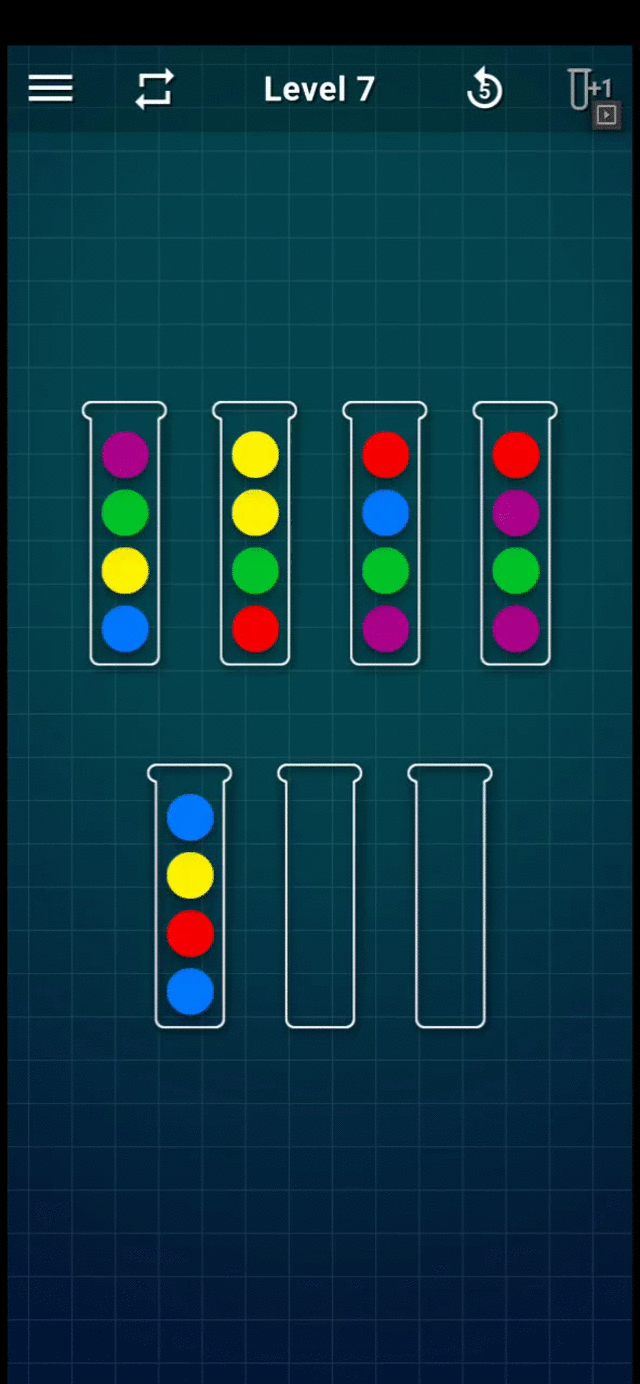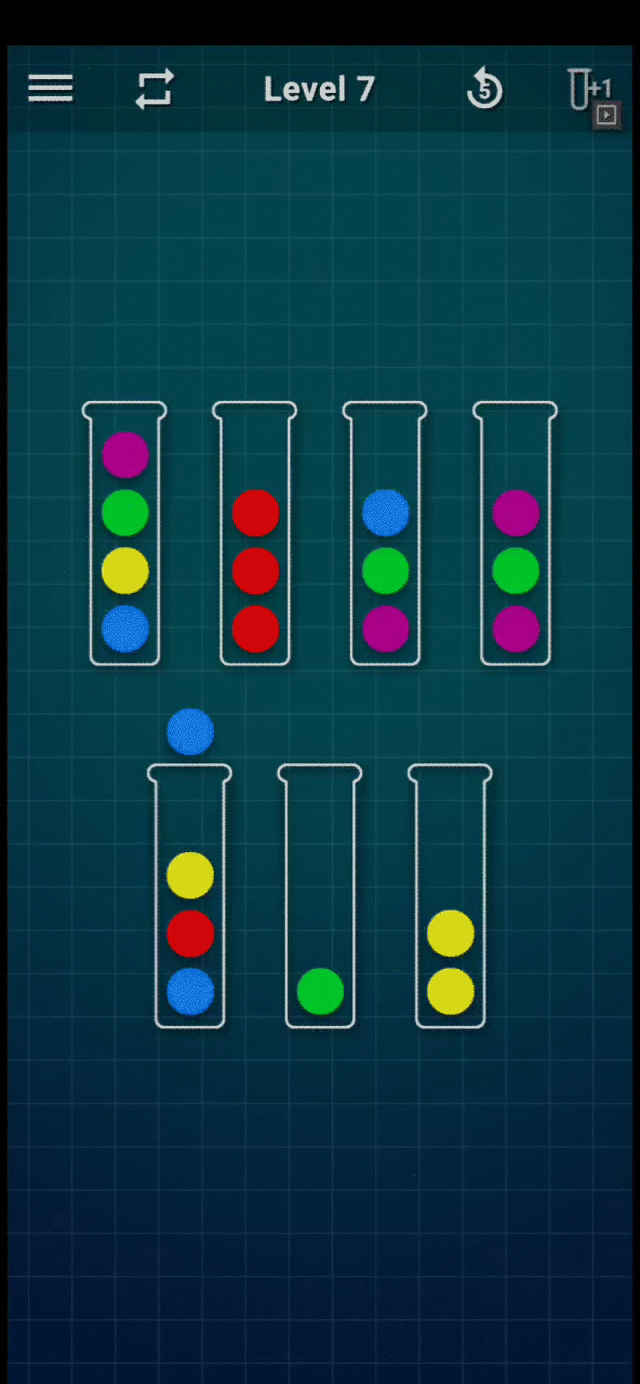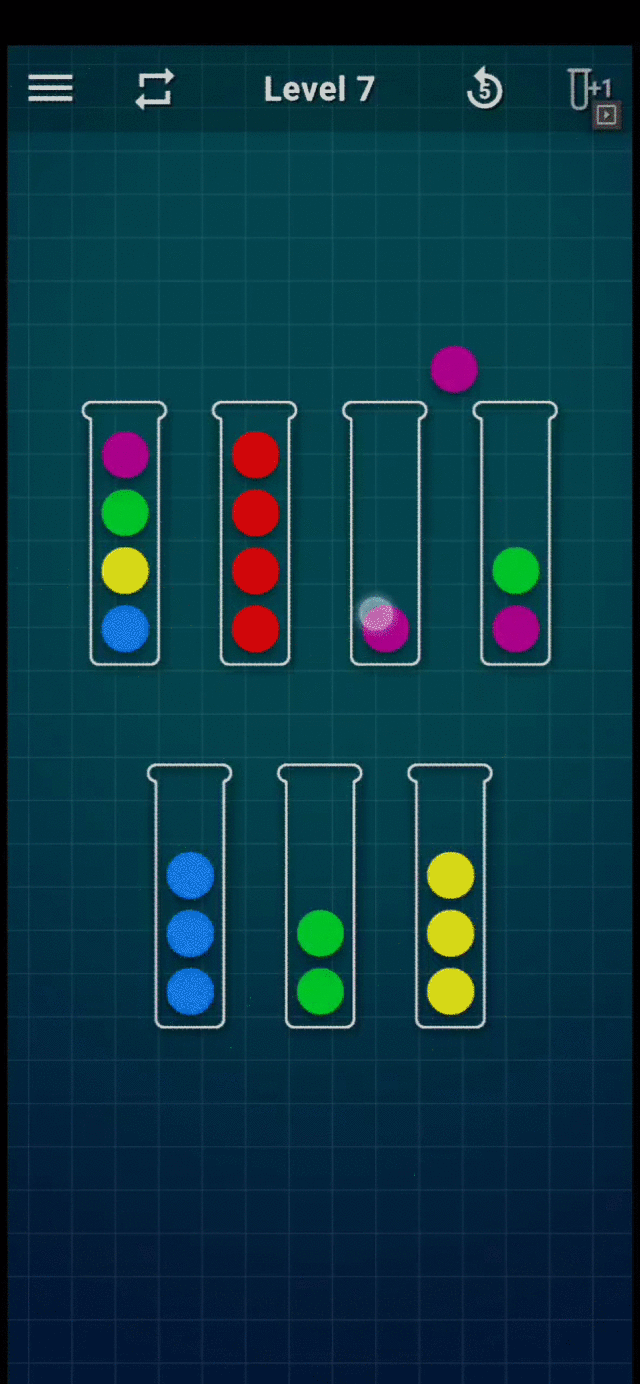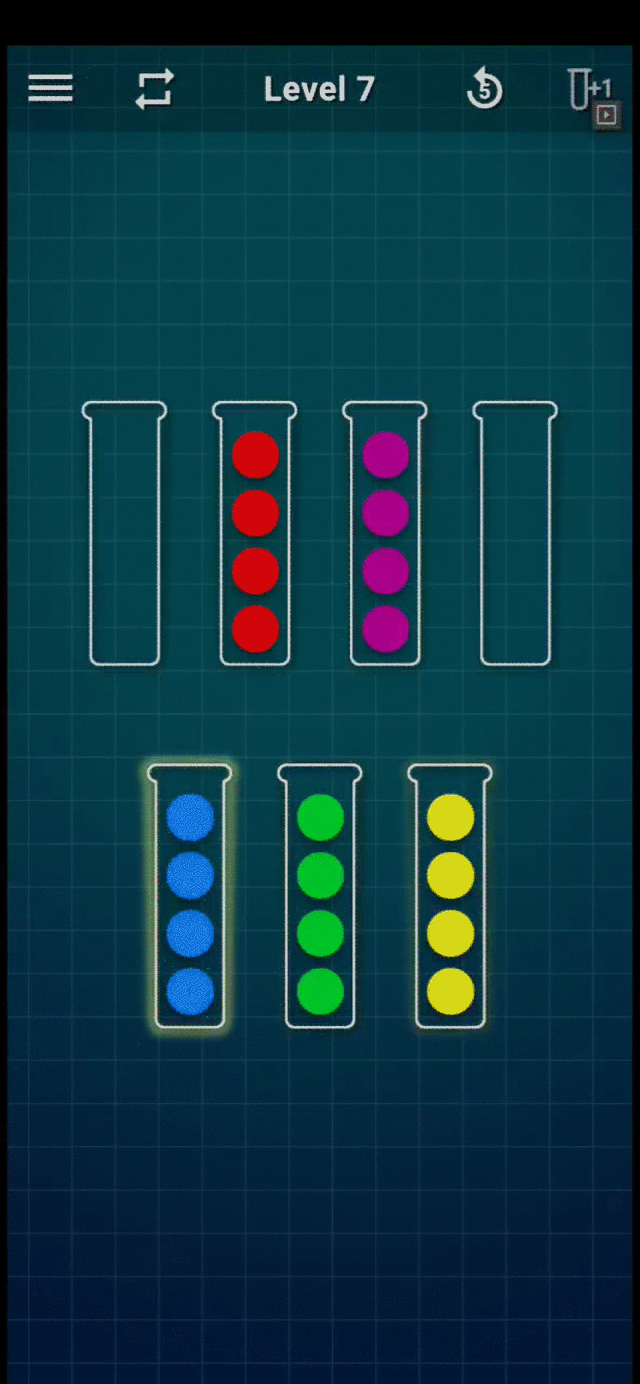
Juego de nivel 7
Enfoque I [Recursión y BackTrack]:
- A partir de las reglas dadas, se podría generar un algoritmo recursivo simple como el siguiente:
- Comience con la posición inicial dada de todas las bolas.
- Cree una cola vacía inicial.
- círculo:
- Si la posición actual está ordenada:
- devolver
- más
- Pon en cola todos los movimientos posibles en una cola.
- Quite el siguiente movimiento de la Cola.
- Ir al bucle.
- Si la posición actual está ordenada:
Sin embargo, el enfoque parece simple y correcto, tiene algunas advertencias:
- Incorrecto:
- Podríamos terminar en un ciclo infinito si hay >1 movimientos en la Cola que conducen a la misma posición de las bolas.
- Ineficiente:
- Podríamos terminar visitando la misma posición varias veces.
Por lo tanto, eliminar los cuellos de botella mencionados anteriormente resolvería el problema.
Enfoque II [Memoización usando HashMap]:
- Suposiciones:
- Representaremos las posiciones de las bolas como un vector de strings: {“gbbb”, “ybry”, “yggy”, “rrrg”}
- Cree un conjunto llamado Visitado de <String> que contendrá las posiciones visitadas como una string larga.
- Cree un vector vacío para Respuesta que almacenará las posiciones <a, b> de los tubos para mover la bola superior del tubo a y colocarla en el tubo b.
- Inicialice la cuadrícula con la configuración inicial de las bolas.
- solucionador de funciones ( cuadrícula ):
- agregar cuadrícula a Visitado
- bucle sobre todas las pilas ( i ):
- bucle sobre todas las pilas ( j ):
- Si move i -> j es válido, cree newGrid con ese movimiento.
- si las bolas están ordenadas en newGrid ,
- Actualizar respuesta ;
- devolver;
- si newGrid NO está en Visitado
- solucionador( nuevaCuadrícula )
- si se resuelve:
- Actualizar respuesta
- si las bolas están ordenadas en newGrid ,
- Si move i -> j es válido, cree newGrid con ese movimiento.
- bucle sobre todas las pilas ( j ):
Entrada de juego de muestra I:
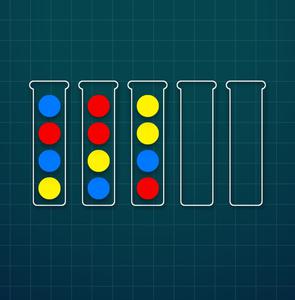
Nivel 3
Ejemplo de entrada I:
5 ybrb byrr rbyy
Salida de muestra I:
Move 1 to 4 1 times Move 1 to 5 1 times Move 1 to 4 1 times Move 2 to 5 2 times Move 1 to 2 1 times Move 3 to 1 1 times Move 1 to 2 1 times Move 3 to 1 1 times Move 2 to 1 3 times Move 2 to 3 1 times Move 3 to 4 1 times Move 3 to 2 1 times Move 2 to 4 1 times Move 3 to 5 1 times
Ejemplo de entrada de juego II:
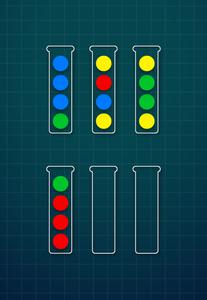
Nivel 5
Ejemplo de entrada II:
6 gbbb ybry yggy rrrg
Ejemplo de salida II:
Move 1 to 5 3 times Move 2 to 6 1 times Move 3 to 6 1 times Move 1 to 3 1 times Move 2 to 1 1 times Move 2 to 5 1 times Move 2 to 6 1 times Move 3 to 2 3 times Move 3 to 6 1 times Move 4 to 2 1 times Move 1 to 4 1 times
Consulte la siguiente implementación de C++ con los comentarios para la referencia:
C++
// C++ program for the above approach
#include <bits/stdc++.h>
using namespace std;
using Grid = vector<string>;
Grid configureGrid(string stacks[], int numberOfStacks)
{
Grid grid;
for (int i = 0; i < numberOfStacks; i++)
grid.push_back(stacks[i]);
return grid;
}
// Function to find the max
int getStackHeight(Grid grid)
{
int max = 0;
for (auto stack : grid)
if (max < stack.size())
max = stack.size();
return max;
}
// Convert vector of strings to
// canonicalRepresentation of strings
string canonicalStringConversion(Grid grid)
{
string finalString;
sort(grid.begin(), grid.end());
for (auto stack : grid) {
finalString += (stack + ";");
}
return finalString;
}
// Function to check if it is solved
// or not
bool isSolved(Grid grid, int stackHeight)
{
for (auto stack : grid) {
if (!stack.size())
continue;
else if (stack.size() < stackHeight)
return false;
else if (std::count(stack.begin(),
stack.end(),
stack[0])
!= stackHeight)
return false;
}
return true;
}
// Check if the move is valid
bool isValidMove(string sourceStack,
string destinationStack,
int height)
{
// Can't move from an empty stack
// or to a FULL STACK
if (sourceStack.size() == 0
|| destinationStack.size() == height)
return false;
int colorFreqs
= std::count(sourceStack.begin(),
sourceStack.end(),
sourceStack[0]);
// If the source stack is same colored,
// don't touch it
if (colorFreqs == height)
return false;
if (destinationStack.size() == 0) {
// If source stack has only
// same colored balls,
// don't touch it
if (colorFreqs == sourceStack.size())
return false;
return true;
}
return (
sourceStack[sourceStack.size() - 1]
== destinationStack[destinationStack.size() - 1]);
}
// Function to solve the puzzle
bool solvePuzzle(Grid grid, int stackHeight,
unordered_set<string>& visited,
vector<vector<int> >& answerMod)
{
if (stackHeight == -1) {
stackHeight = getStackHeight(grid);
}
visited.insert(
canonicalStringConversion(grid));
for (int i = 0; i < grid.size(); i++) {
// Iterate over all the stacks
string sourceStack = grid[i];
for (int j = 0; j < grid.size(); j++) {
if (i == j)
continue;
string destinationStack = grid[j];
if (isValidMove(sourceStack,
destinationStack,
stackHeight)) {
// Creating a new Grid
// with the valid move
Grid newGrid(grid);
// Adding the ball
newGrid[j].push_back(newGrid[i].back());
// Adding the ball
newGrid[i].pop_back();
if (isSolved(newGrid, stackHeight)) {
answerMod.push_back(
vector<int>{ i, j, 1 });
return true;
}
if (visited.find(
canonicalStringConversion(newGrid))
== visited.end()) {
bool solveForTheRest
= solvePuzzle(newGrid, stackHeight,
visited, answerMod);
if (solveForTheRest) {
vector<int> lastMove
= answerMod[answerMod.size()
- 1];
// Optimisation - Concatenating
// consecutive moves of the same
// ball
if (lastMove[0] == i
&& lastMove[1] == j)
answerMod[answerMod.size() - 1]
[2]++;
else
answerMod.push_back(
vector<int>{ i, j, 1 });
return true;
}
}
}
}
}
return false;
}
// Checks whether the grid is valid or not
bool checkGrid(Grid grid)
{
int numberOfStacks = grid.size();
int stackHeight = getStackHeight(grid);
int numBallsExpected
= ((numberOfStacks - 2) * stackHeight);
// Cause 2 empty stacks
int numBalls = 0;
for (auto i : grid)
numBalls += i.size();
if (numBalls != numBallsExpected) {
cout << "Grid has incorrect # of balls"
<< endl;
return false;
}
map<char, int> ballColorFrequency;
for (auto stack : grid)
for (auto ball : stack)
if (ballColorFrequency.find(ball)
!= ballColorFrequency.end())
ballColorFrequency[ball] += 1;
else
ballColorFrequency[ball] = 1;
for (auto ballColor : ballColorFrequency) {
if (ballColor.second != getStackHeight(grid)) {
cout << "Color " << ballColor.first
<< " is not " << getStackHeight(grid)
<< endl;
return false;
}
}
return true;
}
// Driver Code
int main(void)
{
// Including 2 empty stacks
int numberOfStacks = 6;
std::string stacks[]
= { "gbbb", "ybry", "yggy", "rrrg", "", "" };
Grid grid = configureGrid(
stacks, numberOfStacks);
if (!checkGrid(grid)) {
cout << "Invalid Grid" << endl;
return 1;
}
if (isSolved(grid, getStackHeight(grid))) {
cout << "Problem is already solved"
<< endl;
return 0;
}
unordered_set<string> visited;
vector<vector<int> > answerMod;
// Solve the puzzle instance
solvePuzzle(grid, getStackHeight(grid),
visited,
answerMod);
// Since the values of Answers are appended
// When the problem was completely
// solved and backwards from there
reverse(answerMod.begin(), answerMod.end());
for (auto v : answerMod) {
cout << "Move " << v[0] + 1
<< " to " << v[1] + 1
<< " " << v[2] << " times"
<< endl;
}
return 0;
}
Move 1 to 5 3 times Move 2 to 6 1 times Move 3 to 6 1 times Move 1 to 3 1 times Move 2 to 1 1 times Move 2 to 5 1 times Move 2 to 6 1 times Move 3 to 2 3 times Move 3 to 6 1 times Move 4 to 2 1 times Move 1 to 4 1 times
Publicación traducida automáticamente
Artículo escrito por Harsh Parikh y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA