Diseño de autómatas finitos a partir de expresiones regulares (Conjunto 1)

En este artículo, veremos algunas expresiones regulares populares y cómo podemos convertirlas en autómatas finitos.

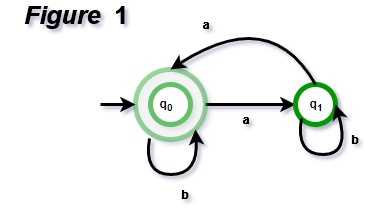
• Número par de a: la expresión regular para un número par de a es (b|ab*ab*)* . Podemos construir un autómata finito como se muestra en la Figura 1.

  

  Los autómatas anteriores aceptarán todas las strings que tengan un número par de a. Para cero a, estará en q0, que es el estado final. Para una ‘a’, irá de q0 a q1 y no se aceptará la string. Para dos a en cualquier posición, irá de q0 a q1 para la primera ‘a’ y de q1 a q0 para la segunda ‘a’. Por lo tanto, aceptará todas las strings con un número par de a.

• String con ‘ab’ como substring: La expresión regular para strings con ‘ab’ como substring es (a|b)*ab(a|b)* . Podemos construir autómatas finitos como se muestra en la Figura 2.

  

  Los autómatas anteriores aceptarán todas las strings que tengan ‘ab’ como substring. Los autómatas permanecerán en el estado inicial q0 durante b’s. Se moverá a q1 después de leer ‘a’ y permanecerá en el mismo estado para todos los ‘a’ después. Luego se moverá a q2 si se lee ‘b’. Eso significa que la string ha leído ‘ab’ como substring si llega a q2.

• String con recuento de ‘a’ divisible por 3: La expresión regular para strings con recuento de a divisible por 3 es {a ³ⁿ | n >= 0}. Podemos construir autómatas como se muestra en la Figura 3.

  

  Los autómatas anteriores aceptarán todas las strings de forma ³ⁿ . Los autómatas permanecerán en el estado inicial q0 durante ɛ y será aceptado. Para la string ‘aaa’, se moverá de q0 a q1, luego de q1 a q2 y luego de q2 a q0. Para cada conjunto de tres a, llegará a q0, por lo que se acepta. De lo contrario, estará en q1 o q2, por lo que será rechazado.

  Nota: si queremos diseñar un autómata finito con un número de a de 3n+1, se pueden usar los mismos autómatas con el estado final q1 en lugar de q0.
  Si queremos diseñar un autómata finito con lenguaje {a ^kn | n >= 0}, se requieren k estados. Hemos usado k = 3 en nuestro ejemplo.

• Números binarios divisibles por 3: La expresión regular para números binarios que son divisibles por tres es (0|1(01*0)*1)* . Los ejemplos de número binario divisible por 3 son 0, 011, 110, 1001, 1100, 1111, 10010 etc. El DFA correspondiente al número binario divisible por 3 se puede mostrar en la Figura 4.

  

  Los autómatas anteriores aceptarán todos los números binarios divisibles por 3. Para 1001, los autómatas irán de q0 a q1, luego de q1 a q2, luego de q2 a q1 y finalmente de q2 a q0, por lo tanto aceptado. Para 0111, los autómatas pasarán de q0 a q0, luego de q0 a q1, luego de q1 a q0 y finalmente de q0 a q1, por lo tanto rechazados.

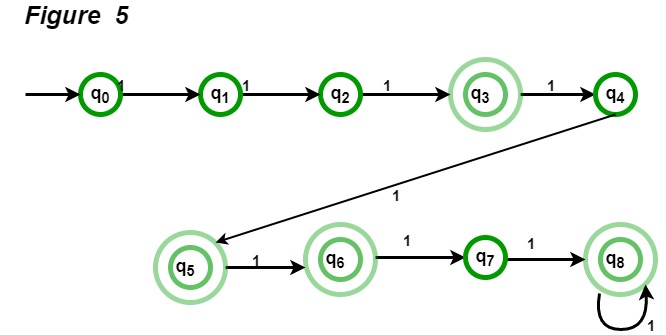
• String con expresión regular (111 + 11111)*: La string aceptada usando esta expresión regular tendrá 3, 5, 6 (111 dos veces), 8 (11111 una vez y 111 una vez), 9 (111 tres veces), 10 (11111 dos veces) y todas las demás cuentas de 1 después. El DFA correspondiente a la expresión regular dada se muestra en la Figura 5.

  

 
Pregunta: ¿Cuál será el número mínimo de estados para strings con un número impar de a?
Solución: La expresión regular para el número impar de a es b*ab*(ab*ab*)* y los autómatas correspondientes se dan en la Figura 6 y el número mínimo de estados es 2.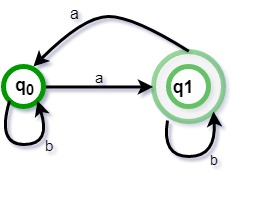

TOC | Diseño de autómatas finitos deterministas (Conjunto 1)

 
Este artículo ha sido aportado por Sonal Tuteja.
 
Escriba comentarios si encuentra algo incorrecto o si desea compartir más información sobre el tema tratado anteriormente.