Diseño de autómatas finitos deterministas (Conjunto 1) – Part 1

Requisito previo: diseño de autómatas finitos En este artículo, veremos algunos diseños de autómatas finitos deterministas (DFA). 

Problema 1: construcción de un DFA para el conjunto de strings sobre {a, b} tal que la longitud de la string |w|=2, es decir, la longitud de la string es exactamente 2. Explicación: el idioma deseado será como:

L = {aa, ab, ba, bb} 

El diagrama de transición de estado del lenguaje será como: 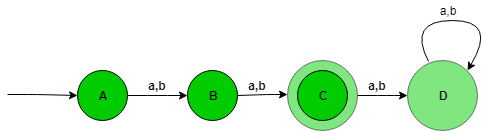Aquí, el estado A representa el conjunto de todas las strings de longitud cero (0), el estado B representa el conjunto de todas las strings de longitud uno (1), el estado C representa el conjunto de todas las strings de longitud dos (2). El estado C es el estado final y D es el estado muerto, es así porque después de obtener cualquier alfabeto como entrada, nunca pasará al estado final.

Number of states: n+2
Where n is |w|=n 

Los autómatas anteriores aceptarán todas las strings que tengan la longitud de la string exactamente 2. Cuando la longitud de la string sea 1, pasará del estado A al B. Cuando la longitud de la string sea 2, pasará de estado B a C y cuando la longitud de la string es mayor que 2, entonces pasará del estado C al D (estado muerto) y luego del estado D AL D mismo. 

#check string in
#in state A
def checkStateA(n):
     
    #if length of
    #string is one
    #print not accepted
    if(len(n)==1):
        print("string not accepted")
    else:  
        #pass string to stateB to
        #to check further transitions
        if(n[0]=='a' or n[0]=='b'):
            stateB(n[1:])
             
             
def stateB(n):
    #here if length
    #is not 1 print#string not accepted
    if(len(n)!=1):
        print("string not accepted")
    else:
        #else pass string
        #to state c
        stateC(n[1:])
def stateC(n):
    #here if length
    #becomes zero
    #print accepted
    #else not accepted
    if (len(n)==0):
        print("string accepted")
    else:
        print("string not accepted")
     
     
#take input   
n=input()
checkStateA(n)

Problema 2: construcción de un DFA para el conjunto de strings sobre {a, b} tal que la longitud de la string |w|>=2, es decir, la longitud de la string debe ser al menos 2. Explicación: el idioma deseado será me gusta:

L = {aa, ab, ba, bb, aaa, aab, aba, abb........} 

El diagrama de transición de estado del lenguaje será como: Aquí, el Estado A representa el conjunto de todas las strings de longitud cero (0), el estado B representa el conjunto de todas las strings de longitud uno (1), y el estado C representa el conjunto de todas las strings de longitud dos (2).

Number of states: n+1
Where n is |w|>=n 

Los autómatas anteriores aceptarán todas las strings que tengan una longitud de string de al menos 2. Cuando la longitud de la string sea 1, pasará del estado A al B. Cuando la longitud de la string sea 2, irá del estado B al C y, por último, cuando la longitud de la string es mayor que 2, entonces pasará del estado C al propio C. 

#check string in
#in state A
def checkStateA(n):
     
    #if length of
    #string is one
    #print not accepted
    if(len(n)==1):
        print("string not accepted")
    else:  
        #pass string to stateB to
        #to check further transitions
        if(n[0]=='a' or n[0]=='b'):
            stateB(n[1:])
             
             
def stateB(n):
     
    #here if length
    #is less than 1
    #printstring not accepted
    if(len(n)<1):
        print("string not accepted")
    else:
         
        #else pass string
        #to state c
        stateC(n[1:])
         
         
def stateC(n):
    #here if length of string
    #is greater than equal to zero
    #print accepted
    #else not accepted
    if (len(n)>=0):
        print("string accepted")
    else:
        print("string not accepted")
     
     
#take input   
n=input()
checkStateA(n)

Problema 3: construcción de un DFA para el conjunto de strings sobre {a, b} tal que la longitud de la string |w|<=2, es decir, la longitud de la string es como máximo 2.
Explicación: el idioma deseado será como:

L = {?, aa, ab, ba, bb} 

El diagrama de transición de estado del lenguaje será como: 

Aquí, el estado A representa el conjunto de todas las strings de longitud cero (0), el estado B representa el conjunto de todas las strings de longitud uno (1), el estado C representa el conjunto de todas las strings de longitud dos (2), el estado A, B, C es el estado final y D es el estado muerto, es así porque después de obtener cualquier alfabeto como entrada, nunca pasará al estado final.

Number of states: n+2
Where n is |w|<=n 

Los autómatas anteriores aceptarán todas las strings que tengan una longitud máxima de 2. Cuando la longitud de la string sea 1, pasará del estado A al B. Cuando la longitud de la string sea 2, irá del estado B al C y, por último, cuando la longitud de la string es mayor que 2, pasará del estado C al D (estado muerto). 

#check string in
#in state A
def checkStateA(n):
     
    #if only two transition occurs
    #then print string accepted
   
    if(n[0]=='a' or n[0]=='b'):
        stateB(n[1:])
             
             
def stateB(n):
     
    #if length is 0
    #print accepted
    if(len(n)==0):
        print("string accepted")
    else:
        stateC(n[1:])
         
         
def stateC(n):
    #if length is 0
    #print accepted
    #else not accepted
    if (len(n)==0):
        print("string accepted")
    else:
        print("string not accepted")
     
     
#take input   
n=input()
checkStateA(n)