Requisito previo: diseño de autómatas finitos , artículo anterior: Diseño de autómatas finitos deterministas (conjunto 1)
En este artículo, veremos algunos diseños de autómatas finitos deterministas (DFA).
Problema-1: Construcción de un DFA para el conjunto de strings sobre {a, b} tal que la longitud de la string |w| es divisible por 2, es decir, |w| módulo 2 = 0.
Explicación: el idioma deseado será como:
L = {?, aa, ab, ba, bb, aaaa, bbbb, ............}
El diagrama de transición de estado del lenguaje será como:
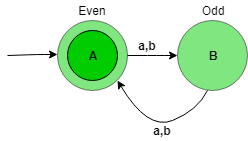
Here, state A represent set of all string of length even (0, 2, 4, …), and state B represent set of all string of length odd (1, 3, 5, …).
Number of states: n If |W| mod n = 0
def stateA(n):
if(len(n)==0):
print("Accepted")
else:
#on any input call function stateB
if (n[0]=='0' or n[0]=='1'):
stateB(n[1:])
def stateB(n):
if(len(n)==0):
print("Not Accepted")
else:
#on any input call function stateA
if (n[0]=='0' or n[0]=='1'):
stateA(n[1:])
#take input
n=input()
#call stateA
#to check the input
stateA(n)
Los autómatas anteriores aceptarán todas las strings que tengan la longitud de la string divisible por 2. Cuando la longitud de la string sea 1, irá del estado A al B. Cuando la longitud de la string sea 2, irá del estado B al A y así sucesivamente. El estado A es el estado final, es decir, acepta toda la string que tiene una longitud divisible por 2.
Problema-2: Construcción de un DFA para el conjunto de strings sobre {a, b} tal que la longitud de la string |w| no es divisible por 2, es decir, |w| módulo 2 = 1.
Explicación: el idioma deseado será como:
L = {a, b, aaa, aab, aba, abb, aaaaa, bbbb, .......}
El diagrama de transición de estado del lenguaje será como:
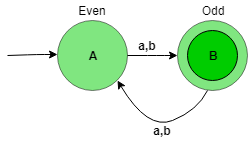
Here, state A represent set of all string of length even (0, 2, 4, …), and state B represent set of all string of length odd (1, 3, 5, …).
def stateA(n):
if(len(n)==0):
print("Not Accepted")
else:
#on any input call function stateB
if (n[0]=='0' or n[0]=='1'):
stateB(n[1:])
def stateB(n):
if(len(n)==0):
print("Accepted")
else:
#on any input call function stateA
if (n[0]=='0' or n[0]=='1'):
stateA(n[1:])
#take input
n=input()
#call stateA
#to check the input
stateA(n)
Los autómatas anteriores aceptarán todas las strings cuya longitud no sea divisible por 2. Cuando la longitud de la string sea 1, pasará del estado A al B. Cuando la longitud de la string sea 2, entonces pasar del estado B al A y así sucesivamente. El estado B es el estado final, es decir, acepta toda la string que tenga una longitud no divisible por 2.
Problema-3: Construcción de un DFA para el conjunto de strings sobre {a, b} tal que la longitud de la string |w| es divisible por 3, es decir, |w| módulo 3 = 0.
Explicación: el idioma deseado será como:
L = {?, aaa, aab, aba, abb, aaaaaa, bbbbbb, .......}
El diagrama de transición de estado del lenguaje será como:
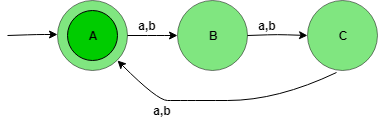
Here, state A represents set for which string’s length divided by 3 then remainder is zero (0), state B represents set for which string’s length divided by 3 then the remainder is one (1), and state C represents set for which string’s length divided by 3 then the remainder is two (2).
Number of states: n If |W| mod n = 0
def stateA(n):
if(len(n)==0):
print("Accepted")
else:
#on any input call function stateB
if (n[0]=='0' or n[0]=='1'):
stateB(n[1:])
def stateB(n):
if(len(n)==0):
print("Not Accepted")
else:
#on any input call function stateC
if (n[0]=='0' or n[0]=='1'):
stateC(n[1:])
def stateC(n):
if(len(n)==0):
print("Not Accepted")
else:
#on any input call function stateA
if (n[0]=='0' or n[0]=='1'):
stateA(n[1:])
#take input
n=input()
#call stateA
#to check the input
stateA(n)
Los autómatas anteriores aceptarán todas las strings cuya longitud sea divisible por 3. Cuando la longitud de la string sea 1, pasará del estado A al B. Cuando la longitud de la string sea 2, irá del estado B al C y cuando la longitud de la string es 3, entonces irá del estado C al A (estado final). El estado A es el estado final, es decir, acepta toda la string que tenga una longitud divisible por 3.
Problema-4: Construcción de un DFA para el conjunto de strings sobre {a, b} tal que la longitud de la string |w| no es divisible por 3, es decir, |w| módulo 3 = 1.
Explicación: el idioma deseado será como:
L = {a, b, aa, ab, ba, bb, aaaa, bbbb, ........}
El diagrama de transición de estado del lenguaje será como:
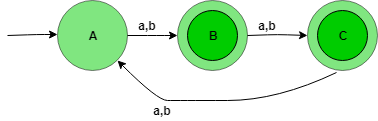
Here, state A represents set for which string’s length divided by 3 then remainder is zero (0), state B represents set for which string’s length divided by 3 then the remainder is one (1), and state C represents set for which string’s length divided by 3 then the remainder is two (2).
def stateA(n):
if(len(n)==0):
print("Not Accepted")
else:
#on any input call function stateB
if (n[0]=='0' or n[0]=='1'):
stateB(n[1:])
def stateB(n):
if(len(n)==0):
print("Accepted")
else:
#on any input call function stateC
if (n[0]=='0' or n[0]=='1'):
stateC(n[1:])
def stateC(n):
if(len(n)==0):
print("Not Accepted")
else:
#on any input call function stateA
if (n[0]=='0' or n[0]=='1'):
stateA(n[1:])
#take input
n=input()
#call stateA
#to check the input
stateA(n)
Los autómatas anteriores aceptarán todas las strings cuya longitud no sea divisible por 3. Cuando la longitud de la string sea 1, pasará del estado A al B. Cuando la longitud de la string sea 2, entonces ir del estado B al C y cuando la longitud de la string es 3, entonces irá del estado C al A. Los estados B y C son el estado final, es decir, acepta toda la string que tenga una longitud no divisible por 3.
Publicación traducida automáticamente
Artículo escrito por Kanchan_Ray y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA