Requisito previo: diseño de autómatas finitos
En este artículo, veremos algunos diseños de autómatas finitos deterministas (DFA).
Problema-1: Construcción de un DFA mínimo que acepte un conjunto de strings sobre {a, b} en las que {abwa / wε{a, b}*}.
Aquí ‘w’ es la substring que contiene alfabetos sobre cualquier número de ‘a’ y ‘b’ que van desde cero hasta el infinito.
Explicación: El idioma deseado será como:
L1 = {abεa, abaaaa, ababaaa, abaabbaaa}
Aquí, como podemos ver, cada string del idioma anterior tiene una substring inicial constante, es decir, {ab} y {a} final, pero ‘w’ tiene una substring sobre {a, b} cuyos alfabetos van de cero a infinito, pero el idioma a continuación no es aceptado por este DFA porque sus strings no siguen el formato de string.
L2 = {baa, aabaa, baabaaa..............}
El diagrama de transición de estado del idioma deseado será el siguiente: 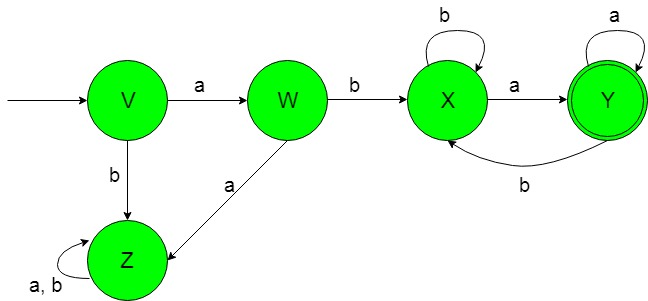
En el DFA anterior, el estado inicial ‘V’ al obtener ‘a’ como entrada, transita a un estado ‘W’ y al obtener ‘b’ como entrada transita a un estado muerto ‘Z’. El estado ‘W’ al obtener ‘a’ como entrada, transita al estado muerto ‘Z’ y al obtener ‘b’ como entrada, transita al estado ‘X’. El estado ‘X’ al tomar ‘b’ como entrada permanece en el estado de sí mismo y al tomar ‘a’ como entrada transita a un estado final ‘Y’.
El estado final ‘Y’ al obtener ‘a’ como entrada permanece en el estado de sí mismo y al obtener ‘b’ como entrada transita al estado ‘X’. El estado ‘Z’ se denomina estado muerto porque no puede ir al estado final nunca al obtener cualquiera de los alfabetos de entrada.
Problema-2: Construcción de un DFA mínimo que acepte un conjunto de strings sobre {a, b} en las que {a 2 bwa 2 / wε{a, b}*}.
Aquí ‘w’ es la substring que contiene alfabetos sobre cualquier número de ‘a’ y ‘b’ que van desde cero hasta el infinito.
Explicación: El idioma deseado será como:
L1 = {aabεaaa, aabaaaa, aababaaa, aabaabbaaa}
Aquí, como podemos ver, cada string del lenguaje anterior tiene una substring inicial constante, es decir, {a 2 b} y {a 2 } final, pero ‘w’ tiene una substring sobre {a, b} cuyos alfabetos van de cero a infinito pero Este DFA no acepta el siguiente idioma porque sus strings no siguen el formato de string.
L2 = {baa, abaa, baabaaa..............}
El diagrama de transición de estado del idioma deseado será el siguiente: 
En el DFA anterior, el estado inicial ‘A’ al obtener ‘a’ como entrada, transita a un estado ‘B’ y al obtener ‘b’ como entrada tránsito a un estado muerto ‘G’. El estado ‘B’ al obtener ‘a’ como entrada, transita a un estado ‘C’ y al obtener ‘b’ como entrada, transita a un estado muerto ‘G’. El estado ‘C’ al obtener ‘b’ como entrada, transita a un estado ‘D’ y al obtener ‘a’ como entrada, transita a un estado muerto ‘G’. El estado ‘D’ al obtener ‘a’ como entrada transita a un estado ‘E’ y al obtener ‘b’ como entrada permanece en el estado de sí mismo. El estado ‘E’ al obtener ‘a’ como entrada transita a un estado final ‘F’ y al obtener ‘b’ como entrada transita al estado ‘D’.
El estado final ‘F’ al obtener ‘a’ como entrada permanece en el estado de sí mismo y al obtener ‘b’ como entrada transita al estado ‘D’. El estado muerto ‘G’ se llama muerto porque no puede pasar al estado final al obtener cualquiera de los alfabetos de entrada.
Publicación traducida automáticamente
Artículo escrito por Kanchan_Ray y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA