Distribución t de Student en Estadística

La distribución t de Student o distribución t es una distribución de probabilidad que se utiliza para calcular los parámetros de la población cuando el tamaño de la muestra es pequeño y cuando se desconoce la varianza de la población. El trabajo teórico sobre la distribución t fue realizado por WS Gosset ; Ha publicado sus hallazgos bajo el seudónimo de “ Estudiante ”. Por eso se llama prueba t de Student . 

Es la distribución muestral del estadístico t. Los valores del estadístico t vienen dados por: 

t = [ x̄ - μ ] / [ s / sqrt( n ) ]

where,
t = t score
x̄ = sample mean,
μ = population mean,
s = standard deviation of the sample,
n = sample size 

¿Cuándo usar la distribución t? 

La distribución t de Student se utiliza cuando 

• El tamaño de la muestra debe ser de 30 o menos de 30.
• Se desconoce la desviación estándar de la población (σ).
• La distribución de la población debe ser unimodal y sesgada.

Derivación matemática de la distribución t: 

La distribución t se ha derivado matemáticamente bajo el supuesto de una población normalmente distribuida y la fórmula o ecuación será así 

f(t) = c(1+(t ² /ν)) ^{(-ν+1) / 2}

donde, 
c = Constante necesaria para que el área bajo la curva sea igual a la unidad 
ν = Grados de libertad 
 

Entonces, esta ecuación anterior indica la función de densidad de probabilidad (pdf) de la distribución t para ν grados de libertad. 

Propiedades de la Distribución t: 

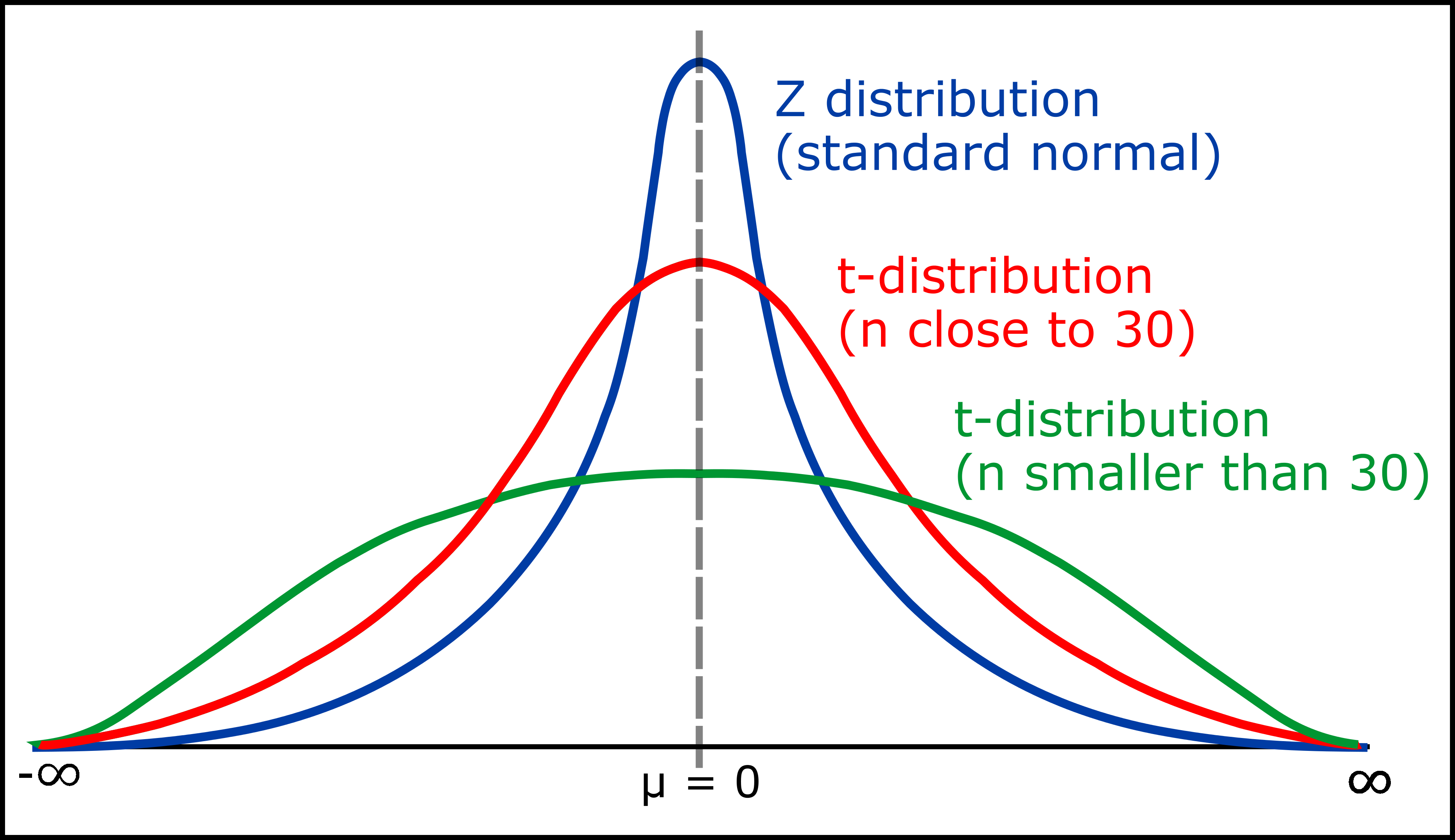
El diagrama anterior indica que la curva de color azul es una curva de distribución normal estándar o una curva de distribución Z porque el tamaño de la muestra (n) es mayor que 30. Y la curva de color rojo es una curva de distribución t porque el tamaño de la muestra (n) está cerca de 30. De manera similar, la curva de color verde también es una curva de distribución t porque el tamaño de la muestra (n) es menor que 30. 

La distribución t tiene las siguientes propiedades: 

• La variable en la distribución t varía de -∞ a +∞ ( -∞ < t < +∞ ).
• La distribución t será simétrica como la distribución normal, si el poder de t es par en la función de densidad de probabilidad (pdf).
• Para valores grandes de ν (es decir, tamaño de muestra aumentado n); la distribución t tiende a una distribución normal estándar. Esto implica que para diferentes valores de ν, la forma de la distribución t también difiere.
• La distribución t es menos puntiaguda que la distribución normal en el centro y más puntiaguda en las colas. En el diagrama anterior se puede observar que las curvas roja y verde tienen menos picos en el centro pero más picos en las colas que la curva azul.
• El valor de y (altura del pico) alcanza su punto más alto en μ = 0, ya que se puede observar lo mismo en el diagrama anterior.
• La media de la distribución es igual a 0 para ν > 1 donde ν = grados de libertad, de lo contrario indefinido.
• La mediana y la moda de la distribución es igual a 0.
• La varianza es igual a ν / ν-2 para ν > 2 y ∞ para 2 < ν ≤ 4 por lo demás indefinido.
• La asimetría es igual a 0 para ν > 3, de lo contrario no está definida.

Nota: 
los grados de libertad se refieren al número de observaciones independientes en un conjunto de datos. Al estimar una puntuación media o una proporción de una sola muestra, el número de observaciones independientes es igual al tamaño de la muestra menos uno. 
Por lo tanto, la distribución del estadístico t de muestras de tamaño 10 se describiría como una distribución que tiene 10 – 1 o 9 grados de libertad. De manera similar, se usaría una distribución t con 15 grados de libertad con una muestra de tamaño 16. 

Tabla de distribución 
t: la tabla de distribución t proporciona el valor t para un nivel diferente de significancia y diferentes grados de libertad. El valor t calculado se comparará con el valor t tabulado. Por ejemplo, si uno está realizando la prueba t de Student y para ese desempeño, ha tomado un nivel de significancia del 5% y obtuvo o calculó el valor t y tomó su valor t tabulado y si el valor t calculado es mayor que el valor t tabulado, en ese caso, dirá que hay una diferencia significativa entre la media de la población y las medias de la muestra al 5% de nivel de significación y si viceversa, entonces, en ese caso, dirá que no hay diferencia significativa entre la media de la población y las medias de la muestra al 5% de nivel de significación. Aquí está el enlace a la tabla de distribución t:http://www.ttable.org/