En una publicación anterior, Restoring Division aprendí sobre la restauración de la división. Ahora, aquí realice la división sin restauración, es menos compleja que la restauración porque se trata de una operación más simple, es decir, suma y resta, ahora también se realiza el paso de restauración. En el método, confíe en el bit de signo del registro que inicialmente contiene un cero denominado A.
Aquí está el diagrama de flujo que se muestra a continuación.
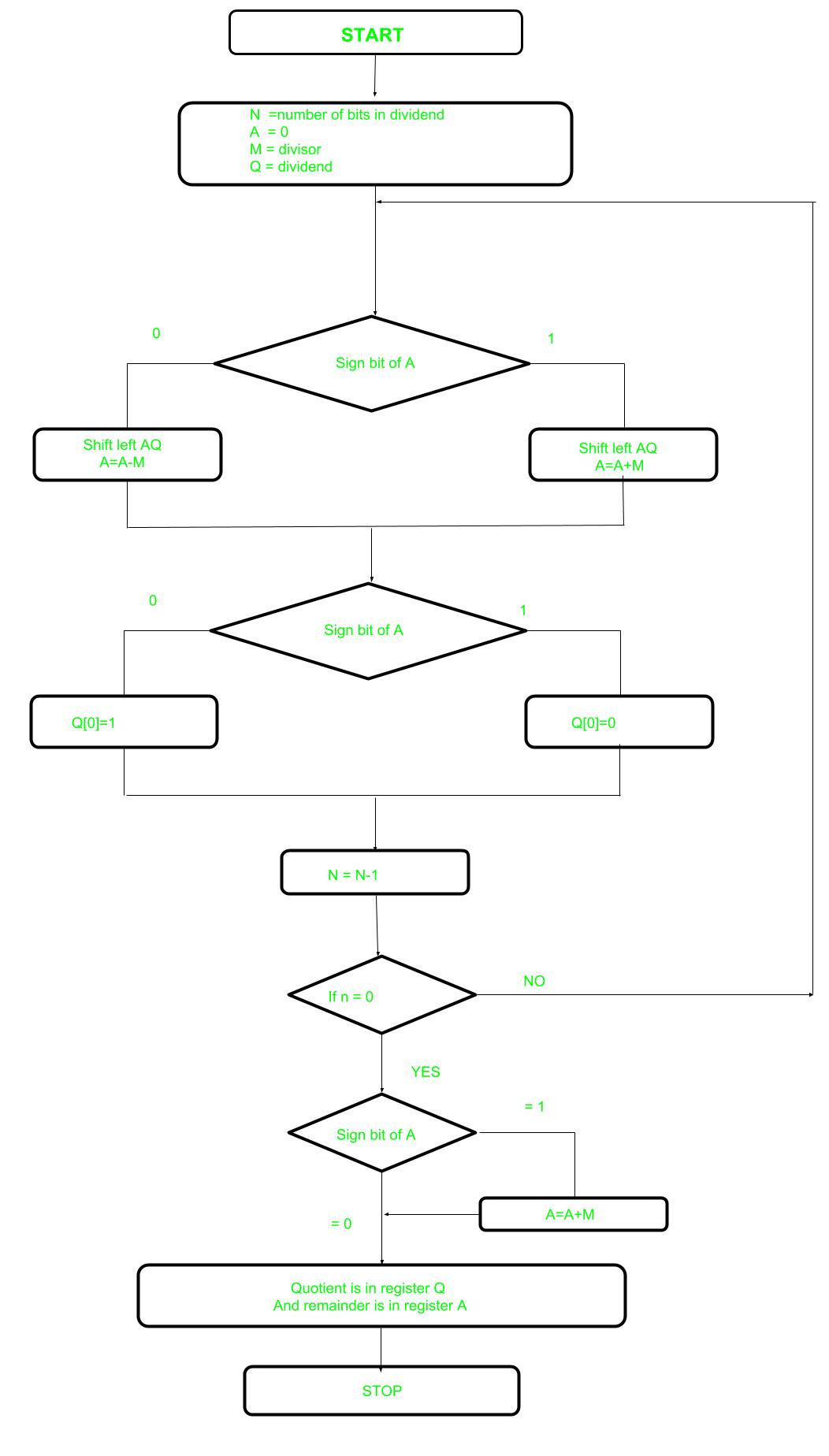
Escojamos el paso involucrado:
- Paso-1: Primero se inicializan los registros con los valores correspondientes (Q = Dividendo, M = Divisor, A = 0, n = número de bits en dividendo)
- Paso 2: verifique el bit de signo del registro A
- Paso 3: si es 1, cambie el contenido de AQ a la izquierda y realice A = A + M, de lo contrario, desplace AQ a la izquierda y realice A = AM (significa agregar el complemento de 2 de M a A y almacenarlo en A)
- Paso 4: Nuevamente el bit de signo del registro A
- Paso 5: si el bit de signo es 1, Q[0] se convierte en 0; de lo contrario, Q[0] se convierte en 1 (Q[0] significa el bit menos significativo del registro Q)
- Paso 6: Disminuye el valor de N en 1
- Paso 7: si N no es igual a cero, vaya al Paso 2 ; de lo contrario, vaya al siguiente paso
- Paso 8: si el bit de signo de A es 1, realice A = A+M
- Paso 9: el registro Q contiene cociente y A contiene resto
Ejemplos: realizar división sin restauración para enteros sin signo
Dividend =11 Divisor =3 -M =11101
| norte | METRO | A | q | Acción |
|---|---|---|---|---|
| 4 | 00011 | 00000 | 1011 | comienzo |
| 00001 | 011_ | Desplazamiento a la izquierda AQ | ||
| 11110 | 011_ | A=AM | ||
| 3 | 11110 | 0110 | Q[0]=0 | |
| 11100 | 110_ | Desplazamiento a la izquierda AQ | ||
| 11111 | 110_ | A=A+M | ||
| 2 | 11111 | 1100 | Q[0]=0 | |
| 11111 | 100_ | Desplazamiento a la izquierda AQ | ||
| 00010 | 100_ | A=A+M | ||
| 1 | 00010 | 1001 | Q[0]=1 | |
| 00101 | 001_ | Desplazamiento a la izquierda AQ | ||
| 00010 | 001_ | A=AM | ||
| 0 | 00010 | 0011 | Q[0]=1 |
Quotient = 3 (Q) Remainder = 2 (A)