Un termómetro con un bulbo lleno de líquido en un extremo, los líquidos más utilizados son el mercurio, el tolueno, el alcohol, el pentano y la creosota muestran lecturas diferentes para temperaturas distintas a la lectura fija debido a sus diferentes propiedades de expansión. Un termómetro que usa un gas, por otro lado, muestra la misma lectura de temperatura. No importa qué tipo de gas se utilice. Los experimentos muestran que todos los gases se expanden de la misma manera a bajas densidades.
Presión (P), volumen (V) y temperatura (T) donde T = t + 273.15 y t es la temperatura en °C son las variables que explican el comportamiento de una determinada cantidad (masa) de gas. La ley de los gases ideales, también conocida como ecuación universal de los gases, es un estado de ecuación para un gas ideal hipotético. A pesar de sus defectos, la ley de los gases ideales proporciona una buena aproximación del comportamiento de muchos gases en una variedad de situaciones. Benoit Paul Émile Clapeyron propuso la ley de los gases ideales en 1834 como una mezcla de la ley empírica de Charles, la ley de Boyle, la ley de Avogadro y la ley de Gay. de Lussac.
Ecuación de los gases ideales
Las leyes de los gases ideales son la combinación del trabajo de observación de Boyle en el siglo XVII y Charles en el siglo XVIII.
Ley de Boyle: La presión del gas es inversamente proporcional al volumen de gas para una cantidad dada de gas que se mantiene a una temperatura fija, es decir, a temperatura constante, la relación entre la presión y el volumen de una cantidad de gas se puede escribir como,
PAG ∝ 1 / V
o
VP = constante
donde P es la presión y V es el volumen.
Ley de Charles: el volumen del gas es directamente proporcional a la temperatura del gas para una cantidad fija dada de gas mantenida a una presión constante, es decir, a temperatura constante, la relación entre el volumen y la temperatura de una cantidad de gas se puede escribir como,
V ∝ T
o
V/T = Constante
donde T es la temperatura.
Estas dos leyes se aplican a los gases de baja densidad y se pueden agrupar en una sola relación. Vale la pena señalar que,
VP = constante
y
V/T = constante
Para una determinada cantidad de gas, entonces
Por lo tanto, PV/T también debería ser una constante.
Puede establecerse en una forma más general que se aplica a cualquier cantidad de cualquier gas de baja densidad, no simplemente a una cantidad específica de ese gas. Esta relación describe la ley de los gases ideales y se conoce como la ecuación de los gases ideales .
Se puede expresar como,
VP/T = nR
o
VP = nRT
donde, ni es el número de moles en la muestra de gas y R es la constante universal de los gases.
Nota: La constante universal de los gases (R) tiene un valor de 8,314 kJ/mol en el sistema SI.
También se puede establecer en una forma más general que se aplica a cualquier cantidad de cualquier gas de baja densidad, no simplemente a una cantidad específica de ese gas.
Derivación de la ecuación de los gases ideales
Sea P la presión ejercida por el gas, V el volumen del gas, T la temperatura.
Según la Ley de Boyle,
P ∝ 1/V
o
V ∝ 1/P ……(1)
Según la Ley de Charles,
V ∝ T ……..(2)
Según la Ley de Avogadro,
Cuando P y T son constantes, el volumen de un gas es proporcional al número de moles de gas.ie
V ∝ norte …….(3)
Compare la ecuación (1), (2) y (3) como,
V ∝ nT/P
o
VP = nRT
donde R es la constante universal de los gases y su valor es de 8.314 J/mol-K
Temperatura absoluta
La temperatura termodinámica es otro nombre para la temperatura absoluta . La energía termodinámica de un sistema es más baja a esta temperatura. La temperatura absoluta es igual a cero Kelvin o -273 °C, comúnmente conocido como cero absoluto . La velocidad de las partículas de gas se detiene en la temperatura cero absoluta. Esto significa que las partículas del gas realmente no se están moviendo. En el cero absoluto, el volumen del gas es cero. Como resultado, el volumen de un gas se mide por su cero absoluto.
La temperatura tiene una relación directa con la presión y el volumen, es decir
VA ∝ T
Esta relación permite obtener un gas que se utilizará para determinar la temperatura en un termómetro de gas con volumen constante.
Por lo tanto, a volumen constante, la relación se puede escribir como,
P ∝ T , y la temperatura se lee en términos de presión con un termómetro de gas de volumen constante.
Una línea recta emerge de una gráfica de presión contra temperatura.

A volumen constante, un gráfico de presión versus temperatura de un gas de baja densidad
Las observaciones sobre gases reales difieren de los valores previstos por la ley de los gases ideales a bajas temperaturas. Sin embargo, la relación es lineal en un amplio rango de temperatura y parece que si el gas siguiera siendo un gas, la presión caería a cero al disminuir la temperatura. Extrapolando la línea recta al eje se obtiene la temperatura mínima absoluta para un gas ideal. El cero absoluto se define como una temperatura de – 273,15 grados centígrados. La escala de temperatura Kelvin, a menudo conocida como temperatura de escala absoluta, se basa en el cero absoluto.
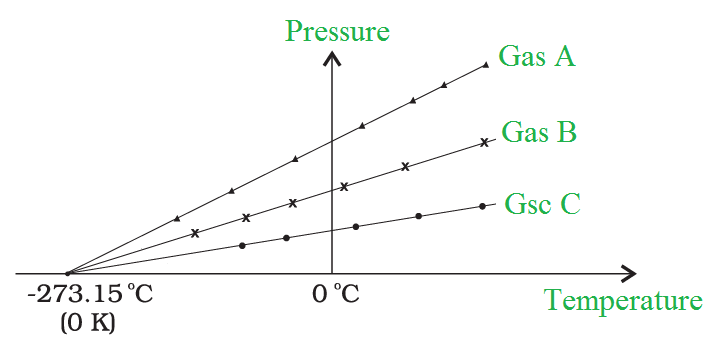
La misma temperatura del cero absoluto en un gráfico de presión versus temperatura y extrapolación de líneas para gases de baja densidad.
En la escala de temperatura Kelvin, – 273,15 °C se toma como punto cero, es decir, 0 K. Tanto en el sistema de temperatura Kelvin como en el Celsius, el tamaño de la unidad es el mismo. Entonces, la relación entre ellos se puede expresar como
t = t + 273,15
donde t es la temperatura en °C
Problemas de muestra
Problema 1: ¿Cuál es el volumen ocupado por 2,34 gramos de dirust de carbono gaseoso en STP?
Solución:
Dado,
El peso (m) del dirust de carbono es de 2,34 gramos.
En STP, la temperatura es de 273,0 K.
La presión es de 1,00 atm.
La constante universal de los gases (R) tiene un valor de 0,08206 L atm mol¯ 1 K¯ 1 .
La expresión para el número de moles es,
n = m/m
donde, n es el número de moles, m es el peso y M es la masa molar de la sustancia.
La masa molar del dirust de carbono es 44,0 g mol¯ 1 .
Entonces, el valor de n se puede calcular como,
n = 2,34 g / 44,0 g mol¯ 1
= 0,0532 moles
Según la ecuación de los gases ideales,
VP = nRT
Reordenando la ecuación,
V = nRT / P
Sustituyendo todos los valores,
V = [0,0532 mol) (0,08206 L atm mol¯1 K¯1) (273,0 K)] / 1,00 atm
= 1,19 litros
Problema 2: Una muestra de gas argón en STP ocupa 56,2 litros. Determine el número de moles de argón y la masa de argón en la muestra.
Solución:
Dado,
El volumen (V) del gas argón es de 56,2 litros.
En STP, la temperatura es de 273,0 K.
La presión es de 1,00 atm.
La masa molar del gas argón es 39,948 g/mol.
Según la ecuación de los gases ideales,
VP = nRT
Reordenando la ecuación,
n = PV / TR
Sustituyendo todos los valores en la ecuación anterior,
n = [(1,00 atm) (56,2 L) ] / [ (0,08206 L atm mol¯1 K¯1) (273,0 K)]
= 2,50866 moles
La expresión para el número de moles es
n = m/m
Reordenando la ecuación,
m = nM
Sustituyendo todos los valores en la ecuación anterior,
m = (2,50866 mol) × (39,948 g/mol)
= 100 gramos
Problema 3: ¿A qué temperatura 0,654 moles de gas neón ocuparán 12,30 litros a 1,95 atmósferas?
Solución:
Dado,
El Volumen (V) del gas neón es de 12,30 litros.
La presión es de 1,95 atm.
El número de moles es 0,654 moles.
Según la ecuación de los gases ideales,
VP = nRT
Reordenando la ecuación,
T = VP / nR
Sustituyendo todos los valores en la ecuación anterior,
T = [(1,95 atm) × (12,30 L)] / [(0,654 mol) × (0,08206 L atm mol¯ 1 K¯ 1 )]
= 447K
Problema 4: ¿Derivar la ecuación del gas ideal?
Solución:
Sea P la presión ejercida por el gas, V el volumen del gas, T la temperatura.
Según la Ley de Boyle,
P ∝ 1/V
o
V ∝ 1/P ……(1)
Según la Ley de Charles,
V ∝ T ……..(2)
Según la Ley de Avogadro,
Cuando P y T son constantes, el volumen de un gas es proporcional al número de moles de gas.ie
V ∝ norte …….(3)
Compare la ecuación (1), (2) y (3) como,
V ∝ nT/P
o
VP = nRT
donde R es la constante universal de los gases y su valor es de 8.314 J/mol-K
Problema 5: 5.600 g de CO2 sólido se colocan en un recipiente vacío sellado de 4.00 L a una temperatura de 300 K. Cuando todo el CO2 sólido se convierte en gas, ¿cuál será la presión en el recipiente?
Solución:
Dado,
El Peso (m) del dirust de carbono es de 5.600 g.
El Volumen (V) del dirust de carbono es 4.00 L.
La temperatura es de 300 K.
La masa molar del dirust de carbono es 44,0 g mol¯1
La expresión para el número de moles es
n = m/m
Sustituyendo todos los valores en la ecuación anterior,
n = (5,600 g) / (44,009 g/mol)
= 0,1272467 moles
Según la ecuación de los gases ideales,
VP = nRT
Reordenando la ecuación,
P = nRT/V
Sustituyendo todos los valores en la ecuación anterior,
P = (0,1272467 mol) × (0,08206 L atm mol¯ 1 K¯ 1 ) × (300 K)/ (4,00 L)
= 0,7831 atm
Publicación traducida automáticamente
Artículo escrito por anoopraj758 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA