Muchos de los movimientos que suceden a nuestro alrededor tienen una naturaleza circular. Desde un ventilador en el techo hasta una manecilla de reloj dando vueltas. Estos movimientos rodean cada aspecto de la vida diaria. Comprender el movimiento y predecir el movimiento de los cuerpos en tal movimiento. Es fundamental estudiar la dinámica del movimiento circular, esta dinámica incluye las ecuaciones de fuerza, aceleración y velocidad que gobiernan este movimiento. Veamos estos conceptos en detalle.
Movimiento circular
Se dice que un objeto que se mueve en una trayectoria circular alrededor de un punto realiza un movimiento circular. Por ejemplo, en términos generales, un vehículo que gira también es un ejemplo de un cuerpo que sigue un movimiento circular. El movimiento circular, si continúa, es de naturaleza periódica. Los movimientos periódicos son los movimientos que se repiten después de un cierto período de tiempo. Según la velocidad y la aceleración, este movimiento se puede clasificar en dos categorías:
- Movimiento Circular Uniforme: Cuando un cuerpo se mueve a velocidad constante en un movimiento circular a lo largo de la circunferencia de la trayectoria circular, se le llama Movimiento Circular Uniforme.
- Movimiento circular no uniforme: cuando un cuerpo se mueve en un movimiento circular a lo largo de la circunferencia de una trayectoria circular de tal manera que su velocidad sigue cambiando. Se llama movimiento circular no uniforme.
Dinámica del movimiento circular
Supongamos un movimiento circular en el que el cuerpo se mueve a una velocidad constante. Denotando el radio de la trayectoria circular en la que se mueve el cuerpo por “r”, y la velocidad del cuerpo por vm/s. La figura muestra el cuerpo yendo del punto A al punto B en el tiempo “t”. La longitud del arco desde el punto A hasta el punto B se denota por «s». En esto, el ángulo cubierto por el objeto está dado por,
θ = PQ/r
θ = s/r
La velocidad angular del cuerpo se define como la tasa de cambio del ángulo. Es similar a la velocidad en el caso del movimiento en línea recta. Se denota con el símbolo griego ω.
![]()
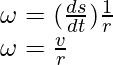
Fuerza centrípeta
En el caso de un movimiento circular uniforme, los cuerpos viajan con una velocidad constante. Por lo general, los cuerpos tienden a moverse en línea recta. Para que los cuerpos realicen un movimiento circular a una velocidad constante, debe haber alguna fuerza que los mantenga en una trayectoria circular. Tal fuerza se llama fuerza centrípeta. La reacción de esta fuerza se llama fuerza centrífuga. Esto significa que ambas fuerzas son iguales y de dirección opuesta.
La fuerza centrífuga está dada por,
![]()
Se sabe que, ω = v\r
Sustituyendo esta relación en la ecuación,
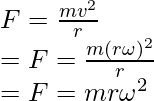
Problemas de muestra
Pregunta 1: Encuentra la velocidad angular de un cuerpo que se mueve a una velocidad de 50 m/s en un círculo de 5 m de radio.
Responder:
La fórmula para la velocidad angular está dada por,
Dado: v = 50 m/s y r = 5 m.
Reemplazando los valores en la ecuación,
ω = vr
⇒ ω = (50)(5)
⇒ ω = 250 rad/s
Pregunta 2: Encuentra la velocidad angular de un cuerpo que se mueve a una velocidad de 10 m/s en un círculo de 8 m de radio.
Responder:
La fórmula para la velocidad angular está dada por,
Dado: v = 10 m/s y r = 8 m.
Reemplazando los valores en la ecuación,
ω = vr
⇒ ω = (10)(8)
⇒ ω = 80 rad/s
Pregunta 3: Encuentra la fuerza que actúa sobre una partícula de 4 kg de masa que se mueve en un círculo de 4 m de radio a una velocidad de 5 m/s.
Responder:
La fórmula de la fuerza centrípeta está dada por,
Dado: v = 5 m/s, r = 4 m y m = 4Kg
Reemplazando los valores en la ecuación,
⇒
⇒ F = 25N
Pregunta 4: Encuentra la fuerza que actúa sobre una partícula de 8 kg de masa que se mueve en un círculo de 5 m de radio a una velocidad de 5 m/s.
Responder:
La fórmula de la fuerza centrípeta está dada por,
Dado: v = 5 m/s, r = 5m y m = 8Kg
Reemplazando los valores en la ecuación,
⇒
⇒ F = 40N
Pregunta 5: Encuentra la fuerza que actúa sobre una partícula de 10 kg de masa que se mueve en un círculo de 8 m de radio con una velocidad angular de 40 rad/s.
Responder:
La fórmula de la fuerza centrípeta está dada por,
F = mrω 2
Dado: ω = 40, r = 8 m y m = 10Kg
Reemplazando los valores en la ecuación,
F = mrω 2
⇒ F = (10)(8)(40) 2
⇒ F = (80)(1600)
⇒ F = 128000 N
Pregunta 6: Encuentra la fuerza que actúa sobre una partícula de 10 kg de masa que se mueve en un círculo de 8 m de radio con una velocidad angular de 40 rad/s.
Responder:
La fórmula de la fuerza centrípeta está dada por,
F = mrω 2
Dado: ω = 40, r = 8 m y m = 10Kg
Reemplazando los valores en la ecuación,
F = mrω 2
⇒ F = (10)(8)(40) 2
⇒ F = (80)(1600)
⇒ F = 128000 N
Pregunta 7: Un insecto se mueve en un círculo de 4 m de radio y completa 20 revoluciones por segundo. Encuentre la velocidad angular, la velocidad lineal y la aceleración.
Responder:
El cuerpo se mueve a 20 revoluciones por segundo.
ω = (Ángulo recorrido por segundo)
⇒ ω = (20 × 2π) = 40π
La velocidad angular es 40π rad/s.
La velocidad lineal viene dada por,
v = rω
Dado: r = 2 m
v = rω
⇒ v = (2)(40π)
⇒v = 80π
La aceleración estará dada por,
un =
⇒ un =
⇒ a = 3200π 2 rad/s 2
Pregunta 8: Un insecto se mueve en un círculo de 1 m de radio y completa 10 revoluciones por segundo. Encuentre la velocidad angular, la velocidad lineal y la aceleración.
Responder:
El cuerpo se mueve a 10 revoluciones por segundo.
ω = (Ángulo recorrido por segundo)
⇒ ω = (10 × 2π) = 20π
La velocidad angular es de 20π rad/s.
La velocidad lineal viene dada por,
v = rω
Dado: r = 1 m
v = rω
⇒ v = (1)(20π)
⇒v = 20π
La aceleración estará dada por,
un =
⇒ un =
⇒a = 200π 2 rad/s 2
Publicación traducida automáticamente
Artículo escrito por anjalishukla1859 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA
