El círculo más grande posible que se puede inscribir en un rectángulo.

Dado un rectángulo de largo l y ancho b , tenemos que encontrar el círculo más grande que se puede inscribir en el rectángulo. 
Ejemplos: 
 

Input  : l = 4, b = 8
Output : 12.56

Input  : l = 16 b = 6
Output : 28.26

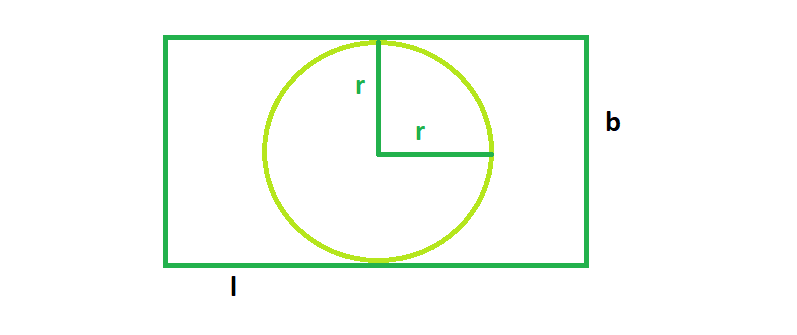
De la figura podemos ver que el círculo más grande que se puede inscribir en el rectángulo tendrá un radio siempre igual a la mitad del lado más corto del rectángulo. Así que de la figura,
 

radio, r = b/2 & 
Área, A = π * (r^2)

// C++ Program to find the biggest circle
// which can be inscribed  within the rectangle
#include <bits/stdc++.h>
using namespace std;
 
// Function to find the area
// of the biggest circle
float circlearea(float l, float b)
{
 
    // the length and breadth cannot be negative
    if (l < 0 || b < 0)
        return -1;
 
    // area of the circle
    if (l < b)
        return 3.14 * pow(l / 2, 2);
    else
        return 3.14 * pow(b / 2, 2);
}
 
// Driver code
int main()
{
    float l = 4, b = 8;
    cout << circlearea(l, b) << endl;
    return 0;
}

// Java Program to find the
// biggest circle which can be
// inscribed within the rectangle
 
class GFG
{
 
// Function to find the area
// of the biggest circle
static float circlearea(float l,
                        float b)
{
 
// the length and breadth
// cannot be negative
if (l < 0 || b < 0)
    return -1;
 
// area of the circle
if (l < b)
    return (float)(3.14 * Math.pow(l / 2, 2));
else
    return (float)(3.14 * Math.pow(b / 2, 2));
}
 
// Driver code
public static void main(String[] args)
{
    float l = 4, b = 8;
    System.out.println(circlearea(l, b));
}
}
 
// This code is contributed
// by ChitraNayal

# Python 3 Program to find the
# biggest circle which can be
# inscribed within the rectangle
 
# Function to find the area
# of the biggest circle
def circlearea(l, b):
 
    # the length and breadth
    # cannot be negative
    if (l < 0 or b < 0):
        return -1
 
    # area of the circle
    if (l < b):
        return 3.14 * pow(l // 2, 2)
    else:
        return 3.14 * pow(b // 2, 2)
 
# Driver code
if __name__ == "__main__":
    l = 4
    b = 8
    print(circlearea(l, b))
 
# This code is contributed
# by ChitraNayal

// C# Program to find the
// biggest circle which can be
// inscribed within the rectangle
using System;
 
class GFG
{
 
// Function to find the area
// of the biggest circle
static float circlearea(float l,
                        float b)
{
 
// the length and breadth
// cannot be negative
if (l < 0 || b < 0)
    return -1;
 
// area of the circle
if (l < b)
    return (float)(3.14 * Math.Pow(l / 2, 2));
else
    return (float)(3.14 * Math.Pow(b / 2, 2));
}
 
// Driver code
public static void Main()
{
    float l = 4, b = 8;
    Console.Write(circlearea(l, b));
}
}
 
// This code is contributed
// by ChitraNayal

<?php
// PHP Program to find the
// biggest circle which can be
// inscribed within the rectangle
 
// Function to find the area
// of the biggest circle
function circlearea($l, $b)
{
 
    // the length and breadth
    // cannot be negative
    if ($l < 0 || $b < 0)
        return -1;
 
    // area of the circle
    if ($l < $b)
        return 3.14 * pow($l / 2, 2);
    else
        return 3.14 * pow($b / 2, 2);
}
 
// Driver code
$l = 4;
$b = 8;
echo circlearea($l, $b)."\n";
 
// This code is contributed
// by ChitraNayal
?>

<script>
 
// javascript Program to find the
// biggest circle which can be
// inscribed within the rectangle
 
// Function to find the area
// of the biggest circle
function circlearea(l, b)
{
 
    // the length and breadth
    // cannot be negative
    if (l < 0 || b < 0)
        return -1;
     
    // area of the circle
    if (l < b)
        return (3.14 * Math.pow(l / 2, 2));
    else
        return (3.14 * Math.pow(b / 2, 2));
}
 
// Driver code
 
var l = 4, b = 8;
document.write(circlearea(l, b));
 
// This code is contributed by Amit Katiyar
 
</script>

12.56

Complejidad del tiempo: O(log l/2+log b/2)

Espacio Auxiliar: O(1)