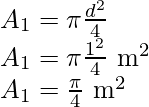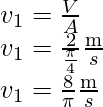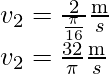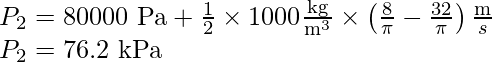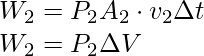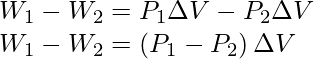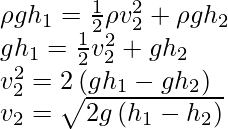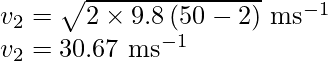El principio de Bernoulli

Los fluidos se pueden encontrar en todas partes a nuestro alrededor. La Tierra está rodeada de aire y el agua cubre dos tercios de su superficie. El agua no solo es vital para nuestra supervivencia; también es esencial para la supervivencia de todas las especies animales. Cada cuerpo de mamífero constituye principalmente agua. El fluido es diferente de un sólido, no tiene su propia forma distintiva. Un gas cubre toda la capacidad de su recipiente, mientras que los sólidos y los líquidos tienen un volumen fijo. El volumen se puede cambiar debido a cambios en la presión externa, es bastante pequeño en sólidos o líquidos, es decir, los sólidos y los líquidos son mucho menos comprimibles que los gases.

El esfuerzo cortante puede alterar la geometría de un sólido mientras mantiene su volumen. Los fluidos tienen una propiedad crítica: tienen muy poca resistencia al esfuerzo cortante; cuando se aplica una cantidad modesta de esfuerzo cortante, su forma cambia. Los fluidos tienen un esfuerzo cortante que es un millón de veces menor que los sólidos.

El principio de Bernoulli, introducido por Daniel Bernoulli , establece que a medida que aumenta la velocidad de un fluido (líquido o gas) que fluye, también aumenta la presión dentro del fluido. A pesar de que Bernoulli estableció la regla, fue Leonhard Euler quien desarrolló la ecuación de Bernoulli en su forma estándar en 1752.

El principio de Bernoulli establece que:

La energía mecánica neta del fluido que fluye, que incluye la energía potencial gravitacional de elevación, la energía de presión del fluido y la energía cinética del movimiento del fluido, permanece constante.

El flujo de fluidos es un concepto engañoso, sin embargo, la conservación de energía se usa para obtener algunas características útiles para flujos constantes o aerodinámicos. La expresión del principio de Bernoulli se originó utilizando el principio de conservación de la energía. Cuando esta teoría se aplica a fluidos en su estado ideal, tanto la densidad como la presión son inversamente proporcionales. Como resultado, un fluido que se mueve a un ritmo más lento ejercerá más fuerza que un fluido que se mueve a un ritmo más rápido.

Fórmula del principio de Bernoulli

La fórmula de la ecuación de Bernoulli es una relación entre la presión, la energía cinética y la energía potencial gravitacional de un fluido en un recipiente.

El principio de Bernoulli se define de la siguiente manera:

$P+\frac{1}{2}\rho v^2+\rho gh=\text{Constant}$

donde P es la presión ejercida, v es la velocidad, ρ es la densidad del fluido y h es la altura del recipiente.

Derivación de la ecuación de Bernoulli

Considere un fluido que corre a través de una tubería con un área de sección transversal variable y un fluido que no es compresible que corre a una velocidad constante. Como se ilustra en el diagrama, la tubería debe estar a varias alturas. Según la ecuación de continuidad, su velocidad debe fluctuar. Para lograr esto se requiere fuerza de aceleración, la cual es producida por el fluido que lo rodea, y la presión en diferentes lugares debe ser diferente.

La ecuación de Bernoulli es una formulación general que relaciona los cambios de velocidad, es decir, los cambios de energía cinética, y los cambios de altura, es decir, los cambios de energía potencial, con las diferencias de presión entre dos lugares de una tubería.

El flujo de un fluido ideal en una tubería de sección transversal variable.

Considere el flujo en dos regiones BC y DE. Observe el flujo en dos regiones diferentes: BC y DE. Considere que el fluido presente entre B y D viajaría en un intervalo de tiempo infinitesimal ∆t. Si v ₁ es la velocidad en B y v ₂ es la velocidad en D, el fluido en B ha viajado una distancia de v ₁ ∆t a C, es decir

dx ₁ = v ₁ Δt

En el mismo intervalo ∆t el fluido inicialmente en D se mueve a E, una distancia igual a v ₂ ∆t es decir

dx ₂ = v ₂ Δt

Las áreas A ₁ y A ₂ tienen las presiones P ₁ y P ₂ . El trabajo realizado sobre el fluido en BC es,

W ₁ = PAGS ₁ A ₁ ⋅ v ₁ Δt

= P ₁ ΔV

donde ∆V es el volumen que pasa por la región BC.

Dado que el mismo volumen ∆V pasa por las regiones BC y DE. por lo tanto, la expresión del trabajo realizado por el fluido en otro extremo DE es,

W ₂ = PAGS ₂ A ₂ ⋅ v ₂ Δt

= P2 _ΔV

Entonces el trabajo total realizado sobre el fluido es,

W ₁ – W ₂ = P ₁ ΔV – P ₂ ΔV

= ΔV (P ₁ – P ₂ )

Sea la densidad del fluido ρ por lo tanto la expresión:

∆m = ρ∆V es la masa que atraviesa la tubería en el tiempo ∆t. Entonces el cambio en la energía potencial gravitatoria es,

$\Delta{U} =\rho g\Delta{V}\left(h_{2}-h_{1}\right)$

El cambio en su energía cinética está dado por:

$\Delta{K}=\frac{1}{2}\rho\Delta{V}\left(v^2_{2}-v^2_{1}\right)$

Según el teorema del trabajo – energía’

$\left(P_{1}-P_{2}\right)\Delta{V}=\frac{1}{2}\rho \Delta{V}\left(v^2_{2}-v^2_{1}\right)+\rho g\Delta{V}\left(h_{2}-h_{1}\right)\\ \left(P_{1}-P_{2}\right)=\frac{1}{2}\rho\left(v^2_{2}-v^2_{1}\right)+\rho g\left(h_{2}-h_{1}\right)$

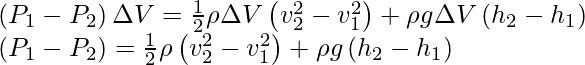
Reorganizar la expresión anterior,

$P_{1}+\frac{1}{2}\rho v^2_{1}+\rho gh_{1}=P_{2}+\frac{1}{2}\rho v^2_{2}+\rho gh_{2}$

Esta es la ecuación de Bernoulli y se puede escribir como una expresión general,

$P+\frac{1}{2}\rho v^2+\rho gh=\text{Constant}$

Aplicación del Principio de Bernoulli

Medidor Venturi: Un medidor Venturi es un dispositivo que mide la tasa de flujo de líquido a través de tuberías y se basa en el teorema de Bernoulli.
Avión: el teorema de Bernoulli rige el funcionamiento de los aviones. Las alas del avión tienen cierta forma. Cuando el avión se está moviendo, el aire pasa por él a gran velocidad, a pesar de la peluca de superficie baja del avión. Hay una variación en el flujo de aire por encima y por debajo de las alas debido al principio de Bernoulli. Como resultado del flujo de aire en la superficie superior del ala, este concepto provoca un cambio en la presión. Si la fuerza es mayor que la masa del avión, el avión ascenderá.
Efecto Magnus: una bola giratoria se aleja de su curso normal dentro del vuelo una vez que se lanza. El efecto Magnus es el nombre que recibe este fenómeno. Este impacto es importante en deportes como el cricket, el fútbol y el tenis.

Limitaciones del principio de Bernoulli

Las siguientes son las limitaciones del principio de Bernoulli:

Debido a la fricción, la velocidad de las partículas de fluido en el medio de un tubo disminuye gradualmente hacia la dirección del tubo. La velocidad de las partículas del líquido no es constante, por lo que se debe utilizar la velocidad media del líquido.
Esta ecuación de Bernoulli se puede utilizar para optimizar el suministro de líquido. Es ineficaz en flujo turbulento o irregular.
El flujo de líquido se verá afectado por la fuerza externa del líquido.
Este teorema se aplica preferentemente a fluidos sin viscosidad.
Se requiere fluido incompresible.
Cuando un fluido se desplaza en una trayectoria curva, se debe tener en cuenta la energía generada por las fuerzas centrífugas.
El flujo de líquido debe permanecer constante a lo largo del tiempo.
Una pequeña cantidad de energía cinética se puede convertir en energía térmica en un flujo inestable, y se puede perder algo de energía debido al esfuerzo cortante en un flujo espeso. Como resultado, estas pérdidas deben pasarse por alto.
El efecto de viscoso debe ser despreciable.

Problemas de muestra

Problema 1: El agua fluye a razón de 2m3s a través de un tubo con un diámetro de 1 m. Si la presión en este punto es de 80 kPa, ¿cuál es la presión del agua después de que el tubo se estrecha hasta un diámetro de 0,5 m? ρ _agua =1.0 kgl ^-1

Solución:

Según la expresión de Bernoulli:

$P_{1}+\frac{1}{2}\rho v^2_{1}+\rho gh_{1}=P_{2}+\frac{1}{2}\rho v^2_{2}+\rho gh_{2}$

La altura es la misma, por lo que la expresión se puede escribir como

$P_{2}=P_{1}+\frac{1}{2}\rho \left(v^2_{1}-v^2_{2}\right)$

La expresión para el área de la sección transversal es

$A_{1}=\pi\frac{ d^2}{4}\\ A_{1}=\pi\frac{ 1^2}{4}\text{ m}^2\\ A_{1}=\frac{\pi}{4}\text{ m}^2\\$

Similarmente

$A_{2}=\pi\frac{ d^2}{4}\\ A_{2}=\pi\frac{ 0.5^2}{4}\text{ m}^2\\ A_{2}=\frac{\pi}{16}\text{ m}^2\\$

La expresión de la velocidad para cada diámetro es

$v_1=\frac{V}{A}\\ v_1=\frac{2}{\frac{\pi}{4}}\frac{\text{m}}{s}\\ v_1=\frac{8}{\pi}\frac{\text{m}}{s}$

Similarmente,

$v_2=\frac{2}{\frac{\pi}{16}}\frac{\text{m}}{s}\\ v_2=\frac{32}{\pi}\frac{\text{m}}{s}$

Sustituye el valor en la expresión de Bernoulli:

$P_{2}=80000\text{ Pa}+\frac{1}{2}\times1000\frac{\text{kg}}{\text{m}^3}\times\left(\frac{8}{\pi}-\frac{32}{\pi}\right)\frac{\text{m}}{s}\\P_{2}=76.2\text{ kPa}$

Problema 2: Explique ¿por qué?

(a) La presión sanguínea en los humanos es mayor en los pies que en el cerebro.

(b) La presión atmosférica a una altura de unos 6 km disminuye a casi la mitad de su valor al nivel del mar, aunque la altura de la atmósfera es de más de 100 km.

(c) La presión hidrostática es una cantidad escalar aunque la presión sea la fuerza dividida por el área.

Solución:

(a) La altura de la columna de sangre en el pie es mayor que la del cerebro. Como resultado, la presión arterial humana es más alta en los pies que en el cerebro.

(b) La relación entre la densidad del aire y la altura no es lineal. Como resultado, la presión no disminuye linealmente con la altura. P = P ₀ e ^–αh da la presión del aire a una altura h, donde P ₀ es la presión del aire al nivel del mar y α es una constante.

(c) Cuando se aplica una fuerza a un líquido, la presión se distribuye uniformemente por todo el líquido. Como resultado, la presión debida al líquido no tiene una dirección definida. Como resultado, la presión hidrostática es un valor escalar.

Problema 3: Conduce la expresión del principio de Bernoulli.

Solución:

El flujo de un fluido ideal en una tubería de sección transversal variable. El fluido en una sección de longitud v ₁ ∆t se mueve a la sección de longitud v ₂ ∆t en el tiempo ∆t

Considere el flujo en dos regiones BC y DE. Observe el flujo en dos regiones diferentes: BC y DE. Considere que el fluido presente entre B y D viajaría en un intervalo de tiempo infinitesimal ∆t. Si v ₁ es la velocidad en B y v ₂ es la velocidad en D, el fluido en B ha viajado una distancia de v ₁ ∆t a C, es decir

$dx_{1}=v_{1}\Delta{t}$

En el mismo intervalo ∆t el fluido inicialmente en D se mueve a E, una distancia igual a v2∆t es decir

$dx_{2}=v_{2}\Delta{t}$

Las áreas A ₁ y A ₂ tienen las presiones P ₁ y P ₂ . El trabajo realizado sobre el fluido en BC es

$W_{1}=P_{1}A_{1}\cdot v_{1}\Delta{t}\\ W_{1}=P_{1}\Delta{V}$

donde ∆V es el volumen que pasa por la región BC.

Dado que el mismo volumen ∆V pasa por las regiones BC y DE. por lo tanto, la expresión del trabajo realizado por el fluido en el otro extremo DE es

$W_{2}=P_{2}A_{2}\cdot v_{2}\Delta{t}\\ W_{2}=P_{2}\Delta{V}$

Entonces el trabajo total realizado sobre el fluido es $P+\frac{1}{2}\rho v^2+\rho gv^2=contant$

$W_{1}-W_{2}=P_{1}\Delta{V}-P_{2}\Delta{V}\\ W_{1}-W_{2}=\left(P_{1}-P_{2}\right)\Delta{V}$

Deje que la densidad del fluido sea ρ, por lo tanto, la expresión ∆m = ρ∆V es la masa que pasa a través de la tubería en el tiempo ∆t, luego el cambio en la energía potencial gravitatoria es

$\Delta{U} =\rho g\Delta{V}\left(h_{2}-h_{1}\right)$

El cambio en su energía cinética está dado por

$\Delta{K}=\frac{1}{2}\rho\Delta{V}\left(v^2_{2}-v^2_{1}\right)$

Según el trabajo – teorema de la energía

$\left(P_{1}-P_{2}\right)\Delta{V}=\frac{1}{2}\rho \Delta{V}\left(v^2_{2}-v^2_{1}\right)+\rho g\Delta{V}\left(h_{2}-h_{1}\right)\\ \left(P_{1}-P_{2}\right)=\frac{1}{2}\rho\left(v^2_{2}-v^2_{1}\right)+\rho g\left(h_{2}-h_{1}\right)$

Reorganizar la expresión anterior,

$P_{1}+\frac{1}{2}\rho v^2_{1}+\rho gh_{1}=P_{2}+\frac{1}{2}\rho v^2_{2}+\rho gh_{2}$

Esta es la ecuación de Bernoulli y se puede escribir como expresión general.

Esta es la ecuación de Bernoulli y se puede escribir como expresión general,

$P+\frac{1}{2}\rho v^2+\rho gh=contant$

Problema 4: Cuáles son las limitaciones del principio de Bernoulli.

Solución:

Las siguientes son las limitaciones del principio de Bernoulli:

Debido a la fricción, la velocidad de las partículas de fluido en el medio de un tubo disminuye gradualmente hacia la dirección del tubo. la velocidad de las partículas del líquido no es constante, por lo que se debe utilizar la velocidad media del líquido.

Esta ecuación de Bernoulli se puede utilizar para optimizar el suministro de líquido. Es ineficaz en flujo turbulento o irregular.

El flujo de líquido se verá afectado por la fuerza externa del líquido.

Este teorema se aplica preferentemente a fluidos sin viscosidad.

Se requiere fluido incompresible.

Cuando un fluido se desplaza en una trayectoria curva, se debe tener en cuenta la energía generada por las fuerzas centrífugas.

El flujo de líquido debe permanecer constante a lo largo del tiempo.

Una pequeña cantidad de energía cinética se puede convertir en energía térmica en un flujo inestable, y se puede perder algo de energía debido al esfuerzo cortante en un flujo espeso. Como resultado, estas pérdidas deben pasarse por alto.

El efecto de viscoso debe ser despreciable.

Problema 5: Supongamos que un enorme tanque de 50 m de altura y lleno de agua está abierto a la atmósfera y es alcanzado por una bala que perfora un lado del tanque, permitiendo que el agua fluya hacia afuera. El agujero está a 2 m sobre el suelo. Si el agujero es muy pequeño en comparación con el tamaño del tanque, ¿con qué rapidez saldrá el agua del tanque?

Solución:

Según la expresión de Bernoulli:

$P_{1}+\frac{1}{2}\rho v^2_{1}+\rho gh_{1}=P_{2}+\frac{1}{2}\rho v^2_{2}+\rho gh_{2}$

Según la pregunta, se supone que la parte superior del recipiente es el punto 1 y el orificio por donde sale el agua es el punto 2. Ambos puntos están abiertos a la atmósfera. Por lo tanto, la presión en cada lado de la ecuación anterior es igual a 1 atm y, por lo tanto, se canceló. El tamaño del agujero en el costado del tanque es tan pequeño en comparación con el resto del tanque que la velocidad del agua en el punto 1 es casi igual a 0. Por lo tanto, podemos cancelar el $\frac{1}{2}ρv^2_1$ término en el lado izquierdo del tanque. ecuación. La expresión puede reescribirse como,

$\rho gh_1=\frac{1}{2}\rho v^2_{2}+\rho gh_{2}\\ gh_1=\frac{1}{2}v^2_{2}+gh_{2}\\v^2_{2}=2\left(gh_1-gh_2\right)\\v_{2}=\sqrt{2g\left(h_1-h_2\right)}\\$

Sustituya los valores en la expresión anterior,

$v_{2}=\sqrt{2\times9.8\left(50-2\right)}\text{ ms}^{-1}\\v_{2}=30.67\text{ ms}^{-1}$

Publicación traducida automáticamente

Artículo escrito por anoopraj758 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA