El problema del intervalo de existencias

Posted on by Rudeus Greyrat

El problema de la duración de las acciones es un problema financiero en el que tenemos una serie de n cotizaciones diarias de precios para una acción y necesitamos calcular la duración del precio de las acciones para todos los n días. El lapso Si del precio de la acción en un día dado i se define como el número máximo de días consecutivos justo antes del día dado, para los cuales el precio de la acción en el día actual es menor que su precio en el día dado. 
Ejemplo:

Entrada: N = 7, precio[] = [100 80 60 70 60 75 85]
Salida: 1 1 1 2 1 4 6
Explicación: Recorrer el intervalo de entrada dado para 100 será 1, 80 es menor que 100, por lo que el intervalo es 1, 60 es menor que 80, por lo que el intervalo es 1, 70 es mayor que 60, por lo que el intervalo es 2 y así sucesivamente. Por lo tanto, la salida será 1 1 1 2 1 4 6.

Entrada: N = 6, precio[] = [10 4 5 90 120 80]
Salida: 1 1 2 4 5 1
Explicación: Recorrer el intervalo de entrada dado para 10 será 1, 4 es menor que 10, por lo que el intervalo será 1 , 5 es mayor que 4 por lo que el lapso será 2 y así sucesivamente. Por lo tanto, la salida será 1 1 2 4 5 1.

 

Un método simple pero ineficiente 
Atraviesa la array de precios de entrada. Para cada elemento que se visite, recorra los elementos a la izquierda e incremente el valor de amplitud del mismo mientras que los elementos del lado izquierdo son más pequeños.

A continuación se muestra la implementación de este método:

C++

// C++ program for brute force method 
// to calculate stock span values 
#include <bits/stdc++.h>
using namespace std; 
  
// Fills array S[] with span values 
void calculateSpan(int price[], int n, int S[]) 
{ 
    // Span value of first day is always 1 
    S[0] = 1; 
  
    // Calculate span value of remaining days  
    // by linearly checking previous days 
    for (int i = 1; i < n; i++) 
    { 
        S[i] = 1; // Initialize span value 
  
        // Traverse left while the next element  
        // on left is smaller than price[i] 
        for (int j = i - 1; (j >= 0) && 
                (price[i] >= price[j]); j--) 
            S[i]++; 
    } 
} 
  
// A utility function to print elements of array 
void printArray(int arr[], int n) 
{ 
    for (int i = 0; i < n; i++) 
        cout << arr[i] << " "; 
} 
  
// Driver code 
int main() 
{ 
    int price[] = { 10, 4, 5, 90, 120, 80 }; 
    int n = sizeof(price) / sizeof(price[0]); 
    int S[n]; 
  
    // Fill the span values in array S[] 
    calculateSpan(price, n, S); 
  
    // print the calculated span values 
    printArray(S, n); 
  
    return 0; 
} 
  
// This is code is contributed by rathbhupendra

C

// C program for brute force method to calculate stock span values
#include <stdio.h>
  
// Fills array S[] with span values
void calculateSpan(int price[], int n, int S[])
{
    // Span value of first day is always 1
    S[0] = 1;
  
    // Calculate span value of remaining days by linearly checking
    // previous days
    for (int i = 1; i < n; i++) {
        S[i] = 1; // Initialize span value
  
        // Traverse left while the next element on left is smaller
        // than price[i]
        for (int j = i - 1; (j >= 0) && (price[i] >= price[j]); j--)
            S[i]++;
    }
}
  
// A utility function to print elements of array
void printArray(int arr[], int n)
{
    for (int i = 0; i < n; i++)
        printf("%d ", arr[i]);
}
  
// Driver program to test above function
int main()
{
    int price[] = { 10, 4, 5, 90, 120, 80 };
    int n = sizeof(price) / sizeof(price[0]);
    int S[n];
  
    // Fill the span values in array S[]
    calculateSpan(price, n, S);
  
    // print the calculated span values
    printArray(S, n);
  
    return 0;
}

Java

// Java implementation for brute force method to calculate stock span values
  
import java.util.Arrays;
  
class GFG {
    // method to calculate stock span values
    static void calculateSpan(int price[], int n, int S[])
    {
        // Span value of first day is always 1
        S[0] = 1;
  
        // Calculate span value of remaining days by linearly checking
        // previous days
        for (int i = 1; i < n; i++) {
            S[i] = 1; // Initialize span value
  
            // Traverse left while the next element on left is smaller
            // than price[i]
            for (int j = i - 1; (j >= 0) && (price[i] >= price[j]); j--)
                S[i]++;
        }
    }
  
    // A utility function to print elements of array
    static void printArray(int arr[])
    {
        System.out.print(Arrays.toString(arr));
    }
  
    // Driver program to test above functions
    public static void main(String[] args)
    {
        int price[] = { 10, 4, 5, 90, 120, 80 };
        int n = price.length;
        int S[] = new int[n];
  
        // Fill the span values in array S[]
        calculateSpan(price, n, S);
  
        // print the calculated span values
        printArray(S);
    }
}
// This code is contributed by Sumit Ghosh

Python3

# Python program for brute force method to calculate stock span values
  
# Fills list S[] with span values
def calculateSpan(price, n, S):
      
    # Span value of first day is always 1
    S[0] = 1
  
    # Calculate span value of remaining days by linearly 
    # checking previous days
    for i in range(1, n, 1):
        S[i] = 1   # Initialize span value
  
        # Traverse left while the next element on left is
        # smaller than price[i]
        j = i - 1
        while (j>= 0) and (price[i] >= price[j]) :
                       S[i] += 1
                       j -= 1
                         
# A utility function to print elements of array
def printArray(arr, n):
  
    for i in range(n):
        print(arr[i], end = " ")
  
# Driver program to test above function    
price = [10, 4, 5, 90, 120, 80]
n = len(price)
S = [None] * n
  
# Fill the span values in list S[]
calculateSpan(price, n, S)
  
# print the calculated span values
printArray(S, n)
  
  
# This code is contributed by Sunny Karira

C#

// C# implementation for brute force method
// to calculate stock span values
using System;
  
class GFG {
  
    // method to calculate stock span values
    static void calculateSpan(int[] price,
                              int n, int[] S)
    {
  
        // Span value of first day is always 1
        S[0] = 1;
  
        // Calculate span value of remaining
        // days by linearly checking previous
        // days
        for (int i = 1; i < n; i++) {
            S[i] = 1; // Initialize span value
  
            // Traverse left while the next
            // element on left is smaller
            // than price[i]
            for (int j = i - 1; (j >= 0) && (price[i] >= price[j]); j--)
                S[i]++;
        }
    }
  
    // A utility function to print elements
    // of array
    static void printArray(int[] arr)
    {
        string result = string.Join(" ", arr);
        Console.WriteLine(result);
    }
  
    // Driver function
    public static void Main()
    {
        int[] price = { 10, 4, 5, 90, 120, 80 };
        int n = price.Length;
        int[] S = new int[n];
  
        // Fill the span values in array S[]
        calculateSpan(price, n, S);
  
        // print the calculated span values
        printArray(S);
    }
}
  
// This code is contributed by Sam007.

PHP

<?php
// PHP program for brute force method
// to calculate stock span values
  
// Fills array S[] with span values
function calculateSpan($price, $n, $S)
{
      
    // Span value of first
    // day is always 1
    $S[0] = 1;
      
    // Calculate span value of 
    // remaining days by linearly 
    // checking previous days
    for ($i = 1; $i < $n; $i++)
    {
          
        // Initialize span value
        $S[$i] = 1; 
      
        // Traverse left while the next
        // element on left is smaller
        // than price[i]
        for ($j = $i - 1; ($j >= 0) && 
            ($price[$i] >= $price[$j]); $j--)
            $S[$i]++;
    }
      
        // print the calculated 
        // span values
        for ($i = 0; $i < $n; $i++)
        echo $S[$i] . " ";;
      
          
}
  
    // Driver Code
    $price = array(10, 4, 5, 90, 120, 80);
    $n = count($price);
    $S = array($n);
  
    // Fill the span values in array S[]
    calculateSpan($price, $n, $S);
  
// This code is contributed by Sam007
?>

JavaScript

<script>
    // Javascript implementation for brute force method
    // to calculate stock span values
      
    // method to calculate stock span values
    function calculateSpan(price, n, S)
    {
   
        // Span value of first day is always 1
        S[0] = 1;
   
        // Calculate span value of remaining
        // days by linearly checking previous
        // days
        for (let i = 1; i < n; i++) {
            S[i] = 1; // Initialize span value
   
            // Traverse left while the next
            // element on left is smaller
            // than price[i]
            for (let j = i - 1; (j >= 0) && (price[i] >= price[j]); j--)
                S[i]++;
        }
    }
   
    // A utility function to print elements
    // of array
    function printArray(arr)
    {
        let result = arr.join(" ");
        document.write(result);
    }
      
    let price = [ 10, 4, 5, 90, 120, 80 ];
    let n = price.length;
    let S = new Array(n);
    S.fill(0);
  
    // Fill the span values in array S[]
    calculateSpan(price, n, S);
  
    // print the calculated span values
    printArray(S);
  
</script>
Producción

1 1 2 4 5 1

La Complejidad de Tiempo del método anterior es O(n^2). Podemos calcular los valores de stock span en tiempo O(n).

Un método de complejidad de tiempo lineal 
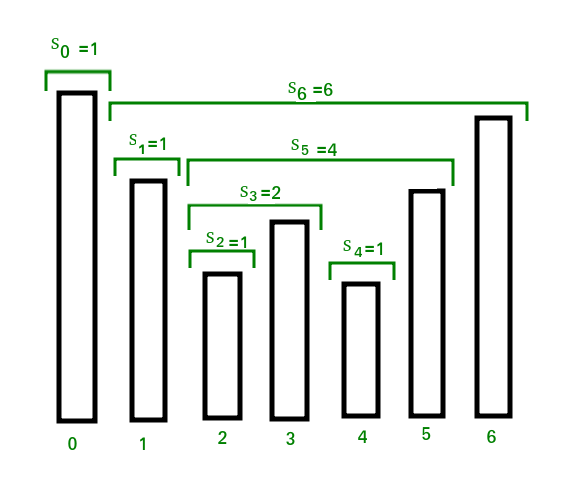
Vemos que S[i] en el día i se puede calcular fácilmente si conocemos el día más cercano que precede a i , de modo que el precio es mayor que ese día que el precio del día i. Si tal día existe, llamémoslo h(i) , de lo contrario, definimos h(i) = -1 . 
El intervalo ahora se calcula como S[i] = i – h(i) . Vea el siguiente diagrama.
 

Para implementar esta lógica, usamos una pila como tipo de datos abstractos para almacenar los días i, h(i), h(h(i)), etc. Cuando pasamos del día i-1 al i, extraemos los días en que el precio de la acción fue menor o igual que el precio[i] y luego empujamos el valor del día i de vuelta a la pila.
A continuación se muestra la implementación de este método. 

También debemos verificar si el precio de todas las acciones debe ser el mismo, por lo tanto, solo debemos verificar si el precio actual de las acciones es mayor que el anterior o no. No saldremos de la pila cuando los precios de las acciones actuales y anteriores sean los mismos. 

C++

// C++ linear time solution for stock span problem
#include <iostream>
#include <stack>
using namespace std;
  
// A stack based efficient method to calculate
// stock span values
void calculateSpan(int price[], int n, int S[])
{
    // Create a stack and push index of first
    // element to it
    stack<int> st;
    st.push(0);
  
    // Span value of first element is always 1
    S[0] = 1;
  
    // Calculate span values for rest of the elements
    for (int i = 1; i < n; i++) {
        // Pop elements from stack while stack is not
        // empty and top of stack is smaller than
        // price[i]
        while (!st.empty() && price[st.top()] <= price[i])
            st.pop();
  
        // If stack becomes empty, then price[i] is
        // greater than all elements on left of it,
        // i.e., price[0], price[1], ..price[i-1].  Else
        // price[i] is greater than elements after
        // top of stack
        S[i] = (st.empty()) ? (i + 1) : (i - st.top());
  
        // Push this element to stack
        st.push(i);
    }
}
  
// A utility function to print elements of array
void printArray(int arr[], int n)
{
    for (int i = 0; i < n; i++)
        cout << arr[i] << " ";
}
  
// Driver program to test above function
int main()
{
    int price[] = { 10, 4, 5, 90, 120, 80 };
    int n = sizeof(price) / sizeof(price[0]);
    int S[n];
  
    // Fill the span values in array S[]
    calculateSpan(price, n, S);
  
    // print the calculated span values
    printArray(S, n);
  
    return 0;
}

Java

// Java linear time solution for stock span problem
  
import java.util.ArrayDeque;
import java.util.Deque;
import java.util.Arrays;
  
  
public class GFG {
    // A stack based efficient method to calculate
    // stock span values
    static void calculateSpan(int price[], int n, int S[])
    {
        // Create a stack and push index of first element
        // to it
        Deque<Integer> st = new ArrayDeque<Integer>();
        //Stack<Integer> st = new Stack<>();
        st.push(0);
  
        // Span value of first element is always 1
        S[0] = 1;
  
        // Calculate span values for rest of the elements
        for (int i = 1; i < n; i++) {
  
            // Pop elements from stack while stack is not
            // empty and top of stack is smaller than
            // price[i]
            while (!st.isEmpty() && price[st.peek()] <= price[i])
                st.pop();
  
            // If stack becomes empty, then price[i] is
            // greater than all elements on left of it, i.e.,
            // price[0], price[1], ..price[i-1]. Else price[i]
            // is greater than elements after top of stack
            S[i] = (st.isEmpty()) ? (i + 1) : (i - st.peek());
  
            // Push this element to stack
            st.push(i);
        }
    }
  
    // A utility function to print elements of array
    static void printArray(int arr[])
    {
        System.out.print(Arrays.toString(arr));
    }
  
    // Driver method
    public static void main(String[] args)
    {
        int price[] = { 10, 4, 5, 90, 120, 80 };
        int n = price.length;
        int S[] = new int[n];
  
        // Fill the span values in array S[]
        calculateSpan(price, n, S);
  
        // print the calculated span values
        printArray(S);
    }
}
// This code is contributed by Sumit Ghosh

Python3

# Python linear time solution for stock span problem
  
# A stack based efficient method to calculate s
def calculateSpan(price, S):
      
    n = len(price)
    # Create a stack and push index of first element to it
    st = [] 
    st.append(0)
  
    # Span value of first element is always 1
    S[0] = 1
  
    # Calculate span values for rest of the elements
    for i in range(1, n):
          
        # Pop elements from stack while stack is not
        # empty and top of stack is smaller than price[i]
        while( len(st) > 0 and price[st[-1]] <= price[i]):
            st.pop()
  
        # If stack becomes empty, then price[i] is greater
        # than all elements on left of it, i.e. price[0],
        # price[1], ..price[i-1]. Else the price[i] is
        # greater than elements after top of stack
        S[i] = i + 1 if len(st) <= 0 else (i - st[-1])
  
        # Push this element to stack
        st.append(i)
  
  
# A utility function to print elements of array
def printArray(arr, n):
    for i in range(0, n):
        print (arr[i], end =" ")
  
  
# Driver program to test above function
price = [10, 4, 5, 90, 120, 80]
S = [0 for i in range(len(price)+1)]
  
# Fill the span values in array S[]
calculateSpan(price, S)
  
# Print the calculated span values
printArray(S, len(price))
  
# This code is contributed by Nikhil Kumar Singh (nickzuck_007)

C#

// C# linear time solution for
// stock span problem
using System;
using System.Collections;
  
class GFG {
    // a linear time solution for
    // stock span problem A stack
    // based efficient method to calculate
    // stock span values
    static void calculateSpan(int[] price, int n, int[] S)
    {
        // Create a stack and Push
        // index of first element to it
        Stack st = new Stack();
        st.Push(0);
  
        // Span value of first
        // element is always 1
        S[0] = 1;
  
        // Calculate span values
        // for rest of the elements
        for (int i = 1; i < n; i++) {
  
            // Pop elements from stack
            // while stack is not empty
            // and top of stack is smaller
            // than price[i]
            while (st.Count > 0 && price[(int)st.Peek()] <= price[i])
                st.Pop();
  
            // If stack becomes empty, then price[i] is
            // greater than all elements on left of it, i.e.,
            // price[0], price[1], ..price[i-1]. Else price[i]
            // is greater than elements after top of stack
            S[i] = (st.Count == 0) ? (i + 1) : (i - (int)st.Peek());
  
            // Push this element to stack
            st.Push(i);
        }
    }
  
    // A utility function to print elements of array
    static void printArray(int[] arr)
    {
        for (int i = 0; i < arr.Length; i++)
            Console.Write(arr[i] + " ");
    }
  
    // Driver method
    public static void Main(String[] args)
    {
        int[] price = { 10, 4, 5, 90, 120, 80 };
        int n = price.Length;
        int[] S = new int[n];
  
        // Fill the span values in array S[]
        calculateSpan(price, n, S);
  
        // print the calculated span values
        printArray(S);
    }
}
  
// This code is contributed by Arnab Kundu

JavaScript

<script>
// javascript linear time solution for stock span problem
  
    // A stack based efficient method to calculate
    // stock span values
    function calculateSpan(price , n , S)
    {
      
        // Create a stack and push index of first element
        // to it
        var st = [];
        st.push(0);
  
        // Span value of first element is always 1
        S[0] = 1;
  
        // Calculate span values for rest of the elements
        for (var i = 1; i < n; i++) {
  
            // Pop elements from stack while stack is not
            // empty and top of stack is smaller than
            // price[i]
            while (st.length!==0 && price[st[st.length - 1]] <= price[i])
                st.pop();
  
            // If stack becomes empty, then price[i] is
            // greater than all elements on left of it, i.e.,
            // price[0], price[1], ..price[i-1]. Else price[i]
            // is greater than elements after top of stack
            S[i] = (st.length===0) ? (i + 1) : (i - st[st.length - 1]);
  
            // Push this element to stack
            st.push(i);
        }
    }
  
    // A utility function to print elements of array
    function printArray(arr) {
        document.write(arr);
    }
  
    // Driver method
      
        var price = [ 10, 4, 5, 90, 120, 80 ];
        var n = price.length;
        var S = Array(n).fill(0);
  
        // Fill the span values in array S
        calculateSpan(price, n, S);
  
        // print the calculated span values
        printArray(S);
  
// This code contributed by Rajput-Ji
</script>
Producción

1 1 2 4 5 1

Complejidad temporal : O(n). Parece más que O(n) a primera vista. Si observamos más de cerca, podemos observar que cada elemento de la array se agrega y elimina de la pila como máximo una vez. Así que hay un total de 2n operaciones como máximo. Suponiendo que una operación de pila requiere un tiempo O(1), podemos decir que la complejidad del tiempo es O(n).
Espacio auxiliar : O(n) en el peor de los casos cuando todos los elementos se ordenan en orden decreciente.

Otro enfoque: (sin usar la pila)  

C++

// C++ program for a linear time solution for stock
// span problem without using stack
#include <iostream>
#include <stack>
using namespace std;
  
// An efficient method to calculate stock span values
// implementing the same idea without using stack
void calculateSpan(int A[], int n, int ans[])
{
    // Span value of first element is always 1
    ans[0] = 1;
  
    // Calculate span values for rest of the elements
    for (int i = 1; i < n; i++) {
        int counter = 1;
        while ((i - counter) >= 0 && A[i] >= A[i - counter]) {
            counter += ans[i - counter];
        }
        ans[i] = counter;
    }
}
  
// A utility function to print elements of array
void printArray(int arr[], int n)
{
    for (int i = 0; i < n; i++)
        cout << arr[i] << " ";
}
  
// Driver program to test above function
int main()
{
    int price[] = { 10, 4, 5, 90, 120, 80 };
    int n = sizeof(price) / sizeof(price[0]);
    int S[n];
  
    // Fill the span values in array S[]
    calculateSpan(price, n, S);
  
    // print the calculated span values
    printArray(S, n);
  
    return 0;
}

Java

// Java program for a linear time
// solution for stock span problem
// without using stack
class GFG {
  
    // An efficient method to calculate
    // stock span values implementing the
    // same idea without using stack
    static void calculateSpan(int A[],
                              int n, int ans[])
    {
        // Span value of first element is always 1
        ans[0] = 1;
  
        // Calculate span values for rest of the elements
        for (int i = 1; i < n; i++) {
            int counter = 1;
            while ((i - counter) >= 0 && A[i] >= A[i - counter]) {
                counter += ans[i - counter];
            }
            ans[i] = counter;
        }
    }
  
    // A utility function to print elements of array
    static void printArray(int arr[], int n)
    {
        for (int i = 0; i < n; i++)
            System.out.print(arr[i] + " ");
    }
  
    // Driver code
    public static void main(String[] args)
    {
        int price[] = { 10, 4, 5, 90, 120, 80 };
        int n = price.length;
        int S[] = new int[n];
  
        // Fill the span values in array S[]
        calculateSpan(price, n, S);
  
        // print the calculated span values
        printArray(S, n);
    }
}
  
/* This code contributed by PrinciRaj1992 */

Python3

# Python3 program for a linear time
# solution for stock span problem 
# without using stack 
  
# An efficient method to calculate 
# stock span values implementing 
# the same idea without using stack 
def calculateSpan(A, n, ans):
      
    # Span value of first element
    # is always 1 
    ans[0] = 1
  
    # Calculate span values for rest
    # of the elements 
    for i in range(1, n):
        counter = 1
          
        while ((i - counter) >= 0 and 
              A[i] >= A[i - counter]):
            counter += ans[i - counter]
        ans[i] = counter
  
# A utility function to print elements
# of array 
def printArray(arr, n):
      
    for i in range(n):
        print(arr[i], end = ' ')
    print()
  
# Driver code
price = [ 10, 4, 5, 90, 120, 80 ]
n = len(price)
S = [0] * (n)
  
# Fill the span values in array S[] 
calculateSpan(price, n, S) 
  
# Print the calculated span values 
printArray(S, n)
  
# This code is contributed by Prateek Gupta 

C#

// C# program for a linear time
// solution for stock span problem
// without using stack
using System;
public class GFG {
  
    // An efficient method to calculate
    // stock span values implementing the
    // same idea without using stack
    static void calculateSpan(int[] A,
                              int n, int[] ans)
    {
        // Span value of first element is always 1
        ans[0] = 1;
  
        // Calculate span values for rest of the elements
        for (int i = 1; i < n; i++) {
            int counter = 1;
            while ((i - counter) >= 0 && A[i] >= A[i - counter]) {
                counter += ans[i - counter];
            }
            ans[i] = counter;
        }
    }
  
    // A utility function to print elements of array
    static void printArray(int[] arr, int n)
    {
        for (int i = 0; i < n; i++)
            Console.Write(arr[i] + " ");
    }
  
    // Driver code
    public static void Main(String[] args)
    {
        int[] price = { 10, 4, 5, 90, 120, 80 };
        int n = price.Length;
        int[] S = new int[n];
  
        // Fill the span values in array S[]
        calculateSpan(price, n, S);
  
        // print the calculated span values
        printArray(S, n);
    }
}
// This code has been contributed by 29AjayKumar

JavaScript

<script>
 
       // JavaScript program for the above approach;
 
       // An efficient method to calculate stock span values
       // implementing the same idea without using stack
       function calculateSpan(A, n, ans)
       {
         
           // Span value of first element is always 1
           ans[0] = 1;
 
           // Calculate span values for rest of the elements
           for (let i = 1; i < n; i++) {
               let counter = 1;
               while ((i - counter) >= 0 && A[i] >= A[i - counter]) {
                   counter += ans[i - counter];
               }
               ans[i] = counter;
           }
       }
 
       // A utility function to print elements of array
       function printArray(arr, n) {
           for (let i = 0; i < n; i++)
               document.write(arr[i] + " ");
       }
 
       // Driver program to test above function
       let price = [10, 4, 5, 90, 120, 80];
       let n = price.length;
       let S = new Array(n);
 
       // Fill the span values in array S[]
       calculateSpan(price, n, S);
 
       // print the calculated span values
       printArray(S, n);
         
  // This code is contributed by Potta Lokesh
   </script>
Producción

1 1 2 4 5 1

Un enfoque basado en la pila:

  1. En este enfoque, he usado la pila de estructura de datos para implementar esta tarea.
  2. Aquí, se utilizan dos pilas. Una pila almacena los precios reales de las acciones, mientras que la otra pila es una pila temporal.
  3. El problema de stock span se resuelve usando solo las funciones Push y Pop de Stack.
  4. Solo para tomar valores de entrada, tomé la array ‘precio’ y para almacenar la salida, usé la array ‘intervalo’.

A continuación se muestra la implementación del enfoque anterior:

C

// C program for the above approach
#include <limits.h>
#include <stdio.h>
#include <stdlib.h>
#define SIZE 6
  
// change size of  stack from here
// change this char to int if 
// you want to create stack of
// int. rest all program will work fine
typedef int stackentry;
  
typedef struct stack {
    stackentry entry[SIZE];
    int top;
} STACK;
  
// stack is initialized by setting top pointer = -1.
void initialiseStack(STACK* s) { s->top = -1; }
  
// to check if stack is full.
int IsStackfull(STACK s)
{
    if (s.top == SIZE - 1) {
        return (1);
    }
    return (0);
}
  
// to check if stack is empty.
int IsStackempty(STACK s)
{
    if (s.top == -1) {
        return (1);
    }
    else {
        return (0);
    }
}
  
// to push elements into the stack.
void push(stackentry d, STACK* s)
{
    if (!IsStackfull(*s)) {
  
        s->entry[(s->top) + 1] = d;
        s->top = s->top + 1;
    }
}
  
// to pop element from stack.
stackentry pop(STACK* s)
{
    stackentry ans;
    if (!IsStackempty(*s)) {
        ans = s->entry[s->top];
        s->top = s->top - 1;
    }
    else {
        
        // '\0'  will be returned if 
        // stack is empty and of
        // char type.
        if (sizeof(stackentry) == 1)
            ans = '\0';
        else
            // INT_MIN  will be returned 
            // if stack is empty
            // and of int type.
            ans = INT_MIN;
    }
    return (ans);
}
  
// The code for implementing stock 
// span problem is written
// here in main function.
int main()
{
    // Just to store prices on 7 adjacent days
    int price[6] = { 10, 4, 5, 90, 120, 80 };
    
    // in span array , span of each day will be stored.
    int span[6] = { 0 };
    int i;
    
    // stack 's' will store stock values of each
    // day. stack 'temp' is temporary stack
    STACK s, temp; 
    
    // setting top pointer to -1.
    initialiseStack(&s); 
    initialiseStack(&temp);
    
    // count basically signifies span of
    // particular day.
    int count = 1; 
    
    // since first day span is 1 only.
    span[0] = 1; 
    push(price[0], &s);
    
    // calculate span of remaining days.
    for (i = 1; i < 6; i++) {
        
        // count will be span of that particular day.
        count = 1;
        
        // if current day stock is larger than previous day
        // span, then it will be popped out into temp stack.
        // popping will be carried out till span gets over
        // and count will be incremented .
  
        while (!IsStackempty(s)
               && s.entry[s.top] <= price[i]) {
            push(pop(&s), &temp);
            count++;
        } 
          
        // now, one by one all stocks from temp will be
        // popped and pushed back to s.
        while (!IsStackempty(temp)) {
            push(pop(&temp), &s);
        }
        
        // pushing current stock
        push(price[i], &s);
        
        // appending span of that particular
        // day into output array.
        span[i] = count; 
    }
    
    // printing the output.
    for (i = 0; i < 6; i++)
        printf("%d ", span[i]);
}

C++

// C++ program for brute force method 
// to calculate stock span values 
#include <bits/stdc++.h>
using namespace std; 
  
  
vector <int> calculateSpan(int arr[], int n)
    {
       // Your code here
        stack<int> s;
        vector<int> ans;
        for(int i=0;i<n;i++)
        {
            while(!s.empty() and arr[s.top()] <= arr[i])
                        s.pop();
                      
            if(s.empty())
                ans.push_back(i+1);
            else
            {
                int top = s.top();
                    ans.push_back(i-top);
            }
            s.push(i);
        }
      
        return ans;
    }
      
// A utility function to print elements of array 
void printArray(vector<int> arr) 
{ 
    for (int i = 0; i < arr.size(); i++) 
        cout << arr[i] << " "; 
} 
  
// Driver code 
int main() 
{ 
    int price[] = { 10, 4, 5, 90, 120, 80 }; 
    int n = sizeof(price) / sizeof(price[0]); 
    int S[n]; 
  
      
    vector<int> arr = calculateSpan(price, n); 
    printArray(arr);
     
  
    return 0; 
} 
  
// This is code is contributed by Arpit Jain

Java

// Java program for brute force method
// to calculate stock span values
  
import java.util.ArrayList;
import java.util.ArrayDeque;
import java.util.Deque;
  
class GFG {
  
    static ArrayList<Integer> calculateSpan(int arr[],
                                            int n)
    {
        // Your code here
        Deque<Integer> s = new ArrayDeque<Integer>();
        ArrayList<Integer> ans = new ArrayList<Integer>();
        for (int i = 0; i < n; i++) {
            while (!s.isEmpty() && arr[s.peek()] <= arr[i])
                s.pop();
  
            if (s.isEmpty())
                ans.add(i + 1);
            else {
                int top = s.peek();
                ans.add(i - top);
            }
            s.push(i);
        }
  
        return ans;
    }
  
    // A utility function to print elements of array
    static void printArray(ArrayList<Integer> arr)
    {
        for (int i = 0; i < arr.size(); i++)
            System.out.print(arr.get(i) + " ");
    }
  
    // Driver code
    public static void main(String args[])
    {
        int price[] = { 10, 4, 5, 90, 120, 80 };
        int n = price.length;
  
        ArrayList<Integer> arr = calculateSpan(price, n);
        printArray(arr);
    }
}
  
// This is code is contributed by Lovely Jain

Python3

# Python3 program for a linear time
# solution for stock span problem 
# using stack 
def calculateSpan(a, n):
    s = []      
    ans = []
    for i in range(0,n):
          
        while(s != [] and a[s[-1]] <= a[i]):
            s.pop()
          
        if(s == []):
            ans.append(i+1)
          
        else:
            top = s[-1]
            ans.append(i - top)
          
        s.append(i)
      
    return ans
  
# A utility function to print elements
# of array 
def printArray(arr, n):
      
    for i in range(n):
        print(arr[i], end = ' ')
    print()
  
# Driver code
price = [ 10, 4, 5, 90, 120, 80 ]
n = len(price)
ans = calculateSpan(price, n) 
  
# Print the calculated span values 
printArray(ans, n)
  
# This code is contributed by Arpit Jain
Producción

1 1 2 4 5 1

que era el mismo resultado esperado.

Complejidad de tiempo: O(N) , donde N es el tamaño de la array. 
Complejidad espacial: O(N) , donde N es el tamaño de la array. 

Publicación traducida automáticamente

Artículo escrito por GeeksforGeeks-1 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Deja una respuesta

Tu dirección de correo electrónico no será publicada. Los campos obligatorios están marcados con *