Eliminación de ruido usando el filtro Butterworth digital de paso bajo en Scipy – Python

En este artículo, la tarea es escribir un programa de Python para la eliminación de ruido utilizando el filtro Butterworth digital de paso bajo.

¿Qué es el ruido?

El ruido es básicamente la parte no deseada de una señal electrónica. A menudo se genera debido a fallas en el diseño, conexiones sueltas, fallas en los interruptores, etc.

¿Qué hacer si tenemos ruido en nuestra señal?

Para eliminar señales/ruidos no deseados, utilizamos filtros de diferentes tipos y especificaciones. En general, en la industria, necesitamos elegir el mejor ajuste probándolo con la señal para identificar el mejor filtro que se utilizará para eliminar el ruido en un caso de uso determinado.

¿Qué vamos a hacer ahora?

Vamos a implementar un filtro Butterworth digital de paso bajo ahora para eliminar la señal/ruido no deseado de una combinación de ondas sinusoidales.

Especificaciones del filtro:

• Señal compuesta por 25 Hz y 50 Hz
• Frecuencia de muestreo 1kHz.
• Ordene N=10 a 35Hz para eliminar el tono de 50Hz.

Paso a paso:

Paso 1: Importación de las bibliotecas

# import required library
import numpy as np
import scipy.signal as signal
import matplotlib.pyplot as plt

Paso 2: Definición de las especificaciones

# Specifications of the filter
f1 = 25  # Frequency of 1st signal
f2 = 50  # Frequency of 2nd signal
N = 10  # Order of the filter
  
  
# Generate the time vector of 1 sec duration
t = np.linspace(0, 1, 1000)  # Generate 1000 samples in 1 sec
  
# Generate the signal containing f1 and f2
sig = np.sin(2*np.pi*f1*t) + np.sin(2*np.pi*f2*t)

Paso 3: Trace la señal original con ruido

# Display the signal
fig, (ax1, ax2) = plt.subplots(2, 1, sharex=True)
ax1.plot(t, sig)
ax1.set_title('25 Hz and 50 Hz sinusoids')
ax1.axis([0, 1, -2, 2])
  
# Design the Butterworth filter using 
# signal.butter and output='sos'
sos = signal.butter(50, 35, 'lp', fs=1000, output='sos')

Producción:

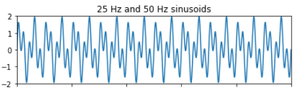
Paso 4: Gráfico de la señal después de eliminar el ruido 

# Filter the signal by the filter using signal.sosfilt
# Use signal.sosfiltfilt to get output inphase with input
filtered = signal.sosfiltfilt(sos, sig)
  
  
# Display the output signal
ax2.plot(t, filtered)
ax2.set_title('After 35 Hz Low-pass filter')
ax2.axis([0, 1, -2, 2])
ax2.set_xlabel('Time [seconds]')
plt.tight_layout()
plt.show()

Producción:

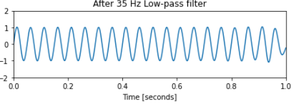
Paso 5: Implementación

# import required library
import numpy as np
import scipy.signal as signal
import matplotlib.pyplot as plt
  
# Given
f1 = 25  # Frequency of 1st signal
f2 = 50  # Frequency of 2nd signal
N = 10  # Order of the filter
  
# Generate the time vector of 1 sec duration
# START CODE HERE ### (≈ 1 line of code)
# Generate 1000 samples in 1 sec
t = np.linspace(0, 1, 1000)
  
# Generate the signal containing f1 and f2
# START CODE HERE ### (≈ 1 line of code)
sig = np.sin(2*np.pi*f1*t) + np.sin(2*np.pi*f2*t)
  
# Display the signal
fig, (ax1, ax2) = plt.subplots(2, 1, sharex=True)
ax1.plot(t, sig)
ax1.set_title('25 Hz and 50 Hz sinusoids')
ax1.axis([0, 1, -2, 2])
  
# Design the Butterworth filter using signal.butter and output='sos'
# START CODE HERE ### (≈ 1 line of code)
sos = signal.butter(50, 35, 'lp', fs=1000, output='sos')
  
# Filter the signal by the filter using signal.sosfilt
# START CODE HERE ### (≈ 1 line of code)
# Use signal.sosfiltfilt to get output inphase with input
filtered = signal.sosfiltfilt(sos, sig)
  
  
# Display the output signal
ax2.plot(t, filtered)
ax2.set_title('After 35 Hz Low-pass filter')
ax2.axis([0, 1, -2, 2])
ax2.set_xlabel('Time [seconds]')
plt.tight_layout()
plt.show()

Producción: