Dado un árbol binario y un Node K, la tarea es eliminar el Node K asegurándose de que el árbol se reduzca desde la parte inferior (es decir, el Node eliminado se reemplaza por el Node más inferior y más a la derecha) usando Level Order Traversal .
Ejemplos:
Entrada: K = 8, Árbol =
Producción:
Explicación:
Consulte a continuación para obtener una explicación.Entrada: K = 1, Árbol =
Producción:
Acercarse:
- Comience a buscar desde la raíz, la dirección del Node que se eliminará atravesando en orden de nivel .
- Continúe atravesando el árbol para encontrar el Node más profundo y más a la derecha en orden de nivel para encontrar el Node más profundo y más a la derecha.
- Si el Node a eliminar es diferente del Node más profundo a la derecha, reemplace el Node que se eliminará con el Node más profundo a la derecha y elimine el Node posterior
- Si el Node a eliminar es el mismo que el Node más profundo a la derecha, simplemente elimine el Node.
Por ejemplo: Considere el Ejemplo 1 de arriba
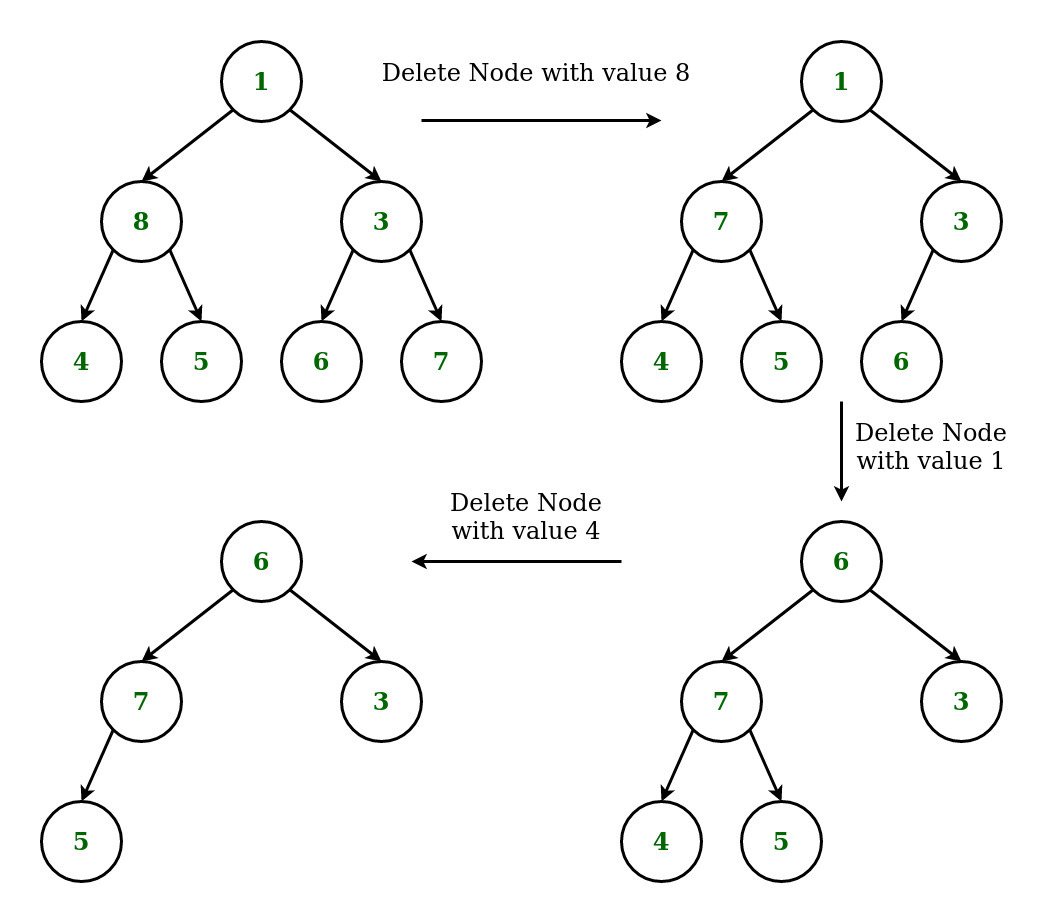
A continuación se muestra la implementación del enfoque anterior.
C++
// C++ implementation to delete a node
// in Binary Tree using Level Order Traversal
#include <bits/stdc++.h>
using namespace std;
// Structure of Binary Tree
struct node {
int data;
node* left;
node* right;
};
// Function to create new node
// of a Binary Tree.
node* newnode(int d)
{
node* temp = new node;
temp->data = d;
temp->left = temp->right = NULL;
return temp;
}
// Function for Level Order
// Traversal of Binary Tree
void levelorder(node* curr)
{
// Queue to store the nodes
// in a level
queue<node*> q;
if (curr)
q.push(curr);
// Loop to Traverse the Binary
// Tree in Level Order
while (!q.empty()) {
curr = q.front();
q.pop();
cout << curr->data << " ";
if (curr->left)
q.push(curr->left);
if (curr->right)
q.push(curr->right);
}
}
// Function to Delete the deepest
// right-most node of the Binary Tree
void deletedeepest(node* root,
node* temp)
{
queue<node*> q;
q.push(root);
// Loop to Traverse Binary Tree
// in level order and delete Node
while (!q.empty()) {
node* T = q.front();
q.pop();
if (T->right == temp) {
T->right = NULL;
delete (temp);
return;
}
else
q.push(T->right);
if (T->left == temp) {
T->left = NULL;
delete (temp);
return;
}
else
q.push(T->left);
}
}
// Function to Delete Node
// in Binary Tree
node* deletenode(node* root, int data)
{
if (root == NULL)
return NULL;
// Condition if the Root node
// is a leaf node.
if (root->left == NULL
&& root->right == NULL) {
if (root->data == data) {
return NULL;
}
else
return root;
}
queue<node*> q;
q.push(root);
node* temp = NULL;
node* nodetodelete = NULL;
// Loop to Traverse Tree in
// Level Order and find the
// Rightmost Deepest Node of the
// Binary Tree and Node to be Deleted
while (!q.empty()) {
temp = q.front();
q.pop();
if (temp->data == data) {
nodetodelete = temp;
}
if (temp->left) {
q.push(temp->left);
}
if (temp->right) {
q.push(temp->right);
}
}
// if node to be deleted is not found
if (nodetodelete != NULL) {
// Condition to check if node to delete
// is not same as node to replace
if (temp != nodetodelete) {
int t = temp->data;
deletedeepest(root, temp);
nodetodelete->data = t;
}
// if node to delete is also
// rightmost deepest node
else {
deletedeepest(root, temp);
}
}
return root;
}
// Driver Code
int main()
{
// Construction of Tree
node* root = newnode(1);
root->left = newnode(8);
root->right = newnode(3);
root->left->left = newnode(4);
root->left->right = newnode(5);
root->right->left = newnode(6);
root->right->right = newnode(7);
cout << "Original Tree: ";
levelorder(root);
// Deleting node with key 8
root = deletenode(root, 8);
cout << endl;
cout << "Deleting node with key 8: ";
levelorder(root);
// Deleting node with key 1
root = deletenode(root, 1);
cout << endl;
cout << "Deleting node with key 1: ";
levelorder(root);
// Deleting node with key 4
root = deletenode(root, 4);
cout << endl;
cout << "Deleting node with key 4: ";
levelorder(root);
}
Java
// Java implementation to delete a node
// in Binary Tree using Level Order Traversal
import java.util.LinkedList;
import java.util.Queue;
// Binary Tree
class TreeNode
{
int data;
TreeNode left = null;
TreeNode right = null;
TreeNode(int data)
{
this.data = data;
}
}
class BinaryTreeDeleteKNode{
public TreeNode insert(TreeNode root,
int value)
{
if (root == null)
{
root = new TreeNode(value);
return root;
}
// Do level order traversal and add
// node to first null
Queue<TreeNode> q = new LinkedList<TreeNode>();
q.add(root);
while (!q.isEmpty())
{
TreeNode tn = q.remove();
if (tn.left != null)
{
q.add(tn.left);
}
else
{
tn.left = new TreeNode(value);
return root;
}
if (tn.right != null)
{
q.add(tn.right);
}
else
{
tn.right = new TreeNode(value);
return root;
}
}
return root;
}
// Function for Level Order
// Traversal of Binary Tree
public void levelOrder(TreeNode root)
{
if (root == null)
{
System.out.println("Tree is empty!!");
}
// Queue to store the nodes
// in a level
Queue<TreeNode> q = new LinkedList<TreeNode>();
q.add(root);
// Loop to Traverse the Binary
// Tree in Level Order
while (!q.isEmpty())
{
TreeNode tn = q.remove();
System.out.print(tn.data + " ");
if (tn.left != null)
q.add(tn.left);
if (tn.right != null)
q.add(tn.right);
}
}
// Function to delete node node with value K
public TreeNode deleteIn(TreeNode root, int k)
{
if (root == null)
return root;
// Do level order traversal if node found
// with the value k then select that node
// keep traversal till we find deepest
// node with empty value keep track of
// the parent node of the deepest node
TreeNode searchedNode = null;
TreeNode tn = null;
Queue<TreeNode> q = new LinkedList<TreeNode>();
TreeNode deepestNodeParent = null;
q.add(root);
while (!q.isEmpty())
{
boolean isParent = false;
tn = q.remove();
if (searchedNode == null && tn.data == k)
{
searchedNode = tn;
}
if (tn.left != null)
{
q.add(tn.left);
isParent = true;
}
if (tn.right != null)
{
q.add(tn.right);
isParent = true;
}
if (isParent) deepestNodeParent = tn;
}
if (searchedNode == null)
{
System.out.print("Node with value '" + k +
"' not exists.");
return root;
}
searchedNode.data = tn.data;
if (deepestNodeParent != null &&
deepestNodeParent.left != null &&
deepestNodeParent.left.data == tn.data)
{
deepestNodeParent.left = null;
}
else
{
deepestNodeParent.right = null;
}
return root;
}
// Driver code
public static void main(String[] args)
{
TreeNode node = null;
BinaryTreeDeleteKNode binaryTreeDeleteKNode = new BinaryTreeDeleteKNode();
// Construction of Tree
node = binaryTreeDeleteKNode.insert(node, 1);
node = binaryTreeDeleteKNode.insert(node, 8);
node = binaryTreeDeleteKNode.insert(node, 3);
node = binaryTreeDeleteKNode.insert(node, 4);
node = binaryTreeDeleteKNode.insert(node, 5);
node = binaryTreeDeleteKNode.insert(node, 6);
node = binaryTreeDeleteKNode.insert(node, 7);
System.out.print("Original Tree: ");
binaryTreeDeleteKNode.levelOrder(node);
// Deleting node with key 8
node = binaryTreeDeleteKNode.deleteIn(node,8);
System.out.print("\nDeleting node with key 8: ");
binaryTreeDeleteKNode.levelOrder(node);
// Deleting node with key 1
node = binaryTreeDeleteKNode.deleteIn(node,1);
System.out.print("\nDeleting node with key 1: ");
binaryTreeDeleteKNode.levelOrder(node);
// Deleting node with key 4
node = binaryTreeDeleteKNode.deleteIn(node,4);
System.out.print("\nDeleting node with key 4: ");
binaryTreeDeleteKNode.levelOrder(node);
}
}
// This code is contributed by anshulgtbit91
Python3
# Python3 implementation to delete a node
# in Binary Tree using Level Order Traversal
from collections import deque
# Structure of Binary Tree
class Node:
def __init__(self, x):
self.data = x
self.left = None
self.right = None
# Function for Level Order
# Traversal of Binary Tree
def levelorder(curr):
# Queue to store the nodes
# in a level
q = deque()
if (curr):
q.append(curr)
# Loop to Traverse the Binary
# Tree in Level Order
while len(q) > 0:
curr = q.popleft()
#q.pop()
print(curr.data, end = " ")
if (curr.left):
q.append(curr.left)
if (curr.right):
q.append(curr.right)
# Function to Delete the deepest
# right-most node of the Binary Tree
def deletedeepest(root, temp):
q = deque()
q.append(root)
# Loop to Traverse Binary Tree
# in level order and delete Node
while (len(q) > 0):
T = q.popleft()
#q.pop()
if (T.right == temp):
T.right = None
#delete (temp)
return
else:
q.append(T.right)
if (T.left == temp):
T.left = None
#delete (temp)
return
else:
q.append(T.left)
# Function to Delete Node
# in Binary Tree
def deletenode(root, data):
if (root == None):
return None
# Condition if the Root node
# is a leaf node.
if (root.left == None and
root.right == None):
if (root.data == data):
return None
else:
return root
q = deque()
q.append(root)
temp = None
nodetodelete = None
# Loop to Traverse Tree in
# Level Order and find the
# Rightmost Deepest Node of the
# Binary Tree and Node to be Deleted
while (len(q) > 0):
temp = q.popleft()
#q.pop()
if (temp.data == data):
nodetodelete = temp
if (temp.left):
q.append(temp.left)
if (temp.right):
q.append(temp.right)
# If node to be deleted is not found
if (nodetodelete != None):
# Condition to check if node to delete
# is not same as node to replace
if (temp != nodetodelete):
t = temp.data
deletedeepest(root, temp)
nodetodelete.data = t
# If node to delete is also
# rightmost deepest node
else:
deletedeepest(root, temp)
return root
# Driver Code
if __name__ == '__main__':
# Construction of Tree
root = Node(1)
root.left = Node(8)
root.right = Node(3)
root.left.left = Node(4)
root.left.right = Node(5)
root.right.left = Node(6)
root.right.right = Node(7)
print("Original Tree: ", end = "")
levelorder(root)
# Deleting node with key 8
root = deletenode(root, 8)
print()
print("Deleting node with key 8: ", end = "")
levelorder(root)
# Deleting node with key 1
root = deletenode(root, 1)
print()
print("Deleting node with key 1: ", end = "")
levelorder(root)
# Deleting node with key 4
root = deletenode(root, 4)
print()
print("Deleting node with key 4: ", end = "")
levelorder(root)
# This code is contributed by mohit kumar 29
C#
// C# implementation to delete a node
// in Binary Tree using Level Order Traversal
using System;
using System.Collections.Generic;
// Binary Tree
public class TreeNode
{
public int data;
public TreeNode left = null;
public TreeNode right = null;
public TreeNode(int data)
{
this.data = data;
}
}
public class BinaryTreeDeleteKNode{
public TreeNode insert(TreeNode root,
int value)
{
if (root == null)
{
root = new TreeNode(value);
return root;
}
// Do level order traversal and add
// node to first null
Queue<TreeNode> q = new Queue<TreeNode>();
q.Enqueue(root);
while (q.Count!=0)
{
TreeNode tn = q.Dequeue();
if (tn.left != null)
{
q.Enqueue(tn.left);
}
else
{
tn.left = new TreeNode(value);
return root;
}
if (tn.right != null)
{
q.Enqueue(tn.right);
}
else
{
tn.right = new TreeNode(value);
return root;
}
}
return root;
}
// Function for Level Order
// Traversal of Binary Tree
public void levelOrder(TreeNode root)
{
if (root == null)
{
Console.WriteLine("Tree is empty!!");
}
// Queue to store the nodes
// in a level
Queue<TreeNode> q = new Queue<TreeNode>();
q.Enqueue(root);
// Loop to Traverse the Binary
// Tree in Level Order
while (q.Count!=0)
{
TreeNode tn = q.Dequeue();
Console.Write(tn.data + " ");
if (tn.left != null)
q.Enqueue(tn.left);
if (tn.right != null)
q.Enqueue(tn.right);
}
}
// Function to delete node node with value K
public TreeNode deleteIn(TreeNode root, int k)
{
if (root == null)
return root;
// Do level order traversal if node found
// with the value k then select that node
// keep traversal till we find deepest
// node with empty value keep track of
// the parent node of the deepest node
TreeNode searchedNode = null;
TreeNode tn = null;
Queue<TreeNode> q = new Queue<TreeNode>();
TreeNode deepestNodeParent = null;
q.Enqueue(root);
while (q.Count!=0)
{
bool isParent = false;
tn = q.Dequeue();
if (searchedNode == null && tn.data == k)
{
searchedNode = tn;
}
if (tn.left != null)
{
q.Enqueue(tn.left);
isParent = true;
}
if (tn.right != null)
{
q.Enqueue(tn.right);
isParent = true;
}
if (isParent) deepestNodeParent = tn;
}
if (searchedNode == null)
{
Console.Write("Node with value '" + k +
"' not exists.");
return root;
}
searchedNode.data = tn.data;
if (deepestNodeParent != null &&
deepestNodeParent.left != null &&
deepestNodeParent.left.data == tn.data)
{
deepestNodeParent.left = null;
}
else
{
deepestNodeParent.right = null;
}
return root;
}
// Driver Code
public static void Main()
{
TreeNode node = null;
BinaryTreeDeleteKNode binaryTreeDeleteKNode = new BinaryTreeDeleteKNode();
// Construction of Tree
node = binaryTreeDeleteKNode.insert(node, 1);
node = binaryTreeDeleteKNode.insert(node, 8);
node = binaryTreeDeleteKNode.insert(node, 3);
node = binaryTreeDeleteKNode.insert(node, 4);
node = binaryTreeDeleteKNode.insert(node, 5);
node = binaryTreeDeleteKNode.insert(node, 6);
node = binaryTreeDeleteKNode.insert(node, 7);
Console.Write("Original Tree: ");
binaryTreeDeleteKNode.levelOrder(node);
// Deleting node with key 8
node = binaryTreeDeleteKNode.deleteIn(node,8);
Console.Write("\nDeleting node with key 8: ");
binaryTreeDeleteKNode.levelOrder(node);
// Deleting node with key 1
node = binaryTreeDeleteKNode.deleteIn(node,1);
Console.Write("\nDeleting node with key 1: ");
binaryTreeDeleteKNode.levelOrder(node);
// Deleting node with key 4
node = binaryTreeDeleteKNode.deleteIn(node,4);
Console.Write("\nDeleting node with key 4: ");
binaryTreeDeleteKNode.levelOrder(node);
}
}
// This code is contributed by jana_sayantan.
Javascript
<script>
// Javascript implementation to delete a node
// in Binary Tree using Level Order Traversal
// Binary Tree
class TreeNode
{
constructor(data)
{
this.data=data;
this.left=this.right=null;
}
}
function insert(root,value)
{
if (root == null)
{
root = new TreeNode(value);
return root;
}
// Do level order traversal and add
// node to first null
let q = [];
q.push(root);
while (q.length!=0)
{
let tn = q.shift();
if (tn.left != null)
{
q.push(tn.left);
}
else
{
tn.left = new TreeNode(value);
return root;
}
if (tn.right != null)
{
q.push(tn.right);
}
else
{
tn.right = new TreeNode(value);
return root;
}
}
return root;
}
// Function for Level Order
// Traversal of Binary Tree
function levelOrder(root)
{
if (root == null)
{
document.write("Tree is empty!!<br>");
}
// Queue to store the nodes
// in a level
let q = [];
q.push(root);
// Loop to Traverse the Binary
// Tree in Level Order
while (q.length!=0)
{
let tn = q.shift();
document.write(tn.data + " ");
if (tn.left != null)
q.push(tn.left);
if (tn.right != null)
q.push(tn.right);
}
}
// Function to delete node node with value K
function deleteIn(root,k)
{
if (root == null)
return root;
// Do level order traversal if node found
// with the value k then select that node
// keep traversal till we find deepest
// node with empty value keep track of
// the parent node of the deepest node
let searchedNode = null;
let tn = null;
let q = [];
let deepestNodeParent = null;
q.push(root);
while (q.length!=0)
{
let isParent = false;
tn = q.shift();
if (searchedNode == null && tn.data == k)
{
searchedNode = tn;
}
if (tn.left != null)
{
q.push(tn.left);
isParent = true;
}
if (tn.right != null)
{
q.push(tn.right);
isParent = true;
}
if (isParent) deepestNodeParent = tn;
}
if (searchedNode == null)
{
document.write("Node with value '" + k +
"' not exists.");
return root;
}
searchedNode.data = tn.data;
if (deepestNodeParent != null &&
deepestNodeParent.left != null &&
deepestNodeParent.left.data == tn.data)
{
deepestNodeParent.left = null;
}
else
{
deepestNodeParent.right = null;
}
return root;
}
// Driver code
let node = null;
// Construction of Tree
node = insert(node, 1);
node = insert(node, 8);
node = insert(node, 3);
node = insert(node, 4);
node = insert(node, 5);
node = insert(node, 6);
node = insert(node, 7);
document.write("Original Tree: ");
levelOrder(node);
// Deleting node with key 8
node = deleteIn(node,8);
document.write("<br>Deleting node with key 8: ");
levelOrder(node);
// Deleting node with key 1
node = deleteIn(node,1);
document.write("<br>Deleting node with key 1: ");
levelOrder(node);
// Deleting node with key 4
node = deleteIn(node,4);
document.write("<br>Deleting node with key 4: ");
levelOrder(node);
// This code is contributed by unknown2108
</script>
Producción:
Original Tree: 1 8 3 4 5 6 7 Deleting node with key 8: 1 7 3 4 5 6 Deleting node with key 1: 6 7 3 4 5 Deleting node with key 4: 6 7 3 5
Publicación traducida automáticamente
Artículo escrito por codingbuff y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA


