Se recomienda hacer referencia a las siguientes publicaciones como requisito previo para esta publicación.
Árbol B | Juego 1 (Introducción)
B-Tree | Conjunto 2 (Insertar)
B-Tree es un tipo de árbol de búsqueda multidireccional. Por lo tanto, si no está familiarizado con los árboles de búsqueda multidireccional en general, es mejor que eche un vistazo a esta videoconferencia del IIT-Delhi antes de continuar. Una vez que tenga claros los conceptos básicos de un árbol de búsqueda multidireccional, las operaciones de B-Tree serán más fáciles de entender.
La fuente de la siguiente explicación y algoritmo es Introducción a los algoritmos, 3.ª edición, de Clifford Stein, Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest
Proceso de eliminación:
La eliminación de un árbol B es más complicada que la inserción, porque podemos eliminar una clave de cualquier Node, no solo una hoja, y cuando eliminamos una clave de un Node interno, tendremos que reorganizar los elementos secundarios del Node.
Al igual que en la inserción, debemos asegurarnos de que la eliminación no viole las propiedades del árbol B. Así como teníamos que asegurarnos de que un Node no se hiciera demasiado grande debido a la inserción, debemos asegurarnos de que un Node no se hiciera demasiado pequeño durante la eliminación (excepto que se permite que la raíz tenga menos del número mínimo t-1 de llaves). Así como un algoritmo de inserción simple podría tener que hacer una copia de seguridad si un Node en la ruta donde se iba a insertar la clave estaba lleno, un enfoque simple para la eliminación podría tener que hacer una copia de seguridad si un Node (que no sea la raíz) a lo largo de la ruta a donde se va a borrar la clave tiene el número mínimo de claves.
El procedimiento de eliminación elimina la clave k del subárbol enraizado en x. Este procedimiento garantiza que siempre que se llame a sí mismo recursivamente en un Node x, el número de claves en x sea al menos el grado mínimo t. Tenga en cuenta que esta condición requiere una clave más que el mínimo requerido por las condiciones habituales del árbol B, por lo que a veces puede ser necesario mover una clave a un Node secundario antes de que la recursividad descienda a ese elemento secundario. Esta condición fortalecida nos permite eliminar una clave del árbol en un paso hacia abajo sin tener que «retroceder» (con una excepción, que explicaremos). Debe interpretar la siguiente especificación para la eliminación de un árbol B con el entendimiento de que si el Node raíz x alguna vez se convierte en un Node interno sin claves (esta situación puede ocurrir en los casos 2c y 3b, entonces eliminamos x, y el único hijo x de x .
Esbozamos cómo funciona la eliminación con varios casos de eliminación de claves de un árbol B.
1. Si la clave k está en el Node x y x es una hoja, elimine la clave k de x.
2. Si la clave k está en el Node x y x es un Node interno, haga lo siguiente.
a) Si el hijo y que precede a k en el Node x tiene al menos t claves, entonces busque el predecesor k0 de k en el subárbol con raíz en y. Elimine recursivamente k0 y reemplace k por k0 en x. (Podemos encontrar k0 y borrarlo en un solo paso hacia abajo.)
b)Si y tiene menos claves que t, entonces, simétricamente, examine el hijo z que sigue a k en el Node x. Si z tiene al menos t claves, busque el sucesor k0 de k en el subárbol con raíz en z. Elimine recursivamente k0 y reemplace k por k0 en x. (Podemos encontrar k0 y eliminarlo en un solo paso hacia abajo.)
c) De lo contrario, si tanto y como z tienen solo t-1 claves, combine k y todo z en y, de modo que x pierda tanto k como el puntero a z e y ahora contienen claves 2t-1. Luego libere z y elimine recursivamente k de y.
3.Si la clave k no está presente en el Node interno x, determine la raíz xc(i) del subárbol apropiado que debe contener k, si es que k está en el árbol. Si xc(i) tiene solo t-1 claves, ejecute el paso 3a o 3b según sea necesario para garantizar que descendemos a un Node que contiene al menos t claves. Luego termine recursando al hijo apropiado de x.
a) Si xc(i) tiene solo t-1 claves pero tiene un hermano inmediato con al menos t claves, dé a xc(i) una clave adicional moviendo una clave de x hacia abajo a xc(i), moviendo una clave de xc (i) el hermano inmediato izquierdo o derecho de ‘s hacia arriba en x, y moviendo el puntero secundario apropiado del hermano a xc (i).
b)Si xc(i) y los dos hermanos inmediatos de xc(i) tienen claves t-1, combine xc(i) con un hermano, lo que implica mover una clave de x hacia abajo al nuevo Node fusionado para convertirse en la clave mediana para ese Node.
Dado que la mayoría de las claves en un árbol B están en las hojas, las operaciones de eliminación se usan con mayor frecuencia para eliminar claves de las hojas. El procedimiento de borrado recursivo luego actúa en un paso hacia abajo a través del árbol, sin tener que retroceder. Sin embargo, al eliminar una clave en un Node interno, el procedimiento realiza un recorrido descendente por el árbol, pero es posible que tenga que volver al Node del que se eliminó la clave para reemplazar la clave con su predecesora o sucesora (casos 2a y 2b).
Las siguientes figuras explican el proceso de borrado.

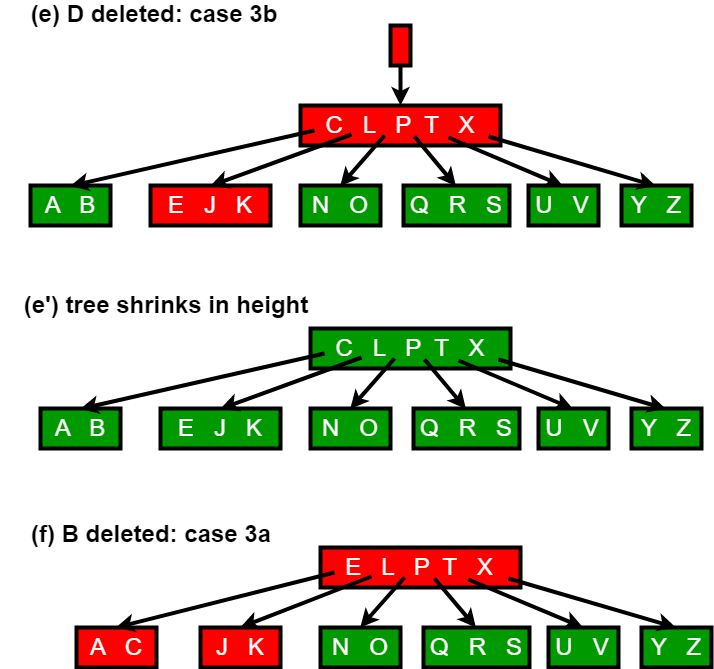
Implementación:
A continuación se muestra la implementación en C++ del proceso de eliminación.
C++
#include<iostream>
using namespace std;
// A BTree node
class BTreeNode
{
int *keys; // An array of keys
int t; // Minimum degree (defines the range for number of keys)
BTreeNode **C; // An array of child pointers
int n; // Current number of keys
bool leaf; // Is true when node is leaf. Otherwise false
public:
BTreeNode(int _t, bool _leaf); // Constructor
// A function to traverse all nodes in a subtree rooted with this node
void traverse();
// A function to search a key in subtree rooted with this node.
BTreeNode *search(int k); // returns NULL if k is not present.
// A function that returns the index of the first key that is greater
// or equal to k
int findKey(int k);
// A utility function to insert a new key in the subtree rooted with
// this node. The assumption is, the node must be non-full when this
// function is called
void insertNonFull(int k);
// A utility function to split the child y of this node. i is index
// of y in child array C[]. The Child y must be full when this
// function is called
void splitChild(int i, BTreeNode *y);
// A wrapper function to remove the key k in subtree rooted with
// this node.
void remove(int k);
// A function to remove the key present in idx-th position in
// this node which is a leaf
void removeFromLeaf(int idx);
// A function to remove the key present in idx-th position in
// this node which is a non-leaf node
void removeFromNonLeaf(int idx);
// A function to get the predecessor of the key- where the key
// is present in the idx-th position in the node
int getPred(int idx);
// A function to get the successor of the key- where the key
// is present in the idx-th position in the node
int getSucc(int idx);
// A function to fill up the child node present in the idx-th
// position in the C[] array if that child has less than t-1 keys
void fill(int idx);
// A function to borrow a key from the C[idx-1]-th node and place
// it in C[idx]th node
void borrowFromPrev(int idx);
// A function to borrow a key from the C[idx+1]-th node and place it
// in C[idx]th node
void borrowFromNext(int idx);
// A function to merge idx-th child of the node with (idx+1)th child of
// the node
void merge(int idx);
// Make BTree friend of this so that we can access private members of
// this class in BTree functions
friend class BTree;
};
class BTree
{
BTreeNode *root; // Pointer to root node
int t; // Minimum degree
public:
// Constructor (Initializes tree as empty)
BTree(int _t)
{
root = NULL;
t = _t;
}
void traverse()
{
if (root != NULL) root->traverse();
}
// function to search a key in this tree
BTreeNode* search(int k)
{
return (root == NULL)? NULL : root->search(k);
}
// The main function that inserts a new key in this B-Tree
void insert(int k);
// The main function that removes a new key in thie B-Tree
void remove(int k);
};
BTreeNode::BTreeNode(int t1, bool leaf1)
{
// Copy the given minimum degree and leaf property
t = t1;
leaf = leaf1;
// Allocate memory for maximum number of possible keys
// and child pointers
keys = new int[2*t-1];
C = new BTreeNode *[2*t];
// Initialize the number of keys as 0
n = 0;
}
// A utility function that returns the index of the first key that is
// greater than or equal to k
int BTreeNode::findKey(int k)
{
int idx=0;
while (idx<n && keys[idx] < k)
++idx;
return idx;
}
// A function to remove the key k from the sub-tree rooted with this node
void BTreeNode::remove(int k)
{
int idx = findKey(k);
// The key to be removed is present in this node
if (idx < n && keys[idx] == k)
{
// If the node is a leaf node - removeFromLeaf is called
// Otherwise, removeFromNonLeaf function is called
if (leaf)
removeFromLeaf(idx);
else
removeFromNonLeaf(idx);
}
else
{
// If this node is a leaf node, then the key is not present in tree
if (leaf)
{
cout<<"The key "<<k<<" is does not exist in the tree\n";
return;
}
// The key to be removed is present in the sub-tree rooted with this node
// The flag indicates whether the key is present in the sub-tree rooted
// with the last child of this node
bool flag = ( (idx==n)? true : false );
// If the child where the key is supposed to exist has less that t keys,
// we fill that child
if (C[idx]->n < t)
fill(idx);
// If the last child has been merged, it must have merged with the previous
// child and so we recurse on the (idx-1)th child. Else, we recurse on the
// (idx)th child which now has atleast t keys
if (flag && idx > n)
C[idx-1]->remove(k);
else
C[idx]->remove(k);
}
return;
}
// A function to remove the idx-th key from this node - which is a leaf node
void BTreeNode::removeFromLeaf (int idx)
{
// Move all the keys after the idx-th pos one place backward
for (int i=idx+1; i<n; ++i)
keys[i-1] = keys[i];
// Reduce the count of keys
n--;
return;
}
// A function to remove the idx-th key from this node - which is a non-leaf node
void BTreeNode::removeFromNonLeaf(int idx)
{
int k = keys[idx];
// If the child that precedes k (C[idx]) has atleast t keys,
// find the predecessor 'pred' of k in the subtree rooted at
// C[idx]. Replace k by pred. Recursively delete pred
// in C[idx]
if (C[idx]->n >= t)
{
int pred = getPred(idx);
keys[idx] = pred;
C[idx]->remove(pred);
}
// If the child C[idx] has less that t keys, examine C[idx+1].
// If C[idx+1] has atleast t keys, find the successor 'succ' of k in
// the subtree rooted at C[idx+1]
// Replace k by succ
// Recursively delete succ in C[idx+1]
else if (C[idx+1]->n >= t)
{
int succ = getSucc(idx);
keys[idx] = succ;
C[idx+1]->remove(succ);
}
// If both C[idx] and C[idx+1] has less that t keys,merge k and all of C[idx+1]
// into C[idx]
// Now C[idx] contains 2t-1 keys
// Free C[idx+1] and recursively delete k from C[idx]
else
{
merge(idx);
C[idx]->remove(k);
}
return;
}
// A function to get predecessor of keys[idx]
int BTreeNode::getPred(int idx)
{
// Keep moving to the right most node until we reach a leaf
BTreeNode *cur=C[idx];
while (!cur->leaf)
cur = cur->C[cur->n];
// Return the last key of the leaf
return cur->keys[cur->n-1];
}
int BTreeNode::getSucc(int idx)
{
// Keep moving the left most node starting from C[idx+1] until we reach a leaf
BTreeNode *cur = C[idx+1];
while (!cur->leaf)
cur = cur->C[0];
// Return the first key of the leaf
return cur->keys[0];
}
// A function to fill child C[idx] which has less than t-1 keys
void BTreeNode::fill(int idx)
{
// If the previous child(C[idx-1]) has more than t-1 keys, borrow a key
// from that child
if (idx!=0 && C[idx-1]->n>=t)
borrowFromPrev(idx);
// If the next child(C[idx+1]) has more than t-1 keys, borrow a key
// from that child
else if (idx!=n && C[idx+1]->n>=t)
borrowFromNext(idx);
// Merge C[idx] with its sibling
// If C[idx] is the last child, merge it with its previous sibling
// Otherwise merge it with its next sibling
else
{
if (idx != n)
merge(idx);
else
merge(idx-1);
}
return;
}
// A function to borrow a key from C[idx-1] and insert it
// into C[idx]
void BTreeNode::borrowFromPrev(int idx)
{
BTreeNode *child=C[idx];
BTreeNode *sibling=C[idx-1];
// The last key from C[idx-1] goes up to the parent and key[idx-1]
// from parent is inserted as the first key in C[idx]. Thus, the loses
// sibling one key and child gains one key
// Moving all key in C[idx] one step ahead
for (int i=child->n-1; i>=0; --i)
child->keys[i+1] = child->keys[i];
// If C[idx] is not a leaf, move all its child pointers one step ahead
if (!child->leaf)
{
for(int i=child->n; i>=0; --i)
child->C[i+1] = child->C[i];
}
// Setting child's first key equal to keys[idx-1] from the current node
child->keys[0] = keys[idx-1];
// Moving sibling's last child as C[idx]'s first child
if(!child->leaf)
child->C[0] = sibling->C[sibling->n];
// Moving the key from the sibling to the parent
// This reduces the number of keys in the sibling
keys[idx-1] = sibling->keys[sibling->n-1];
child->n += 1;
sibling->n -= 1;
return;
}
// A function to borrow a key from the C[idx+1] and place
// it in C[idx]
void BTreeNode::borrowFromNext(int idx)
{
BTreeNode *child=C[idx];
BTreeNode *sibling=C[idx+1];
// keys[idx] is inserted as the last key in C[idx]
child->keys[(child->n)] = keys[idx];
// Sibling's first child is inserted as the last child
// into C[idx]
if (!(child->leaf))
child->C[(child->n)+1] = sibling->C[0];
//The first key from sibling is inserted into keys[idx]
keys[idx] = sibling->keys[0];
// Moving all keys in sibling one step behind
for (int i=1; i<sibling->n; ++i)
sibling->keys[i-1] = sibling->keys[i];
// Moving the child pointers one step behind
if (!sibling->leaf)
{
for(int i=1; i<=sibling->n; ++i)
sibling->C[i-1] = sibling->C[i];
}
// Increasing and decreasing the key count of C[idx] and C[idx+1]
// respectively
child->n += 1;
sibling->n -= 1;
return;
}
// A function to merge C[idx] with C[idx+1]
// C[idx+1] is freed after merging
void BTreeNode::merge(int idx)
{
BTreeNode *child = C[idx];
BTreeNode *sibling = C[idx+1];
// Pulling a key from the current node and inserting it into (t-1)th
// position of C[idx]
child->keys[t-1] = keys[idx];
// Copying the keys from C[idx+1] to C[idx] at the end
for (int i=0; i<sibling->n; ++i)
child->keys[i+t] = sibling->keys[i];
// Copying the child pointers from C[idx+1] to C[idx]
if (!child->leaf)
{
for(int i=0; i<=sibling->n; ++i)
child->C[i+t] = sibling->C[i];
}
// Moving all keys after idx in the current node one step before -
// to fill the gap created by moving keys[idx] to C[idx]
for (int i=idx+1; i<n; ++i)
keys[i-1] = keys[i];
// Moving the child pointers after (idx+1) in the current node one
// step before
for (int i=idx+2; i<=n; ++i)
C[i-1] = C[i];
// Updating the key count of child and the current node
child->n += sibling->n+1;
n--;
// Freeing the memory occupied by sibling
delete(sibling);
return;
}
// The main function that inserts a new key in this B-Tree
void BTree::insert(int k)
{
// If tree is empty
if (root == NULL)
{
// Allocate memory for root
root = new BTreeNode(t, true);
root->keys[0] = k; // Insert key
root->n = 1; // Update number of keys in root
}
else // If tree is not empty
{
// If root is full, then tree grows in height
if (root->n == 2*t-1)
{
// Allocate memory for new root
BTreeNode *s = new BTreeNode(t, false);
// Make old root as child of new root
s->C[0] = root;
// Split the old root and move 1 key to the new root
s->splitChild(0, root);
// New root has two children now. Decide which of the
// two children is going to have new key
int i = 0;
if (s->keys[0] < k)
i++;
s->C[i]->insertNonFull(k);
// Change root
root = s;
}
else // If root is not full, call insertNonFull for root
root->insertNonFull(k);
}
}
// A utility function to insert a new key in this node
// The assumption is, the node must be non-full when this
// function is called
void BTreeNode::insertNonFull(int k)
{
// Initialize index as index of rightmost element
int i = n-1;
// If this is a leaf node
if (leaf == true)
{
// The following loop does two things
// a) Finds the location of new key to be inserted
// b) Moves all greater keys to one place ahead
while (i >= 0 && keys[i] > k)
{
keys[i+1] = keys[i];
i--;
}
// Insert the new key at found location
keys[i+1] = k;
n = n+1;
}
else // If this node is not leaf
{
// Find the child which is going to have the new key
while (i >= 0 && keys[i] > k)
i--;
// See if the found child is full
if (C[i+1]->n == 2*t-1)
{
// If the child is full, then split it
splitChild(i+1, C[i+1]);
// After split, the middle key of C[i] goes up and
// C[i] is splitted into two. See which of the two
// is going to have the new key
if (keys[i+1] < k)
i++;
}
C[i+1]->insertNonFull(k);
}
}
// A utility function to split the child y of this node
// Note that y must be full when this function is called
void BTreeNode::splitChild(int i, BTreeNode *y)
{
// Create a new node which is going to store (t-1) keys
// of y
BTreeNode *z = new BTreeNode(y->t, y->leaf);
z->n = t - 1;
// Copy the last (t-1) keys of y to z
for (int j = 0; j < t-1; j++)
z->keys[j] = y->keys[j+t];
// Copy the last t children of y to z
if (y->leaf == false)
{
for (int j = 0; j < t; j++)
z->C[j] = y->C[j+t];
}
// Reduce the number of keys in y
y->n = t - 1;
// Since this node is going to have a new child,
// create space of new child
for (int j = n; j >= i+1; j--)
C[j+1] = C[j];
// Link the new child to this node
C[i+1] = z;
// A key of y will move to this node. Find location of
// new key and move all greater keys one space ahead
for (int j = n-1; j >= i; j--)
keys[j+1] = keys[j];
// Copy the middle key of y to this node
keys[i] = y->keys[t-1];
// Increment count of keys in this node
n = n + 1;
}
// Function to traverse all nodes in a subtree rooted with this node
void BTreeNode::traverse()
{
// There are n keys and n+1 children, traverse through n keys
// and first n children
int i;
for (i = 0; i < n; i++)
{
// If this is not leaf, then before printing key[i],
// traverse the subtree rooted with child C[i].
if (leaf == false)
C[i]->traverse();
cout << " " << keys[i];
}
// Print the subtree rooted with last child
if (leaf == false)
C[i]->traverse();
}
// Function to search key k in subtree rooted with this node
BTreeNode *BTreeNode::search(int k)
{
// Find the first key greater than or equal to k
int i = 0;
while (i < n && k > keys[i])
i++;
// If the found key is equal to k, return this node
if (keys[i] == k)
return this;
// If key is not found here and this is a leaf node
if (leaf == true)
return NULL;
// Go to the appropriate child
return C[i]->search(k);
}
void BTree::remove(int k)
{
if (!root)
{
cout << "The tree is empty\n";
return;
}
// Call the remove function for root
root->remove(k);
// If the root node has 0 keys, make its first child as the new root
// if it has a child, otherwise set root as NULL
if (root->n==0)
{
BTreeNode *tmp = root;
if (root->leaf)
root = NULL;
else
root = root->C[0];
// Free the old root
delete tmp;
}
return;
}
// Driver program to test above functions
int main()
{
BTree t(3); // A B-Tree with minimum degree 3
t.insert(1);
t.insert(3);
t.insert(7);
t.insert(10);
t.insert(11);
t.insert(13);
t.insert(14);
t.insert(15);
t.insert(18);
t.insert(16);
t.insert(19);
t.insert(24);
t.insert(25);
t.insert(26);
t.insert(21);
t.insert(4);
t.insert(5);
t.insert(20);
t.insert(22);
t.insert(2);
t.insert(17);
t.insert(12);
t.insert(6);
cout << "Traversal of tree constructed is\n";
t.traverse();
cout << endl;
t.remove(6);
cout << "Traversal of tree after removing 6\n";
t.traverse();
cout << endl;
t.remove(13);
cout << "Traversal of tree after removing 13\n";
t.traverse();
cout << endl;
t.remove(7);
cout << "Traversal of tree after removing 7\n";
t.traverse();
cout << endl;
t.remove(4);
cout << "Traversal of tree after removing 4\n";
t.traverse();
cout << endl;
t.remove(2);
cout << "Traversal of tree after removing 2\n";
t.traverse();
cout << endl;
t.remove(16);
cout << "Traversal of tree after removing 16\n";
t.traverse();
cout << endl;
return 0;
}
Producción:
Traversal of tree constructed is 1 2 3 4 5 6 7 10 11 12 13 14 15 16 17 18 19 20 21 22 24 25 26 Traversal of tree after removing 6 1 2 3 4 5 7 10 11 12 13 14 15 16 17 18 19 20 21 22 24 25 26 Traversal of tree after removing 13 1 2 3 4 5 7 10 11 12 14 15 16 17 18 19 20 21 22 24 25 26 Traversal of tree after removing 7 1 2 3 4 5 10 11 12 14 15 16 17 18 19 20 21 22 24 25 26 Traversal of tree after removing 4 1 2 3 5 10 11 12 14 15 16 17 18 19 20 21 22 24 25 26 Traversal of tree after removing 2 1 3 5 10 11 12 14 15 16 17 18 19 20 21 22 24 25 26 Traversal of tree after removing 16 1 3 5 10 11 12 14 15 17 18 19 20 21 22 24 25 26
Este artículo es una contribución de Balasubramanian.N . Escriba comentarios si encuentra algo incorrecto o si desea compartir más información sobre el tema tratado anteriormente.
Publicación traducida automáticamente
Artículo escrito por GeeksforGeeks-1 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA