Dado un árbol binario y un número entero K , la tarea es eliminar Nodes del árbol dado de modo que la suma de todos los Nodes de todos los caminos restantes de la raíz a la hoja sea al menos K .
Ejemplos:
Entrada: K = 27
Salida: 5 4 8 5 6 11
Explicación:
A continuación se muestran los caminos cuya suma es menor que 27:
- 5 -> 3 -> 9: Suma de ruta = 5 + 3 + 9 = 17.
- 5 -> 4 -> 9: Suma de ruta = 5 + 4 + 9 = 18.
- 5 -> 4 -> 8 -> 5 -> 2: Suma de ruta = 5 + 4 + 8 + 5 + 2 = 24.
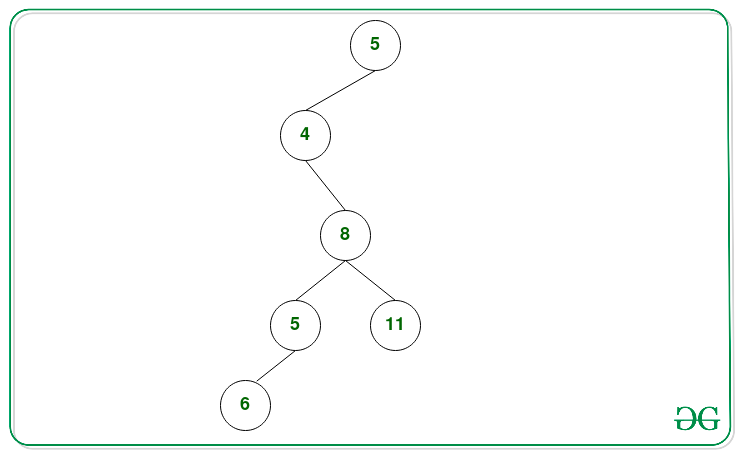
A continuación se muestra el árbol después de eliminar los Nodes requeridos de modo que la suma de todas las rutas sea al menos 27:
Entrada: K = 10
Salida: 2 1 8 12 14 7 10
Enfoque: La idea es usar la recursividad y realizar el Postorder Traversal y eliminar aquellos Nodes cuya suma a la suma de la ruta sea menor que K . A continuación se muestran los pasos:
- Realice el Post Order Traversal en el Árbol dado y durante este recorrido pase la suma de todos los Nodes desde el Node raíz a cada Node.
- Durante el recorrido, si alcanzamos el Node hoja, verificamos si la suma de todos los Nodes hasta ese Node es menor que K. . Si se determina que es cierto, elimine ese Node devolviendo el Node NULL de ese Node.
- Repita el paso anterior para cada encuentro de Nodes hoja en el árbol de actualización.
- Después de los pasos anteriores, imprima el Preorder Traversal del Tree modificado.
A continuación se muestra la implementación del enfoque anterior:
C++
// C++ program for the above approach
#include <bits/stdc++.h>
using namespace std;
// Tree Node Class
struct Node
{
int data;
Node *left;
Node *right;
Node(int x)
{
data = x;
left = right = NULL;
}
};
// Utility function that deletes nodes
// from the Tree such that every root
// to leaf path sum is at least K
Node *removePathLessThanK(Node *node, int K,
int sum)
{
// Base Case
if (node == NULL)
{
return NULL;
}
// Recurse to the left
if (node->left != NULL)
{
node->left = removePathLessThanK(
node->left, K,
sum + node->left->data);
}
// Recurse to the right
if (node->right != NULL)
{
node->right = removePathLessThanK(
node->right, K,
sum + node->right->data);
}
// Check path sum at leaf node
// is lesser than K, return NULL
if (node->left == NULL &&
node->right == NULL && sum < K)
{
node = NULL;
return node;
}
// Otherwise return the
// current node as it is
return node;
}
// Function to print the preorder
// traversal of the Tree
void viewTree(Node *node)
{
// If node is not NULL
if (node != NULL)
{
// Print the node
cout << node->data << " ";
// Left and Right Traversal
viewTree(node->left);
viewTree(node->right);
}
}
// Function that deletes the nodes
// from the Tree such that every root
// to leaf path sum is at least K
void removePathLessThanKUtil(Node *node, int K,
int sum)
{
// Function Call to delete Nodes
Node *result = removePathLessThanK(node, K, sum);
// Preorder Traversal of the
// modified Tree
viewTree(result);
}
// Driver Code
int main()
{
// Given sum K
int K = 27;
// Given Binary Tree
Node *root = NULL;
root = new Node(5);
root->right = new Node(3);
root->left = new Node(4);
root->left->left = new Node(9);
root->right->right = new Node(9);
root->left->right = new Node(8);
root->left->right->right = new Node(11);
root->left->right->left = new Node(5);
root->left->right->left->left = new Node(6);
root->left->right->left->right = new Node(2);
root->right->right->right = new Node(4);
// Function Call
removePathLessThanKUtil(root, K, root->data);
}
// This code is contributed by mohit kumar 29
Java
// Java program for the above approach
import java.io.*;
import java.util.*;
// Tree Node Class
class Node {
int data;
Node left;
Node right;
}
class path {
// Function to insert node in the
// given Binary Tree
public Node insert(int val)
{
Node n = new Node();
n.data = val;
n.left = null;
n.right = null;
return n;
}
// Utility function that deletes nodes
// from the Tree such that every root
// to leaf path sum is at least K
public Node removePathLessThanK(
Node node, int K, int sum)
{
// Base Case
if (node == null) {
return null;
}
// Recurse to the left
if (node.left != null) {
node.left
= removePathLessThanK(
node.left, K,
sum + node.left.data);
}
// Recurse to the right
if (node.right != null) {
node.right
= removePathLessThanK(
node.right, K,
sum + node.right.data);
}
// Check path sum at leaf node
// is lesser than K, return NULL
if (node.left == null
&& node.right == null
&& sum < K) {
node = null;
return node;
}
// Otherwise return the
// current node as it is
return node;
}
// Function to print the preorder
// traversal of the Tree
public void viewTree(Node node)
{
// If node is not NULL
if (node != null) {
// Print the node
System.out.print(node.data + " ");
// Left and Right Traversal
viewTree(node.left);
viewTree(node.right);
}
}
// Function that deletes the nodes
// from the Tree such that every root
// to leaf path sum is at least K
public void removePathLessThanKUtil(
Node node, int K, int sum)
{
// Function Call to delete Nodes
Node result = removePathLessThanK(
node, K, sum);
// Preorder Traversal of the
// modified Tree
viewTree(result);
}
}
// Driver Code
class GFG {
// Driver Code
public static void main(String[] args)
{
// Given sum K
int K = 27;
// Object of class path
path b = new path();
// Given Binary Tree
Node root = null;
root = b.insert(5);
root.right = b.insert(3);
root.left = b.insert(4);
root.left.left = b.insert(9);
root.right.right = b.insert(9);
root.left.right = b.insert(8);
root.left.right.right = b.insert(11);
root.left.right.left = b.insert(5);
root.left.right.left.left = b.insert(6);
root.left.right.left.right = b.insert(2);
root.right.right.right = b.insert(4);
// Function Call
b.removePathLessThanKUtil(
root, K, root.data);
}
}
Python3
# Python3 program for the above approach # Tree Node Class class newNode: def __init__(self, x): self.data = x self.left = None self.right = None # Utility function that deletes nodes # from the Tree such that every root # to leaf path sum is at least K def removePathLessThanK(node, K, sum): # Base Case if (node == None): return None # Recurse to the left if (node.left != None): node.left = removePathLessThanK( node.left, K, sum + node.left.data) # Recurse to the right if (node.right != None): node.right = removePathLessThanK( node.right, K, sum + node.right.data) # Check path sum at leaf node # is lesser than K, return None if (node.left == None and node.right == None and sum < K): node = None return node # Otherwise return the # current node as it is return node # Function to print the preorder # traversal of the Tree def viewTree(node): # If node is not None if (node != None): # Print the node print(node.data, end = " ") # Left and Right Traversal viewTree(node.left) viewTree(node.right) # Function that deletes the nodes # from the Tree such that every root # to leaf path sum is at least K def removePathLessThanKUtil(node, K, sum): # Function Call to delete Nodes result = removePathLessThanK(node, K, sum) # Preorder Traversal of the # modified Tree viewTree(result) # Driver Code if __name__ == '__main__': # Given sum K K = 27 # Given Binary Tree root = None root = newNode(5) root.right = newNode(3) root.left = newNode(4) root.left.left = newNode(9) root.right.right = newNode(9) root.left.right = newNode(8) root.left.right.right = newNode(11) root.left.right.left = newNode(5) root.left.right.left.left = newNode(6) root.left.right.left.right = newNode(2) root.right.right.right = newNode(4) # Function Call removePathLessThanKUtil(root, K, root.data) # This code is contributed by SURENDRA_GANGWAR
C#
// C# program for the above approach
using System;
// Tree Node Class
public class Node
{
public int data;
public Node left;
public Node right;
}
class path{
// Function to insert node in the
// given Binary Tree
public Node insert(int val)
{
Node n = new Node();
n.data = val;
n.left = null;
n.right = null;
return n;
}
// Utility function that deletes nodes
// from the Tree such that every root
// to leaf path sum is at least K
public Node removePathLessThanK(Node node,
int K, int sum)
{
// Base Case
if (node == null)
{
return null;
}
// Recurse to the left
if (node.left != null)
{
node.left = removePathLessThanK(
node.left, K,
sum + node.left.data);
}
// Recurse to the right
if (node.right != null)
{
node.right = removePathLessThanK(
node.right, K,
sum + node.right.data);
}
// Check path sum at leaf node
// is lesser than K, return NULL
if (node.left == null &&
node.right == null && sum < K)
{
node = null;
return node;
}
// Otherwise return the
// current node as it is
return node;
}
// Function to print the preorder
// traversal of the Tree
public void viewTree(Node node)
{
// If node is not NULL
if (node != null)
{
// Print the node
Console.Write(node.data + " ");
// Left and Right Traversal
viewTree(node.left);
viewTree(node.right);
}
}
// Function that deletes the nodes
// from the Tree such that every root
// to leaf path sum is at least K
public void removePathLessThanKUtil(Node node,
int K, int sum)
{
// Function Call to delete Nodes
Node result = removePathLessThanK(
node, K, sum);
// Preorder Traversal of the
// modified Tree
viewTree(result);
}
}
// Driver Code
class GFG{
// Driver Code
public static void Main(String[] args)
{
// Given sum K
int K = 27;
// Object of class path
path b = new path();
// Given Binary Tree
Node root = null;
root = b.insert(5);
root.right = b.insert(3);
root.left = b.insert(4);
root.left.left = b.insert(9);
root.right.right = b.insert(9);
root.left.right = b.insert(8);
root.left.right.right = b.insert(11);
root.left.right.left = b.insert(5);
root.left.right.left.left = b.insert(6);
root.left.right.left.right = b.insert(2);
root.right.right.right = b.insert(4);
// Function Call
b.removePathLessThanKUtil(
root, K, root.data);
}
}
// This code is contributed by Princi Singh
Javascript
<script>
// Javascript program for the above approach
// Tree Node Class
class Node
{
constructor(val)
{
this.left = null;
this.right = null;
this.data = val;
}
}
// Function to insert node in the
// given Binary Tree
function insert(val)
{
let n = new Node(val);
return n;
}
// Utility function that deletes nodes
// from the Tree such that every root
// to leaf path sum is at least K
function removePathLessThanK(node, K, sum)
{
// Base Case
if (node == null)
{
return null;
}
// Recurse to the left
if (node.left != null)
{
node.left = removePathLessThanK(
node.left, K,
sum + node.left.data);
}
// Recurse to the right
if (node.right != null)
{
node.right = removePathLessThanK(
node.right, K,
sum + node.right.data);
}
// Check path sum at leaf node
// is lesser than K, return NULL
if (node.left == null &&
node.right == null &&
sum < K)
{
node = null;
return node;
}
// Otherwise return the
// current node as it is
return node;
}
// Function to print the preorder
// traversal of the Tree
function viewTree(node)
{
// If node is not NULL
if (node != null)
{
// Print the node
document.write(node.data + " ");
// Left and Right Traversal
viewTree(node.left);
viewTree(node.right);
}
}
// Function that deletes the nodes
// from the Tree such that every root
// to leaf path sum is at least K
function removePathLessThanKUtil(node, K, sum)
{
// Function Call to delete Nodes
let result = removePathLessThanK(node, K, sum);
// Preorder Traversal of the
// modified Tree
viewTree(result);
}
// Driver code
// Given sum K
let K = 27;
// Given Binary Tree
let root = null;
root = insert(5);
root.right = insert(3);
root.left = insert(4);
root.left.left = insert(9);
root.right.right = insert(9);
root.left.right = insert(8);
root.left.right.right = insert(11);
root.left.right.left = insert(5);
root.left.right.left.left = insert(6);
root.left.right.left.right = insert(2);
root.right.right.right = insert(4);
// Function Call
removePathLessThanKUtil(root, K, root.data);
// This code is contributed by suresh07
</script>
5 4 8 5 6 11
Complejidad de tiempo: O(N), donde N es el número de Nodes en el árbol dado.
Espacio Auxiliar: O(N)
Publicación traducida automáticamente
Artículo escrito por rohit2sahu y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA