Dado un gráfico no ponderado no dirigido con N vértices y M aristas. La tarea es encontrar dos buenos conjuntos disjuntos de vértices. Un conjunto X se llama bueno si para cada arista UV en el gráfico al menos uno de los extremos pertenece a X (es decir, U o V o tanto U como V pertenecen a X).
Si no es posible hacer tales conjuntos, imprima -1.
Ejemplos:
Aporte :
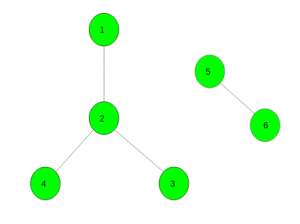
Salida: {1 3 4 5} ,{2 6}
Un buen conjunto disjunto contiene vértices {1, 3, 4, 5} y otro contiene {2, 6}.Aporte :
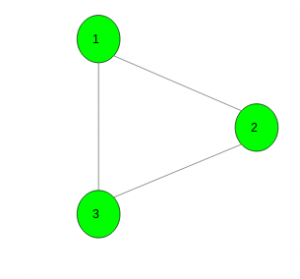
Salida: -1
Enfoque:
Una de las observaciones es que no hay borde UV que U y V estén en el mismo conjunto. Los dos buenos conjuntos forman una bipartición del gráfico, por lo que el gráfico tiene que ser bipartito. Y ser bipartito también es suficiente. Lea acerca de la bipartición aquí .
A continuación se muestra la implementación del enfoque anterior:
C++
// C++ program to find two disjoint
// good sets of vertices in a given graph
#include <bits/stdc++.h>
using namespace std;
#define N 100005
// For the graph
vector<int> gr[N], dis[2];
bool vis[N];
int colour[N];
bool bip;
// Function to add edge
void Add_edge(int x, int y)
{
gr[x].push_back(y);
gr[y].push_back(x);
}
// Bipartite function
void dfs(int x, int col)
{
vis[x] = true;
colour[x] = col;
// Check for child vertices
for (auto i : gr[x]) {
// If it is not visited
if (!vis[i])
dfs(i, col ^ 1);
// If it is already visited
else if (colour[i] == col)
bip = false;
}
}
// Function to find two disjoint
// good sets of vertices in a given graph
void goodsets(int n)
{
// Initially assume that graph is bipartite
bip = true;
// For every unvisited vertex call dfs
for (int i = 1; i <= n; i++)
if (!vis[i])
dfs(i, 0);
// If graph is not bipartite
if (!bip)
cout << -1;
else {
// Differentiate two sets
for (int i = 1; i <= n; i++)
dis[colour[i]].push_back(i);
// Print vertices belongs to both sets
for (int i = 0; i < 2; i++) {
for (int j = 0; j < dis[i].size(); j++)
cout << dis[i][j] << " ";
cout << endl;
}
}
}
// Driver code
int main()
{
int n = 6, m = 4;
// Add edges
Add_edge(1, 2);
Add_edge(2, 3);
Add_edge(2, 4);
Add_edge(5, 6);
// Function call
goodsets(n);
}
Java
// Java program to find two disjoint
// good sets of vertices in a given graph
import java.util.*;
class GFG
{
static int N = 100005;
// For the graph
@SuppressWarnings("unchecked")
static Vector<Integer>[] gr = new Vector[N],
dis = new Vector[2];
static
{
for (int i = 0; i < N; i++)
gr[i] = new Vector<>();
for (int i = 0; i < 2; i++)
dis[i] = new Vector<>();
}
static boolean[] vis = new boolean[N];
static int[] color = new int[N];
static boolean bip;
// Function to add edge
static void add_edge(int x, int y)
{
gr[x].add(y);
gr[y].add(x);
}
// Bipartite function
static void dfs(int x, int col)
{
vis[x] = true;
color[x] = col;
// Check for child vertices
for (int i : gr[x])
{
// If it is not visited
if (!vis[i])
dfs(i, col ^ 1);
// If it is already visited
else if (color[i] == col)
bip = false;
}
}
// Function to find two disjoint
// good sets of vertices in a given graph
static void goodsets(int n)
{
// Initially assume that graph is bipartite
bip = true;
// For every unvisited vertex call dfs
for (int i = 1; i <= n; i++)
if (!vis[i])
dfs(i, 0);
// If graph is not bipartite
if (!bip)
System.out.println(-1);
else
{
// Differentiate two sets
for (int i = 1; i <= n; i++)
dis[color[i]].add(i);
// Print vertices belongs to both sets
for (int i = 0; i < 2; i++)
{
for (int j = 0; j < dis[i].size(); j++)
System.out.print(dis[i].elementAt(j) + " ");
System.out.println();
}
}
}
// Driver Code
public static void main(String[] args)
{
int n = 6, m = 4;
// Add edges
add_edge(1, 2);
add_edge(2, 3);
add_edge(2, 4);
add_edge(5, 6);
// Function call
goodsets(n);
}
}
// This code is contributed by
// sanjeev2552
Python3
# Python 3 program to find two disjoint
# good sets of vertices in a given graph
N = 100005
# For the graph
gr = [[] for i in range(N)]
dis = [[] for i in range(2)]
vis = [False for i in range(N)]
colour = [0 for i in range(N)]
bip = 0
# Function to add edge
def Add_edge(x, y):
gr[x].append(y)
gr[y].append(x)
# Bipartite function
def dfs(x, col):
vis[x] = True
colour[x] = col
# Check for child vertices
for i in gr[x]:
# If it is not visited
if (vis[i] == False):
dfs(i, col ^ 1)
# If it is already visited
elif (colour[i] == col):
bip = False
# Function to find two disjoint
# good sets of vertices in a given graph
def goodsets(n):
# Initially assume that
# graph is bipartite
bip = True
# For every unvisited vertex call dfs
for i in range(1, n + 1, 1):
if (vis[i] == False):
dfs(i, 0)
# If graph is not bipartite
if (bip == 0):
print(-1)
else:
# Differentiate two sets
for i in range(1, n + 1, 1):
dis[colour[i]].append(i)
# Print vertices belongs to both sets
for i in range(2):
for j in range(len(dis[i])):
print(dis[i][j], end = " ")
print('\n', end = "")
# Driver code
if __name__ == '__main__':
n = 6
m = 4
# Add edges
Add_edge(1, 2)
Add_edge(2, 3)
Add_edge(2, 4)
Add_edge(5, 6)
# Function call
goodsets(n)
# This code is contributed
# by Surendra_Gangwar
C#
// C# program to find two
// disjoint good sets of
// vertices in a given graph
using System;
using System.Collections.Generic;
class GFG{
static int N = 100005;
// For the graph
static List<int>[] gr =
new List<int>[N],
dis = new List<int>[2];
static bool[] vis = new bool[N];
static int[] color = new int[N];
static bool bip;
// Function to add edge
static void add_edge(int x,
int y)
{
gr[x].Add(y);
gr[y].Add(x);
}
// Bipartite function
static void dfs(int x,
int col)
{
vis[x] = true;
color[x] = col;
// Check for child vertices
foreach (int i in gr[x])
{
// If it is not visited
if (!vis[i])
dfs(i, col ^ 1);
// If it is already visited
else if (color[i] == col)
bip = false;
}
}
// Function to find two disjoint
// good sets of vertices in a
// given graph
static void goodsets(int n)
{
// Initially assume that
// graph is bipartite
bip = true;
// For every unvisited
// vertex call dfs
for (int i = 1; i <= n; i++)
if (!vis[i])
dfs(i, 0);
// If graph is not bipartite
if (!bip)
Console.WriteLine(-1);
else
{
// Differentiate two sets
for (int i = 1;
i <= n; i++)
dis[color[i]].Add(i);
// Print vertices belongs
// to both sets
for (int i = 0; i < 2; i++)
{
for (int j = 0;
j < dis[i].Count; j++)
Console.Write(dis[i][j] + " ");
Console.WriteLine();
}
}
}
// Driver Code
public static void Main(String[] args)
{
int n = 6, m = 4;
for (int i = 0; i < N; i++)
gr[i] = new List<int>();
for (int i = 0; i < 2; i++)
dis[i] = new List<int>();
// Add edges
add_edge(1, 2);
add_edge(2, 3);
add_edge(2, 4);
add_edge(5, 6);
// Function call
goodsets(n);
}
}
// This code is contributed by shikhasingrajput
Javascript
<script>
// JavaScript program to find two
// disjoint good sets of
// vertices in a given graph
var N = 100005;
// For the graph
var gr = Array.from(Array(N), ()=>Array());
var dis = Array.from(Array(2), ()=>Array());
var vis = Array(N).fill(false);
var color = Array(N).fill(0);
var bip;
// Function to add edge
function add_edge(x, y)
{
gr[x].push(y);
gr[y].push(x);
}
// Bipartite function
function dfs(x, col)
{
vis[x] = true;
color[x] = col;
// Check for child vertices
for(var i of gr[x])
{
// If it is not visited
if (!vis[i])
dfs(i, col ^ 1);
// If it is already visited
else if (color[i] == col)
bip = false;
}
}
// Function to find two disjoint
// good sets of vertices in a
// given graph
function goodsets(n)
{
// Initially assume that
// graph is bipartite
bip = true;
// For every unvisited
// vertex call dfs
for (var i = 1; i <= n; i++)
if (!vis[i])
dfs(i, 0);
// If graph is not bipartite
if (!bip)
document.write(-1 + "<br>");
else
{
// Differentiate two sets
for (var i = 1;
i <= n; i++)
dis[color[i]].push(i);
// Print vertices belongs
// to both sets
for (var i = 0; i < 2; i++)
{
for (var j = 0;
j < dis[i].length; j++)
document.write(dis[i][j] + " ");
document.write("<br>")
}
}
}
// Driver Code
var n = 6, m = 4;
// push edges
add_edge(1, 2);
add_edge(2, 3);
add_edge(2, 4);
add_edge(5, 6);
// Function call
goodsets(n);
</script>
1 3 4 5 2 6
Complejidad de tiempo: O(n)
Complejidad espacial: O(n)
Publicación traducida automáticamente
Artículo escrito por pawan_asipu y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA