Dada una array arr[] de tamaño N que tiene números enteros en el rango [1, N] y faltan algunos de los elementos. La tarea es encontrar los elementos que faltan.
Nota: Puede haber duplicados en la array.
Ejemplos:
Entrada: arr[] = {1, 3, 3, 3, 5}, N = 5
Salida: 2 4
Explicación: Los números que faltan en la lista son 2 y 4
Todos los demás elementos en el rango [1, 5] están presentes en la array.Entrada: arr[] = {1, 2, 3, 4, 4, 7, 7}, N = 7
Salida: 5 6
Enfoque 1 (Negación de elementos visitados): La idea para resolver el problema es la siguiente
En el rango dado [1, N] debe haber un elemento correspondiente a cada índice. Entonces marque los índices visitados multiplicando ese elemento con -1 . Si falta un elemento, su índice tendrá un elemento positivo. De lo contrario, tendrá un elemento negativo.
Siga la siguiente ilustración:
Ilustración:
Considere arr[] = {1, 3, ,3, 3, 5}
Aquí, como ilustración, usaremos la indexación basada en 1Para i = 1:
=> arr[i] = 1. Entonces marque arr[1] visitado.
=> array[1] = -1*array[1] = -1*1 = -1
=> array[] = {-1, 3, 3, 3, 5}Para i = 2:
=> arr[i] = 3. Entonces marque arr[3] visitado.
=> array[3] = -1*array[3] = -1*3 = -3
=> array[] = {-1, 3, -3, 3, 5}Para i = 3:
=> arr[i] = -3. Así que deberíamos pasar al valor absoluto de -3, es decir, 3
=> arr[3] ya está visitado. Saltar al índice siguiente
=> arr[] = {-1, 3, -3, 3, 5}Para i = 4:
=> arr[i] = 3. Entonces marque arr[3] visitado.
=> arr[3] ya fue visitado. Saltar al índice siguiente
=> arr[] = {-1, 3, -3, 3, 5}Para i = 5:
=> arr[i] = 5. Entonces marque arr[5] visitado.
=> array[5] = -1*array[5] = -1*5 = -5
=> array[] = {-1, 3, -3, 3, -5}De nuevo atraviesa la array. Vea que arr[2] y arr[4] no se visiten.
Entonces los elementos que faltan son {2, 4} .
Siga los siguientes pasos para implementar la idea:
- Recorra la array desde i = 0 hasta N-1:
- Si el elemento es negativo, tome el valor positivo (digamos x = abs(arr[i]) ).
- si el valor en (x-1) el índice no se visita, es decir, todavía es positivo, entonces multiplique ese elemento con -1 .
- Atraviese la array nuevamente desde i = 0 a N-1 :
- Si el elemento no se visita, es decir, tiene un valor positivo, empuje (i+1) a la array resultante.
- Devuelve la array resultante que contiene los elementos que faltan.
A continuación se muestra la implementación del enfoque anterior:
C++
// C++ implementation of the approach
#include <bits/stdc++.h>
using namespace std;
// Function to find the missing elements
vector<int> missing_elements(vector<int> vec)
{
// Vector to store the list
// of missing elements
vector<int> mis;
// For every given element
for (int i = 0; i < vec.size(); i++) {
// Find its index
int temp = abs(vec[i]) - 1;
// Update the element at the found index
vec[temp] = vec[temp] > 0
? -vec[temp] : vec[temp];
}
for (int i = 0; i < vec.size(); i++)
// Current element was not present
// in the original vector
if (vec[i] > 0)
mis.push_back(i + 1);
return mis;
}
// Driver code
int main()
{
vector<int> vec = { 3, 3, 3, 5, 1 };
// Vector to store the returned
// list of missing elements
vector<int> miss_ele = missing_elements(vec);
// Print the list of elements
for (int i = 0; i < miss_ele.size(); i++)
cout << miss_ele[i] << " ";
return 0;
}
// This code is contributed by Aditya Kumar (adityakumar129)
C
// C implementation of the approach
#include <stdio.h>
#include <stdlib.h>
// Function to find the missing elements
void missing_elements(int vec[], int n)
{
int mis[n];
for (int i = 0; i < n; i++)
mis[i] = -1;
// For every given element
for (int i = 0; i < n; i++) {
// Find its index
int temp = abs(vec[i]) - 1;
// Update the element at the found index
vec[temp] = vec[temp] > 0 ? -vec[temp] : vec[temp];
}
// Current element was not present
// in the original vector
for (int i = 0; i < n; i++)
if (vec[i] > 0)
mis[i] = (i + 1);
int miss_ele_size = sizeof(mis) / sizeof(mis[0]);
for (int i = 0; i < miss_ele_size; i++) {
if (mis[i] != -1)
printf("%d ", mis[i]);
}
}
// Driver code
int main()
{
int vec[] = { 3, 3, 3, 5, 1 };
int vec_size = sizeof(vec) / sizeof(vec[0]);
missing_elements(vec, vec_size);
return 0;
}
// This code is contributed by Aditya Kumar (adityakumar129)
Java
// Java implementation of the above approach
import java.util.*;
class GFG {
// Function to find the missing elements
static List<Integer>
missing_elements(List<Integer> vec)
{
// Vector to store the list
// of missing elements
List<Integer> mis = new ArrayList<Integer>();
// For every given element
for (int i = 0; i < vec.size(); i++) {
// Find its index
int temp = Math.abs((int)vec.get(i)) - 1;
// Update the element at the found index
if ((int)vec.get(temp) > 0)
vec.set(temp, -(int)vec.get(temp));
else
vec.set(temp, vec.get(temp));
}
for (int i = 0; i < vec.size(); i++) {
// Current element was not present
// in the original vector
if ((int)vec.get(i) > 0)
mis.add(i + 1);
}
return mis;
}
// Driver code
public static void main(String args[])
{
List<Integer> vec = new ArrayList<Integer>();
vec.add(3);
vec.add(3);
vec.add(3);
vec.add(5);
vec.add(1);
// Vector to store the returned
// list of missing elements
List<Integer> miss_ele = missing_elements(vec);
// Print the list of elements
for (int i = 0; i < miss_ele.size(); i++)
System.out.print(miss_ele.get(i) + " ");
}
}
// This code is contributed by Aditya Kumar (adityakumar129)
Python3
# Python3 implementation of the approach # Function to find the missing elements def missing_elements(vec): # Vector to store the list # of missing elements mis = [] # For every given element for i in range(len(vec)): # Find its index temp = abs(vec[i]) - 1 # Update the element at the found index if vec[temp] > 0: vec[temp] = -vec[temp] for i in range(len(vec)): # Current element was not present # in the original vector if (vec[i] > 0): mis.append(i + 1) return mis # Driver code if __name__ == '__main__': vec = [3, 3, 3, 5, 1] # Vector to store the returned # list of missing elements miss_ele = missing_elements(vec) # Print the list of elements for i in range(len(miss_ele)): print(miss_ele[i], end=" ") # This code is contributed by Mohit Kumar
C#
// C# implementation of the approach
using System;
using System.Collections.Generic;
class GFG {
// Function to find the missing elements
static List<int> missing_elements(List<int> vec)
{
// List<int> to store the list
// of missing elements
List<int> mis = new List<int>();
// For every given element
for (int i = 0; i < vec.Count; i++) {
// Find its index
int temp = Math.Abs((int)vec[i]) - 1;
// Update the element at the found index
if ((int)vec[temp] > 0)
vec[temp] = -(int)vec[temp];
else
vec[temp] = vec[temp];
}
for (int i = 0; i < vec.Count; i++) {
// Current element was not present
// in the original vector
if ((int)vec[i] > 0)
mis.Add(i + 1);
}
return mis;
}
// Driver code
public static void Main(String[] args)
{
List<int> vec = new List<int>();
vec.Add(3);
vec.Add(3);
vec.Add(3);
vec.Add(5);
vec.Add(1);
// List to store the returned
// list of missing elements
List<int> miss_ele = missing_elements(vec);
// Print the list of elements
for (int i = 0; i < miss_ele.Count; i++)
Console.Write(miss_ele[i] + " ");
}
}
// This code is contributed by 29AjayKumar
Javascript
<script>
// Javascript implementation of the approach
// Function to find the missing elements
function missing_elements(vec)
{
// Vector to store the list
// of missing elements
let mis = [];
// For every given element
for (let i = 0; i < vec.length; i++) {
// Find its index
let temp = Math.abs(vec[i]) - 1;
// Update the element at the found index
vec[temp] = vec[temp] > 0 ? -vec[temp] : vec[temp];
}
for (let i = 0; i < vec.length; i++)
// Current element was not present
// in the original vector
if (vec[i] > 0)
mis.push(i + 1);
return mis;
}
let vec = [ 3, 3, 3, 5, 1 ];
// Vector to store the returned
// list of missing elements
let miss_ele = missing_elements(vec);
// Print the list of elements
for (let i = 0; i < miss_ele.length; i++)
document.write(miss_ele[i] + " ");
</script>
2 4
Complejidad temporal: O(N).
Espacio Auxiliar: O(N)
Enfoque 2 (Realización de clasificación en el lugar): La idea en este caso es utilizar la clasificación en el lugar.
En el rango dado [1, N] debe haber un elemento correspondiente a cada índice. Entonces podemos ordenarlos y luego, si en cualquier índice, la posición y el elemento no son los mismos, esos elementos faltan.
Para ordenar los elementos en tiempo lineal, consulte el siguiente pseudocódigo:
Pseudocódigo:
Algoritmo:
Start
Set pointer i = 0
while i < N:
pos = arr[i] – 1
If arr[pos] = pos + 1: // el elemento está en la posición correcta
i++
Else: // cambiarlo a la posición correcta
swap(arr[pos], arr[i])
end if
end while
for i = 0 to N-1:
If Arr[i] = i+1:
continue
Else:
falta i+1.
fin si
fin para
Fin
Siga la ilustración a continuación para una mejor comprensión:
Ilustración:
Considere arr[] = {3, 3, 3, 5, 1}
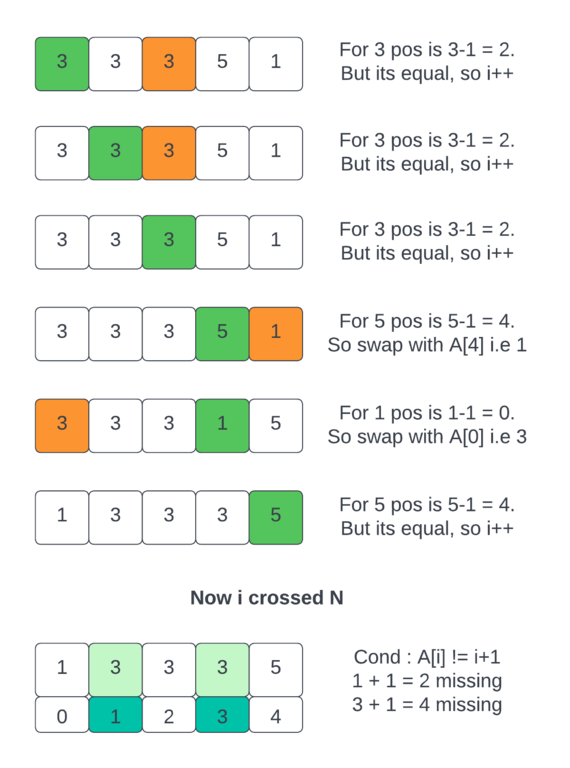
Ejemplo de cómo ordenar en ordenación lineal
A continuación se muestra la implementación del enfoque anterior:
C++
// C++ code ot implement the approach
#include <bits/stdc++.h>
using namespace std;
// Function to find the missing elements
vector<int> FindMissing(vector<int> arr)
{
int i = 0;
int N = arr.size();
while (i < N) {
// as 0 based indxing
int correct = arr[i] - 1;
if (arr[i] != arr[correct]) {
swap(arr[i], arr[correct]);
}
else {
i++;
}
}
vector<int> ans;
for (i = 0; i < N; i++) {
if (arr[i] != i + 1) {
ans.push_back(i + 1);
}
}
return ans;
}
// Driver code
int main()
{
vector<int> arr = { 1, 3, 3, 3, 5 };
// Function call
vector<int> res = FindMissing(arr);
for(int x: res)
cout << x << " ";
return 0;
}
// Code done by R.Balakrishnan (rbkraj000)
2 4
Complejidad de tiempo: O(N)
Incluso en el peor de los casos, se realizarán N-1 intercambios + N-1 comparaciones. Entonces asintóticamente es O(N).
Espacio Auxiliar: O(N)
Publicación traducida automáticamente
Artículo escrito por isa_aanchal y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA