Dada una cuadrícula de números, encuentre la secuencia de serpiente de longitud máxima e imprímala. Si existen varias secuencias de serpientes con la longitud máxima, imprima cualquiera de ellas.
Una secuencia de serpientes se compone de números adyacentes en la cuadrícula, de modo que para cada número, el número de la derecha o el número de abajo es +1 o -1 su valor. Por ejemplo, si se encuentra en la ubicación (x, y) de la cuadrícula, puede moverse hacia la derecha, es decir, (x, y+1) si ese número es ± 1, o puede moverse hacia abajo, es decir, (x+1, y) si ese número es ± 1.
For example, 9, 6, 5, 2 8, 7, 6, 5 7, 3, 1, 6 1, 1, 1, 7 In above grid, the longest snake sequence is: (9, 8, 7, 6, 5, 6, 7)
La siguiente figura muestra todos los caminos posibles:
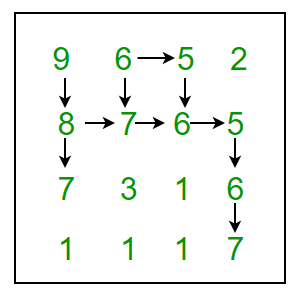
Le recomendamos encarecidamente que minimice su navegador y que pruebe esto usted mismo primero.
La idea es usar Programación Dinámica. Para cada celda de la array, mantenemos la longitud máxima de una serpiente que termina en la celda actual. La secuencia de serpiente de longitud máxima tendrá el valor máximo. La celda de valor máximo corresponderá a la cola de la serpiente. Para imprimir la serpiente, necesitamos retroceder desde la cola hasta la cabeza de la serpiente.
Let T[i][i] represent maximum length of a snake which ends at cell (i, j), then for given matrix M, the DP relation is defined as T[0][0] = 0 T[i][j] = max(T[i][j], T[i][j - 1] + 1) if M[i][j] = M[i][j - 1] ± 1 T[i][j] = max(T[i][j], T[i - 1][j] + 1) if M[i][j] = M[i - 1][j] ± 1
A continuación se muestra la implementación de la idea.
C++
// C++ program to find maximum length
// Snake sequence and print it
#include <bits/stdc++.h>
using namespace std;
#define M 4
#define N 4
struct Point
{
int x, y;
};
// Function to find maximum length Snake sequence path
// (i, j) corresponds to tail of the snake
list<Point> findPath(int grid[M][N], int mat[M][N],
int i, int j)
{
list<Point> path;
Point pt = {i, j};
path.push_front(pt);
while (grid[i][j] != 0)
{
if (i > 0 &&
grid[i][j] - 1 == grid[i - 1][j])
{
pt = {i - 1, j};
path.push_front(pt);
i--;
}
else if (j > 0 &&
grid[i][j] - 1 == grid[i][j - 1])
{
pt = {i, j - 1};
path.push_front(pt);
j--;
}
}
return path;
}
// Function to find maximum length Snake sequence
void findSnakeSequence(int mat[M][N])
{
// table to store results of subproblems
int lookup[M][N];
// initialize by 0
memset(lookup, 0, sizeof lookup);
// stores maximum length of Snake sequence
int max_len = 0;
// store coordinates to snake's tail
int max_row = 0;
int max_col = 0;
// fill the table in bottom-up fashion
for (int i = 0; i < M; i++)
{
for (int j = 0; j < N; j++)
{
// do except for (0, 0) cell
if (i || j)
{
// look above
if (i > 0 &&
abs(mat[i - 1][j] - mat[i][j]) == 1)
{
lookup[i][j] = max(lookup[i][j],
lookup[i - 1][j] + 1);
if (max_len < lookup[i][j])
{
max_len = lookup[i][j];
max_row = i, max_col = j;
}
}
// look left
if (j > 0 &&
abs(mat[i][j - 1] - mat[i][j]) == 1)
{
lookup[i][j] = max(lookup[i][j],
lookup[i][j - 1] + 1);
if (max_len < lookup[i][j])
{
max_len = lookup[i][j];
max_row = i, max_col = j;
}
}
}
}
}
cout << "Maximum length of Snake sequence is: "
<< max_len << endl;
// find maximum length Snake sequence path
list<Point> path = findPath(lookup, mat, max_row,
max_col);
cout << "Snake sequence is:";
for (auto it = path.begin(); it != path.end(); it++)
cout << endl << mat[it->x][it->y] << " ("
<< it->x << ", " << it->y << ")" ;
}
// Driver code
int main()
{
int mat[M][N] =
{
{9, 6, 5, 2},
{8, 7, 6, 5},
{7, 3, 1, 6},
{1, 1, 1, 7},
};
findSnakeSequence(mat);
return 0;
}
Java
// Java program to find maximum length
// Snake sequence and print it
import java.util.*;
class GFG
{
static int M = 4;
static int N = 4;
static class Point
{
int x, y;
public Point(int x, int y)
{
this.x = x;
this.y = y;
}
};
// Function to find maximum length Snake sequence path
// (i, j) corresponds to tail of the snake
static List<Point> findPath(int grid[][],
int mat[][],
int i, int j)
{
List<Point> path = new LinkedList<>();
Point pt = new Point(i, j);
path.add(0, pt);
while (grid[i][j] != 0)
{
if (i > 0 &&
grid[i][j] - 1 == grid[i - 1][j])
{
pt = new Point(i - 1, j);
path.add(0, pt);
i--;
}
else if (j > 0 && grid[i][j] - 1 ==
grid[i][j - 1])
{
pt = new Point(i, j - 1);
path.add(0, pt);
j--;
}
}
return path;
}
// Function to find maximum length Snake sequence
static void findSnakeSequence(int mat[][])
{
// table to store results of subproblems
int [][]lookup = new int[M][N];
// initialize by 0
// stores maximum length of Snake sequence
int max_len = 0;
// store coordinates to snake's tail
int max_row = 0;
int max_col = 0;
// fill the table in bottom-up fashion
for (int i = 0; i < M; i++)
{
for (int j = 0; j < N; j++)
{
// do except for (0, 0) cell
if (i != 0 || j != 0)
{
// look above
if (i > 0 &&
Math.abs(mat[i - 1][j] -
mat[i][j]) == 1)
{
lookup[i][j] = Math.max(lookup[i][j],
lookup[i - 1][j] + 1);
if (max_len < lookup[i][j])
{
max_len = lookup[i][j];
max_row = i; max_col = j;
}
}
// look left
if (j > 0 &&
Math.abs(mat[i][j - 1] -
mat[i][j]) == 1)
{
lookup[i][j] = Math.max(lookup[i][j],
lookup[i][j - 1] + 1);
if (max_len < lookup[i][j])
{
max_len = lookup[i][j];
max_row = i; max_col = j;
}
}
}
}
}
System.out.print("Maximum length of Snake " +
"sequence is: " + max_len + "\n");
// find maximum length Snake sequence path
List<Point> path = findPath(lookup, mat, max_row,
max_col);
System.out.print("Snake sequence is:");
for (Point it : path)
System.out.print("\n" + mat[it.x][it.y] + " (" +
it.x + ", " + it.y + ")");
}
// Driver code
public static void main(String[] args)
{
int mat[][] = {{9, 6, 5, 2},
{8, 7, 6, 5},
{7, 3, 1, 6},
{1, 1, 1, 7}};
findSnakeSequence(mat);
}
}
// This code is contributed by 29AjayKumar
C#
// C# program to find maximum length
// Snake sequence and print it
using System;
using System.Collections.Generic;
class GFG {
static int M = 4;
static int N = 4;
public class Point {
public int x, y;
public Point(int x, int y)
{
this.x = x;
this.y = y;
}
};
// Function to find maximum length Snake sequence path
// (i, j) corresponds to tail of the snake
static List<Point> findPath(int[, ] grid, int[, ] mat,
int i, int j)
{
List<Point> path = new List<Point>();
Point pt = new Point(i, j);
path.Insert(0, pt);
while (grid[i, j] != 0) {
if (i > 0 && grid[i, j] - 1 == grid[i - 1, j]) {
pt = new Point(i - 1, j);
path.Insert(0, pt);
i--;
}
else if (j > 0
&& grid[i, j] - 1 == grid[i, j - 1]) {
pt = new Point(i, j - 1);
path.Insert(0, pt);
j--;
}
}
return path;
}
// Function to find maximum length Snake sequence
static void findSnakeSequence(int[, ] mat)
{
// table to store results of subproblems
int[, ] lookup = new int[M, N];
// initialize by 0
// stores maximum length of Snake sequence
int max_len = 0;
// store coordinates to snake's tail
int max_row = 0;
int max_col = 0;
// fill the table in bottom-up fashion
for (int i = 0; i < M; i++) {
for (int j = 0; j < N; j++) {
// do except for (0, 0) cell
if (i != 0 || j != 0) {
// look above
if (i > 0
&& Math.Abs(mat[i - 1, j]
- mat[i, j])
== 1) {
lookup[i, j] = Math.Max(
lookup[i, j],
lookup[i - 1, j] + 1);
if (max_len < lookup[i, j]) {
max_len = lookup[i, j];
max_row = i;
max_col = j;
}
}
// look left
if (j > 0
&& Math.Abs(mat[i, j - 1]
- mat[i, j])
== 1) {
lookup[i, j] = Math.Max(
lookup[i, j],
lookup[i, j - 1] + 1);
if (max_len < lookup[i, j]) {
max_len = lookup[i, j];
max_row = i;
max_col = j;
}
}
}
}
}
Console.Write("Maximum length of Snake "
+ "sequence is: " + max_len + "\n");
// find maximum length Snake sequence path
List<Point> path
= findPath(lookup, mat, max_row, max_col);
Console.Write("Snake sequence is:");
foreach(Point it in path)
Console.Write("\n" + mat[it.x, it.y] + " ("
+ it.x + ", " + it.y + ")");
}
// Driver code
public static void Main(String[] args)
{
int[, ] mat = { { 9, 6, 5, 2 },
{ 8, 7, 6, 5 },
{ 7, 3, 1, 6 },
{ 1, 1, 1, 7 } };
findSnakeSequence(mat);
}
}
// This code is contributed by Princi Singh
Python3
def snakesequence(S, m, n):
sequence = {}
DP = [[1 for x in range(m+1)] for x in range(n+1)]
a, b, maximum = 0, 0, 0
position = [0, 0]
for i in range(0, n+1):
for j in range(0, m+1):
a, b = 0, 0
p = "initial"
if(i > 0 and abs(S[i][j] - S[i-1][j]) == 1):
a = DP[i-1][j]
if(j > 0 and abs(S[i][j] - S[i][j-1]) == 1):
b = DP[i][j-1]
if a != 0 and a >= b:
p = str(i-1) + " " + str(j)
elif b != 0:
p = str(i) + " " + str(j-1)
q = str(i) + " " + str(j)
sequence[q] = p
DP[i][j] = DP[i][j] + max(a, b)
if DP[i][j] >= maximum:
maximum = DP[i][j]
position[0] = i
position[1] = j
snakeValues = []
snakePositions = []
snakeValues.append(S[position[0]][position[1]])
check = 'found'
str_next = str(position[0]) + " " + str(position[1])
findingIndices = sequence[str_next].split()
while(check == 'found'):
if sequence[str_next] == 'initial':
snakePositions.insert(0, str_next)
check = 'end'
continue
findingIndices = sequence[str_next].split()
g = int(findingIndices[0])
h = int(findingIndices[1])
snakeValues.insert(0, S[g][h])
snake_position = str(g) + " " + str(h)
snakePositions.insert(0, str_next)
str_next = sequence[str_next]
return [snakeValues, snakePositions]
S = [[9, 6, 5, 2],
[8, 7, 6, 5],
[7, 3, 1, 6],
[1, 1, 10, 7]]
m = 3
n = 3
seq = snakesequence(S, m, n)
for i in range(len(seq[0])):
print(seq[0][i], ",", seq[1][i].split())
Maximum length of Snake sequence is: 6 Snake sequence is: 9 (0, 0) 8 (1, 0) 7 (1, 1) 6 (1, 2) 5 (1, 3) 6 (2, 3) 7 (3, 3)
La complejidad temporal de la solución anterior es O(M*N). El espacio auxiliar utilizado por la solución anterior es O(M*N). Si no estamos obligados a imprimir la serpiente, el espacio se puede reducir aún más a O (N) ya que solo usamos el resultado de la última fila.
Este artículo es una contribución de Aditya Goel . Si le gusta GeeksforGeeks y le gustaría contribuir, también puede escribir un artículo y enviarlo por correo a review-team@geeksforgeeks.org. Vea su artículo que aparece en la página principal de GeeksforGeeks y ayude a otros Geeks.
Publicación traducida automáticamente
Artículo escrito por GeeksforGeeks-1 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA