Dada la raíz de un árbol de búsqueda binario y K como entrada, encuentre el K-ésimo elemento más pequeño en BST.
Por ejemplo, en el siguiente BST, si k = 3, la salida debería ser 10, y si k = 5, la salida debería ser 14.
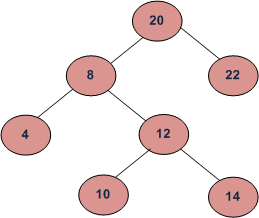
Método 1: Usando Inorder Traversal (tiempo O(n) y espacio auxiliar O(h))
El recorrido en orden de un BST atraviesa los Nodes en orden creciente. Así que la idea es atravesar el árbol en orden. Mientras atraviesa, realice un seguimiento del recuento de los Nodes visitados. Si el conteo se convierte en k, imprima el Node.
C++
// A simple inorder traversal based C++ program to find k-th
// smallest element in a BST.
#include <iostream>
using namespace std;
// A BST node
struct Node {
int data;
Node *left, *right;
Node(int x)
{
data = x;
left = right = NULL;
}
};
// Recursive function to insert an key into BST
Node* insert(Node* root, int x)
{
if (root == NULL)
return new Node(x);
if (x < root->data)
root->left = insert(root->left, x);
else if (x > root->data)
root->right = insert(root->right, x);
return root;
}
// Function to find k'th smallest element in BST
// Here count denotes the number of nodes processed so far
int count = 0;
Node* kthSmallest(Node* root, int& k)
{
// base case
if (root == NULL)
return NULL;
// search in left subtree
Node* left = kthSmallest(root->left, k);
// if k'th smallest is found in left subtree, return it
if (left != NULL)
return left;
// if current element is k'th smallest, return it
count++;
if (count == k)
return root;
// else search in right subtree
return kthSmallest(root->right, k);
}
// Function to print k'th smallest element in BST
void printKthSmallest(Node* root, int k)
{
// maintain index to count number of nodes processed so far
Node* res = kthSmallest(root, k);
if (res == NULL)
cout << "There are less than k nodes in the BST";
else
cout << "K-th Smallest Element is " << res->data;
}
// main function
int main()
{
Node* root = NULL;
int keys[] = { 20, 8, 22, 4, 12, 10, 14 };
for (int x : keys)
root = insert(root, x);
int k = 3;
printKthSmallest(root, k);
return 0;
}
// This code is contributed by Aditya Kumar (adityakumar129)
C
// A simple inorder traversal based C++ program to find k-th
// smallest element in a BST.
#include <stdio.h>
#include <stdlib.h>
// A BST node
typedef struct Node {
int data;
struct Node *left, *right;
} Node;
struct Node* new_node(int x)
{
struct Node* p = malloc(sizeof(struct Node));
p->data = x;
p->left = NULL;
p->right = NULL;
return p;
}
// Recursive function to insert an key into BST
Node* insert(Node* root, int x)
{
if (root == NULL)
return new_node(x);
if (x < root->data)
root->left = insert(root->left, x);
else if (x > root->data)
root->right = insert(root->right, x);
return root;
}
// Function to find k'th smallest element in BST
// Here count denotes the number of nodes processed so far
int count = 0;
Node* kthSmallest(Node* root, int k)
{
// base case
if (root == NULL)
return NULL;
// search in left subtree
Node* left = kthSmallest(root->left, k);
// if k'th smallest is found in left subtree, return it
if (left != NULL)
return left;
// if current element is k'th smallest, return it
count++;
if (count == k)
return root;
// else search in right subtree
return kthSmallest(root->right, k);
}
// Function to print k'th smallest element in BST
void printKthSmallest(Node* root, int k)
{
// maintain index to count number of nodes processed so far
Node* res = kthSmallest(root, k);
if (res == NULL)
printf("There are less than k nodes in the BST");
else
printf("K-th Smallest Element is %d", res->data);
}
// main function
int main()
{
Node* root = NULL;
int keys[] = { 20, 8, 22, 4, 12, 10, 14 };
int keys_size = sizeof(keys) / sizeof(keys[0]);
for (int i = 0; i < keys_size; i++)
root = insert(root, keys[i]);
int k = 3;
printKthSmallest(root, k);
return 0;
}
// This code is contributed by Aditya Kumar (adityakumar129)
Java
// A simple inorder traversal based Java program
// to find k-th smallest element in a BST.
import java.io.*;
// A BST node
class Node {
int data;
Node left, right;
Node(int x)
{
data = x;
left = right = null;
}
}
class GFG {
static int count = 0;
// Recursive function to insert an key into BST
public static Node insert(Node root, int x)
{
if (root == null)
return new Node(x);
if (x < root.data)
root.left = insert(root.left, x);
else if (x > root.data)
root.right = insert(root.right, x);
return root;
}
// Function to find k'th largest element in BST
// Here count denotes the number of nodes processed so far
public static Node kthSmallest(Node root, int k)
{
// base case
if (root == null)
return null;
// search in left subtree
Node left = kthSmallest(root.left, k);
// if k'th smallest is found in left subtree, return it
if (left != null)
return left;
// if current element is k'th smallest, return it
count++;
if (count == k)
return root;
// else search in right subtree
return kthSmallest(root.right, k);
}
// Function to find k'th largest element in BST
public static void printKthSmallest(Node root, int k)
{
Node res = kthSmallest(root, k);
if (res == null)
System.out.println("There are less than k nodes in the BST");
else
System.out.println("K-th Smallest Element is " + res.data);
}
public static void main(String[] args)
{
Node root = null;
int keys[] = { 20, 8, 22, 4, 12, 10, 14 };
for (int x : keys)
root = insert(root, x);
int k = 3;
printKthSmallest(root, k);
}
}
// This code is contributed by Aditya Kumar (adityakumar129)
Python3
# A simple inorder traversal based Python3
# program to find k-th smallest element
# in a BST.
# A BST node
class Node:
def __init__(self, key):
self.data = key
self.left = None
self.right = None
# Recursive function to insert an key into BST
def insert(root, x):
if (root == None):
return Node(x)
if (x < root.data):
root.left = insert(root.left, x)
elif (x > root.data):
root.right = insert(root.right, x)
return root
# Function to find k'th largest element
# in BST. Here count denotes the number
# of nodes processed so far
def kthSmallest(root):
global k
# Base case
if (root == None):
return None
# Search in left subtree
left = kthSmallest(root.left)
# If k'th smallest is found in
# left subtree, return it
if (left != None):
return left
# If current element is k'th
# smallest, return it
k -= 1
if (k == 0):
return root
# Else search in right subtree
return kthSmallest(root.right)
# Function to find k'th largest element in BST
def printKthSmallest(root):
# Maintain index to count number
# of nodes processed so far
count = 0
res = kthSmallest(root)
if (res == None):
print("There are less than k nodes in the BST")
else:
print("K-th Smallest Element is ", res.data)
# Driver code
if __name__ == '__main__':
root = None
keys = [ 20, 8, 22, 4, 12, 10, 14 ]
for x in keys:
root = insert(root, x)
k = 3
printKthSmallest(root)
# This code is contributed by mohit kumar 29
C#
// A simple inorder traversal
// based C# program to find
// k-th smallest element in a BST.
using System;
// A BST node
class Node{
public int data;
public Node left, right;
public Node(int x)
{
data = x;
left = right = null;
}
}
class GFG{
static int count = 0;
// Recursive function to
// insert an key into BST
public static Node insert(Node root,
int x)
{
if (root == null)
return new Node(x);
if (x < root.data)
root.left = insert(root.left, x);
else if (x > root.data)
root.right = insert(root.right, x);
return root;
}
// Function to find k'th largest
// element in BST. Here count
// denotes the number of nodes
// processed so far
public static Node kthSmallest(Node root,
int k)
{
// base case
if (root == null)
return null;
// search in left subtree
Node left = kthSmallest(root.left, k);
// if k'th smallest is found
// in left subtree, return it
if (left != null)
return left;
// if current element is
// k'th smallest, return it
count++;
if (count == k)
return root;
// else search in right subtree
return kthSmallest(root.right, k);
}
// Function to find k'th largest
// element in BST
public static void printKthSmallest(Node root,
int k)
{
// Maintain an index to
// count number of nodes
// processed so far
count = 0;
Node res = kthSmallest(root, k);
if (res == null)
Console.WriteLine("There are less " +
"than k nodes in the BST");
else
Console.WriteLine("K-th Smallest" +
" Element is " + res.data);
}
// Driver code
public static void Main(String[] args)
{
Node root = null;
int []keys = {20, 8, 22, 4,
12, 10, 14};
foreach (int x in keys)
root = insert(root, x);
int k = 3;
printKthSmallest(root, k);
}
}
// This code is contributed by gauravrajput1
Javascript
<script>
// A simple inorder traversal based Javascript program
// to find k-th smallest element in a BST.
// A BST node
class Node
{
constructor(x) {
this.data = x;
this.left = null;
this.right = null;
}
}
let count = 0;
// Recursive function to insert an key into BST
function insert(root,x)
{
if (root == null)
return new Node(x);
if (x < root.data)
root.left = insert(root.left, x);
else if (x > root.data)
root.right = insert(root.right, x);
return root;
}
// Function to find k'th largest element in BST
// Here count denotes the number
// of nodes processed so far
function kthSmallest(root,k)
{
// base case
if (root == null)
return null;
// search in left subtree
let left = kthSmallest(root.left, k);
// if k'th smallest is found in left subtree, return it
if (left != null)
return left;
// if current element is k'th smallest, return it
count++;
if (count == k)
return root;
// else search in right subtree
return kthSmallest(root.right, k);
}
// Function to find k'th largest element in BST
function printKthSmallest(root,k)
{
// maintain an index to count number of
// nodes processed so far
count = 0;
let res = kthSmallest(root, k);
if (res == null)
document.write("There are less "
+ "than k nodes in the BST");
else
document.write("K-th Smallest"
+ " Element is " + res.data);
}
let root=null;
let key=[20, 8, 22, 4, 12, 10, 14 ];
for(let i=0;i<key.length;i++)
{
root = insert(root, key[i]);
}
let k = 3;
printKthSmallest(root, k);
// This code is contributed by unknown2108
</script>
K-th Smallest Element is 10
Podemos optimizar el espacio utilizando Morris Traversal . Consulte el elemento más pequeño K’th en BST usando O (1) Extra Space para obtener más detalles.
Método 2: Estructura de datos de árbol aumentado (O(h) Complejidad de tiempo y O(h) espacio auxiliar)
La idea es mantener el rango de cada Node. Podemos realizar un seguimiento de los elementos en el subárbol izquierdo de cada Node mientras construimos el árbol. Como necesitamos el K-ésimo elemento más pequeño, podemos mantener el número de elementos del subárbol izquierdo en cada Node.
Suponga que la raíz tiene Nodes ‘lCount’ en su subárbol izquierdo. Si K = lCount + 1, la raíz es el K-ésimo Node. Si K < lCuenta + 1, continuaremos nuestra búsqueda (recursión) del K-ésimo elemento más pequeño en el subárbol izquierdo de la raíz. Si K > lCount + 1, continuamos nuestra búsqueda en el subárbol derecho del (K – lCount – 1)-ésimo elemento más pequeño. Tenga en cuenta que solo necesitamos el recuento de elementos en el subárbol izquierdo.
C++
// A simple inorder traversal based C++ program to find k-th
// smallest element in a BST.
#include <iostream>
using namespace std;
// A BST node
struct Node {
int data;
Node *left, *right;
int lCount;
Node(int x)
{
data = x;
left = right = NULL;
lCount = 0;
}
};
// Recursive function to insert an key into BST
Node* insert(Node* root, int x)
{
if (root == NULL)
return new Node(x);
// If a node is inserted in left subtree, then lCount of
// this node is increased. For simplicity, we are
// assuming that all keys (tried to be inserted) are
// distinct.
if (x < root->data) {
root->left = insert(root->left, x);
root->lCount++;
}
else if (x > root->data)
root->right = insert(root->right, x);
return root;
}
// Function to find k'th smallest element in BST
// Here count denotes the number of nodes processed so far
Node* kthSmallest(Node* root, int k)
{
// base case
if (root == NULL)
return NULL;
int count = root->lCount + 1;
if (count == k)
return root;
if (count > k)
return kthSmallest(root->left, k);
// else search in right subtree
return kthSmallest(root->right, k - count);
}
// main function
int main()
{
Node* root = NULL;
int keys[] = { 20, 8, 22, 4, 12, 10, 14 };
for (int x : keys)
root = insert(root, x);
int k = 4;
Node* res = kthSmallest(root, k);
if (res == NULL)
cout << "There are less than k nodes in the BST";
else
cout << "K-th Smallest Element is " << res->data;
return 0;
}
// This code is contributed by Aditya Kumar (adityakumar129)
C
// A simple inorder traversal based C++ program to find k-th
// smallest element in a BST.
#include <stdio.h>
#include <stdlib.h>
// A BST node
typedef struct Node {
int data;
struct Node *left, *right;
int lCount;
} Node;
Node* new_node(int x)
{
Node* newNode = malloc(sizeof(Node));
newNode->data = x;
newNode->left = NULL;
newNode->right = NULL;
return newNode;
}
// Recursive function to insert an key into BST
Node* insert(Node* root, int x)
{
if (root == NULL)
return new_node(x);
// If a node is inserted in left subtree, then lCount of
// this node is increased. For simplicity, we are
// assuming that all keys (tried to be inserted) are
// distinct.
if (x < root->data) {
root->left = insert(root->left, x);
root->lCount++;
}
else if (x > root->data)
root->right = insert(root->right, x);
return root;
}
// Function to find k'th smallest element in BST
// Here count denotes the number of nodes processed so far
Node* kthSmallest(Node* root, int k)
{
// base case
if (root == NULL)
return NULL;
int count = root->lCount + 1;
if (count == k)
return root;
if (count > k)
return kthSmallest(root->left, k);
// else search in right subtree
return kthSmallest(root->right, k - count);
}
// main function
int main()
{
Node* root = NULL;
int keys[] = { 20, 8, 22, 4, 12, 10, 14 };
int keys_size = sizeof(keys) / sizeof(keys[0]);
for (int i = 0; i < keys_size; i++)
root = insert(root, keys[i]);
int k = 4;
Node* res = kthSmallest(root, k);
if (res == NULL)
printf("There are less than k nodes in the BST");
else
printf("K-th Smallest Element is %d", res->data);
return 0;
}
// This code is contributed by Aditya Kumar (adityakumar129)
Java
// A simple inorder traversal based Java program
// to find k-th smallest element in a BST.
import java.io.*;
import java.util.*;
// A BST node
class Node {
int data;
Node left, right;
int lCount;
Node(int x)
{
data = x;
left = right = null;
lCount = 0;
}
}
class Gfg {
// Recursive function to insert an key into BST
public static Node insert(Node root, int x)
{
if (root == null)
return new Node(x);
// If a node is inserted in left subtree, then
// lCount of this node is increased. For simplicity,
// we are assuming that all keys (tried to be
// inserted) are distinct.
if (x < root.data) {
root.left = insert(root.left, x);
root.lCount++;
}
else if (x > root.data)
root.right = insert(root.right, x);
return root;
}
// Function to find k'th largest element in BST
// Here count denotes the number of nodes processed so far
public static Node kthSmallest(Node root, int k)
{
// base case
if (root == null)
return null;
int count = root.lCount + 1;
if (count == k)
return root;
if (count > k)
return kthSmallest(root.left, k);
// else search in right subtree
return kthSmallest(root.right, k - count);
}
// main function
public static void main(String args[])
{
Node root = null;
int keys[] = { 20, 8, 22, 4, 12, 10, 14 };
for (int x : keys)
root = insert(root, x);
int k = 4;
Node res = kthSmallest(root, k);
if (res == null)
System.out.println("There are less than k nodes in the BST");
else
System.out.println("K-th Smallest Element is " + res.data);
}
}
// This code is contributed by Aditya Kumar (adityakumar129)
Python3
# A simple inorder traversal based Python3
# program to find k-th smallest element in a BST.
# A BST node
class newNode:
def __init__(self, x):
self.data = x
self.left = None
self.right = None
self.lCount = 0
# Recursive function to insert
# an key into BST
def insert(root, x):
if (root == None):
return newNode(x)
# If a node is inserted in left subtree,
# then lCount of this node is increased.
# For simplicity, we are assuming that
# all keys (tried to be inserted) are
# distinct.
if (x < root.data):
root.left = insert(root.left, x)
root.lCount += 1
elif (x > root.data):
root.right = insert(root.right, x);
return root
# Function to find k'th largest element
# in BST. Here count denotes the number
# of nodes processed so far
def kthSmallest(root, k):
# Base case
if (root == None):
return None
count = root.lCount + 1
if (count == k):
return root
if (count > k):
return kthSmallest(root.left, k)
# Else search in right subtree
return kthSmallest(root.right, k - count)
# Driver code
if __name__ == '__main__':
root = None
keys = [ 20, 8, 22, 4, 12, 10, 14 ]
for x in keys:
root = insert(root, x)
k = 4
res = kthSmallest(root, k)
if (res == None):
print("There are less than k nodes in the BST")
else:
print("K-th Smallest Element is", res.data)
# This code is contributed by bgangwar59
C#
// A simple inorder traversal based C# program
// to find k-th smallest element in a BST.
using System;
// A BST node
public class Node
{
public int data;
public Node left, right;
public int lCount;
public Node(int x)
{
data = x;
left = right = null;
lCount = 0;
}
}
class GFG{
// Recursive function to insert an key into BST
public static Node insert(Node root, int x)
{
if (root == null)
return new Node(x);
// If a node is inserted in left subtree,
// then lCount of this node is increased.
// For simplicity, we are assuming that
// all keys (tried to be inserted) are
// distinct.
if (x < root.data)
{
root.left = insert(root.left, x);
root.lCount++;
}
else if (x > root.data)
root.right = insert(root.right, x);
return root;
}
// Function to find k'th largest element
// in BST. Here count denotes the number
// of nodes processed so far
public static Node kthSmallest(Node root, int k)
{
// Base case
if (root == null)
return null;
int count = root.lCount + 1;
if (count == k)
return root;
if (count > k)
return kthSmallest(root.left, k);
// Else search in right subtree
return kthSmallest(root.right, k - count);
}
// Driver Code
public static void Main(String[] args)
{
Node root = null;
int[] keys = { 20, 8, 22, 4, 12, 10, 14 };
foreach(int x in keys)
root = insert(root, x);
int k = 4;
Node res = kthSmallest(root, k);
if (res == null)
Console.WriteLine("There are less " +
"than k nodes in the BST");
else
Console.WriteLine("K-th Smallest" +
" Element is " + res.data);
}
}
// This code is contributed by aashish1995
Javascript
<script>
// A simple inorder traversal based
// Javascript program to find k-th
// smallest element in a BST.
// A BST node
class Node
{
constructor(x)
{
this.data = x;
this.left = null;
this.right = null;
this.lCount = 0;
}
}
// Recursive function to insert an key into BST
function insert(root, x)
{
if (root == null)
return new Node(x);
// If a node is inserted in left subtree,
// then lCount of this node is increased.
// For simplicity, we are assuming that
// all keys (tried to be inserted) are
// distinct.
if (x < root.data)
{
root.left = insert(root.left, x);
root.lCount++;
}
else if (x > root.data)
root.right = insert(root.right, x);
return root;
}
// Function to find k'th largest element
// in BST. Here count denotes the number
// of nodes processed so far
function kthSmallest(root, k)
{
// Base case
if (root == null)
return null;
let count = root.lCount + 1;
if (count == k)
return root;
if (count > k)
return kthSmallest(root.left, k);
// Else search in right subtree
return kthSmallest(root.right, k - count);
}
// Driver code
let root = null;
let keys = [ 20, 8, 22, 4, 12, 10, 14 ];
for(let x = 0; x < keys.length; x++)
root = insert(root, keys[x]);
let k = 4;
let res = kthSmallest(root, k);
if (res == null)
document.write("There are less than k " +
"nodes in the BST" + "</br>");
else
document.write("K-th Smallest" +
" Element is " + res.data);
// This code is contributed by divyeshrabadiya07
</script>
K-th Smallest Element is 12
Complejidad temporal: O(h) donde h es la altura del árbol.
Publicación traducida automáticamente
Artículo escrito por GeeksforGeeks-1 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA