Dado un árbol de búsqueda binario, la tarea es encontrar el Node con el valor máximo en un BST.
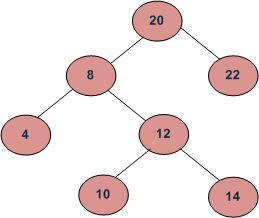
Para el árbol de arriba, comenzamos con 20, luego nos movemos a la derecha hasta 22. Seguimos moviéndonos a la derecha hasta que vemos NULL. Dado que la derecha de 22 es NULL, 22 es el Node con el valor máximo.
Enfoque: Esto es bastante simple. Simplemente atraviese el Node de la raíz a la derecha recursivamente hasta que la derecha sea NULL. El Node cuyo derecho es NULL es el Node con el valor máximo.
C++
#include <bits/stdc++.h>
using namespace std;
/* A binary tree node has data, pointer to left child
and a pointer to right child */
struct node {
int data;
struct node* left;
struct node* right;
};
// Function to create a new node
struct node* newNode(int data)
{
struct node* newnode = new node();
newnode->data = data;
newnode->left = NULL;
newnode->right = NULL;
return (newnode);
}
// Function to insert a new node in BST
struct node* insert(struct node* node, int data)
{
/* 1. If the tree is empty, return a new,
single node */
if (node == NULL)
return (newNode(data));
else {
/* 2. Otherwise, recur down the tree */
if (data <= node->data)
node->left = insert(node->left, data);
else
node->right = insert(node->right, data);
/* return the (unchanged) node pointer */
return node;
}
}
// Function to find the node with maximum value
// i.e. rightmost leaf node
int maxValue(struct node* node)
{
/* loop down to find the rightmost leaf */
struct node* current = node;
while (current->right != NULL)
current = current->right;
return (current->data);
}
// Driver code
int main()
{
struct node* root = NULL;
root = insert(root, 4);
insert(root, 2);
insert(root, 1);
insert(root, 3);
insert(root, 6);
insert(root, 5);
cout << "Maximum value in BST is " << maxValue(root);
return 0;
}
Java
// Java implementation to find the sum of last
// 'n' nodes of the Linked List
import java.util.*;
class GFG
{
/* A binary tree node has data, pointer to left child
and a pointer to right child */
static class node
{
int data;
node left;
node right;
};
// Function to create a new node
static node newNode(int data)
{
node node = new node();
node.data = data;
node.left = null;
node.right = null;
return (node);
}
// Function to insert a new node in BST
static node insert(node node, int data)
{
/* 1. If the tree is empty, return a new,
single node */
if (node == null)
return (newNode(data));
else
{
/* 2. Otherwise, recur down the tree */
if (data <= node.data)
node.left = insert(node.left, data);
else
node.right = insert(node.right, data);
/* return the (unchanged) node pointer */
return node;
}
}
// Function to find the node with maximum value
// i.e. rightmost leaf node
static int maxValue(node node)
{
/* loop down to find the rightmost leaf */
node current = node;
while (current.right != null)
current = current.right;
return (current.data);
}
// Driver code
public static void main(String[] args)
{
node root = null;
root = insert(root, 4);
insert(root, 2);
insert(root, 1);
insert(root, 3);
insert(root, 6);
insert(root, 5);
System.out.println("Maximum value in BST is " + maxValue(root));
}
}
/* This code is contributed by PrinciRaj1992 */
Python3
import sys
import math
# A binary tree node has data, pointer to left child
# and a pointer to right child
class Node:
def __init__(self,data):
self.data = data
self.left = None
self.right = None
# Function to insert a new node in BST
def insert(root, data):
# 1. If the tree is empty, return a new,
# single node
if not root:
return Node(data)
# 2. Otherwise, recur down the tree
if data < root.data:
root.left = insert(root.left, data)
if data > root.data:
root.right = insert(root.right, data)
# return the (unchanged) node pointer
return root
# Function to find the node with maximum value
# i.e. rightmost leaf node
def maxValue(root):
current = root
#loop down to find the rightmost leaf
while(current.right):
current = current.right
return current.data
# Driver code
if __name__=='__main__':
root=None
root = insert(root,2)
root = insert(root,1)
root = insert(root,3)
root = insert(root,6)
root = insert(root,5)
print("Maximum value in BST is {}".format(maxValue(root)))
# This code is contributed by Vikash Kumar 37
C#
// C# implementation to find the sum of last
// 'n' nodes of the Linked List
using System;
class GFG
{
/* A binary tree node has data, pointer to left child
and a pointer to right child */
public class node
{
public int data;
public node left;
public node right;
};
// Function to create a new node
static node newNode(int data)
{
node node = new node();
node.data = data;
node.left = null;
node.right = null;
return (node);
}
// Function to insert a new node in BST
static node insert(node node, int data)
{
/* 1. If the tree is empty, return a new,
single node */
if (node == null)
return (newNode(data));
else
{
/* 2. Otherwise, recur down the tree */
if (data <= node.data)
node.left = insert(node.left, data);
else
node.right = insert(node.right, data);
/* return the (unchanged) node pointer */
return node;
}
}
// Function to find the node with maximum value
// i.e. rightmost leaf node
static int maxValue(node node)
{
/* loop down to find the rightmost leaf */
node current = node;
while (current.right != null)
current = current.right;
return (current.data);
}
// Driver code
public static void Main(String[] args)
{
node root = null;
root = insert(root, 4);
insert(root, 2);
insert(root, 1);
insert(root, 3);
insert(root, 6);
insert(root, 5);
Console.WriteLine("Maximum value in BST is " + maxValue(root));
}
}
// This code is contributed by Rajput-Ji
Javascript
<script>
// javascript implementation to find the sum of last
// 'n' nodes of the Linked List
/*
* A binary tree node has data, pointer to left child and a pointer to right
* child
*/
class Node {
constructor(val) {
this.data = val;
this.left = null;
this.right = null;
}
}
// Function to create a new node
function newNode(data) {
var node = new Node();
node.data = data;
node.left = null;
node.right = null;
return (node);
}
// Function to insert a new node in BST
function insert( node , data) {
/*
* 1. If the tree is empty, return a new, single node
*/
if (node == null)
return (newNode(data));
else {
/* 2. Otherwise, recur down the tree */
if (data <= node.data)
node.left = insert(node.left, data);
else
node.right = insert(node.right, data);
/* return the (unchanged) node pointer */
return node;
}
}
// Function to find the node with maximum value
// i.e. rightmost leaf node
function maxValue( node) {
/* loop down to find the rightmost leaf */
var current = node;
while (current.right != null)
current = current.right;
return (current.data);
}
// Driver code
var root = null;
root = insert(root, 4);
insert(root, 2);
insert(root, 1);
insert(root, 3);
insert(root, 6);
insert(root, 5);
document.write("Maximum value in BST is " + maxValue(root));
// This code contributed by Rajput-Ji
</script>
Producción:
Maximum value in BST is 6
Complejidad de Tiempo : O(N)
Espacio Auxiliar : O(1)
Publicación traducida automáticamente
Artículo escrito por VishalBachchas y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA