Dada una array arr[] , la tarea es encontrar el único elemento restante en la array después de aplicar la siguiente operación hasta que solo quede un elemento en la array. En una operación, multiplique los elementos de contorno de esta array y si el tamaño de la array es:
- Par: inserte el producto en el medio de la array y elimine los elementos de contorno
- Impar: Reste el elemento medio del producto y reemplace el elemento medio con la diferencia absoluta y elimine los elementos de contorno.
Ejemplos:
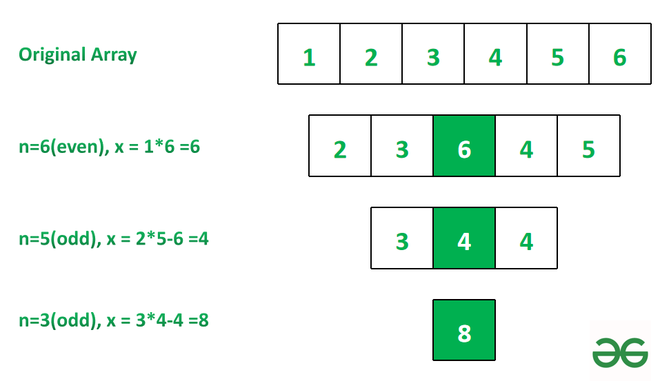
Entrada: arr[] = [ 1, 2, 3, 4, 5, 6 ]
Salida: 8
Explicación: vea la imagen a continuación para obtener una explicación.
Entrada: arr[] = [ 3, 5, 1, 8, 9]
Salida: 14
Enfoque: La solución se basa en el enfoque codicioso. Elimine los elementos de los extremos de la array e inserte los datos en el medio de la array. Ahora siga los pasos a continuación para resolver este problema:
- Ejecute un ciclo while, hasta que el tamaño de la array arr[] sea mayor que 1. En cada iteración de este ciclo:
- Tome el producto del primer y el último elemento y luego explótelos.
- Si el tamaño de la array es par, inserte el producto en el medio de la array arr[] .
- Si es impar, reste el elemento medio del producto y reemplácelo con el elemento medio.
- Después de que termine el ciclo, imprima el único elemento restante en la array.
C++
// C++ program for the baove approach
#include <bits/stdc++.h>
using namespace std;
// Function to reduce array
void PSarray(vector<int> A)
{
while (A.size() != 1) {
// If size of array is Even
if (A.size() % 2 == 0) {
// Product of boundary element
int x = A[0] * A[A.size() - 1];
A.erase(A.begin());
A.pop_back();
int n = A.size();
// Insert product in middle of element
A.insert(A.begin() + n / 2, x);
}
// Else if size of array is Odd
else {
int x = A[0] * A[A.size() - 1];
A.erase(A.begin());
A.pop_back();
int n = A.size();
// Subtract middle element from product and
// replace middle element
A[n / 2] = x - A[n / 2];
}
}
// Print the last remaining array element
cout << A[0] << endl;
}
// Driver Code
int main()
{
vector<int> arr = { 1, 2, 3, 4, 5, 6 };
PSarray(arr);
return 0;
}
// This code is contributed by Tapesh (tapeshdua420)
Java
// Java program for the baove approach
import java.util.ArrayList;
import java.util.Arrays;
class GFG
{
// Function to reduce array
static void PSarray(ArrayList<Integer> A)
{
while (A.size() != 1)
{
// If size of array is Even
if (A.size() % 2 == 0){
// Product of boundary element
int x = A.get(0)*A.get(A.size()-1);
A.remove(0);
A.remove(A.size() - 1);
int n = A.size();
// Insert product in middle of element
A.add(n/2, x);
}
// Else if size of array is Odd
else {
int x = A.get(0)*A.get(A.size() - 1);
A.remove(0);
A.remove(A.size() - 1);
int n = A.size();
// Subtract middle element from product and
// replace middle element
A.set(n / 2, x - A.get(n / 2));
}
}
// Print the last remaining array element
System.out.println(A);
}
// Driver Code
public static void main(String[] args) {
Integer []arr = {1, 2, 3, 4, 5, 6};
ArrayList<Integer> A = new ArrayList<>(Arrays.asList(arr));
PSarray(A);
}
}
// This code is contributed by shikhasingrajput
Python3
# Python program for the baove approach # Function to reduce array def PSarray(A): while len(A) != 1: # If size of array is Even if len(A) % 2 == 0: # Product of boundary element x = A.pop(0)*A.pop() n = len(A) # Insert product in middle of element A.insert(n//2, x) # Else if size of array is Odd else: x = A.pop(0)*A.pop() n = len(A) # Subtract middle element from product and # replace middle element A[n//2] = x-A[n//2] # Print the last remaining array element print(A[0]) # Driver Code if __name__ == "__main__": A = [1, 2, 3, 4, 5, 6] PSarray(A)
C#
// C# program for the baove approach
using System;
using System.Collections.Generic;
public class GFG
{
// Function to reduce array
static void PSarray(List<int> A)
{
while (A.Count != 1)
{
// If size of array is Even
if (A.Count % 2 == 0){
// Product of boundary element
int x = A[0]*A[A.Count-1];
A.RemoveAt(0);
A.RemoveAt(A.Count - 1);
int n = A.Count;
// Insert product in middle of element
A.Insert(n/2,x);
}
// Else if size of array is Odd
else {
int x = A[0]*A[A.Count - 1];
A.RemoveAt(0);
A.RemoveAt(A.Count - 1);
int n = A.Count;
// Subtract middle element from product and
// replace middle element
A[n / 2] = x - A[n / 2];
}
}
// Print the last remaining array element
A.ForEach(x=>Console.Write(x));
}
// Driver Code
public static void Main(String[] args) {
int []arr = {1, 2, 3, 4, 5, 6};
List<int> A = new List<int>(arr);
PSarray(A);
}
}
// This code is contributed by 29AjayKumar
Javascript
<script>
// JavaScript program for the baove approach
// Function to reduce array
function PSarray(A)
{
while (A.length != 1)
{
// If size of array is Even
if (A.length % 2 == 0)
{
// Product of boundary element
let x = A.shift() * A.pop()
let n = A.length
// Insert product in middle of element
let p1 = A.slice(0, Math.floor(A.length / 2))
p1.push(x)
let p2 = A.slice(Math.floor(A.length / 2))
A = p1.concat(p2)
}
// Else if size of array is Odd
else
{
let x = A.shift() * A.pop()
let n = A.length
// Subtract middle element from product and
// replace middle element
A[Math.floor(n / 2)] = x - A[Math.floor(n / 2)]
}
// Print the last remaining array element
}
document.write(A[0])
}
// Driver Code
let A = [ 1, 2, 3, 4, 5, 6 ]
PSarray(A)
// This code is contributed by Potta Lokesh
</script>
8
Complejidad de Tiempo: O(N 2 )
Espacio Auxiliar: O(1)
Publicación traducida automáticamente
Artículo escrito por harshdeepmahajan88 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA