Dado un número entero N , la tarea es encontrar el N número palindrómico par de longitud par y que solo comprende los dígitos X e Y donde X, Y > 0 .
Ejemplos:
Entrada: N = 9, X = 4, Y = 5
Salida: 454454
Explicación:
Los números palindrómicos de longitud par que usan 4 y 5 son
44, 55, 4444, 4554, 5445, 5555, 444444, 445544, 454454, …
9° término de la serie anterior = 454454
Entrada: N = 6, X = 1, Y = 2
Salida: 2222
Explicación:
Los números palindrómicos de longitud par usando 1 y 2 son
11, 22, 1111, 1221, 2112, 2222, 111111, 112211, 121121, …
6to término de la serie anterior = 2222
Acercarse:
- Los números palindrómicos de longitud par usando X e Y son
XX, YY, XXXX, XYYX, YXXY, YYYY, XXXXXX, XXYYXX, ...
- La secuencia anterior se puede observar como:
XX, -> Length (L) = 2 YY, -> Length (L) = 2 XXXX, -> Length (L) = 4 XYYX, -> Length (L) = 4 YXXY, -> Length (L) = 4 YYYY, -> Length (L) = 4 XXXXXX, -> Length (L) = 6 XXYYXX, -> Length (L) = 6 XYXXYX, -> Length (L) = 6 XYYYYX, -> Length (L) = 6 YXXXXY, -> Length (L) = 6 YXYYXY, -> Length (L) = 6 YYXXYY, -> Length (L) = 6 YYYYYY, -> Length (L) = 6 XXXXXXXX, -> Length (L) = 8 ...
- Si dividimos cualquier término en 2 mitades, la segunda mitad es justo el reverso de la primera mitad
Ejemplo:
Taking the term XXYYXX Dividing this into 2 halves XXYYXX = XXY | YXX So YXX is just the reverse of XXY
- Tomando solo la mitad izquierda de los términos y colocando X = 0 e Y = 1 para obtener la String Binaria, los números de longitud L se pueden ver formando una secuencia entera de 0 a (2 L/2 – 1), tomada como Rango (R) . Por lo tanto 0 ≤ R ≤ 2 L/2 – 1
Por lo tanto, la secuencia se puede observar de la siguiente manera:
L -> Left Half -> Binary String -> Rank (in Decimal) 2 -> X -> 0 -> 0 2 -> Y -> 1 -> 1 4 -> XX -> 00 -> 0 4 -> XY -> 01 -> 1 4 -> YX -> 10 -> 2 4 -> YY -> 11 -> 3 6 -> XXX -> 000 -> 0 6 -> XXY -> 001 -> 1 6 -> XYX -> 010 -> 2 6 -> XYY -> 011 -> 3 6 -> YXX -> 100 -> 4 6 -> YXY -> 101 -> 5 6 -> YYX -> 110 -> 6 6 -> YYY -> 111 -> 7 8 -> XXXX -> 0000 -> 0 ...
- Por lo tanto, Para el término requerido N:
- La longitud (L) del N-ésimo término requerido:
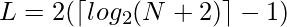
- Rango (R) del N-ésimo término requerido:
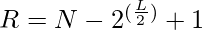
- Primera mitad del término N requerido = Representación binaria de R en L/2 bits reemplazando 0 como X y 1 como Y
- Segunda Mitad del N-ésimo término requerido = Inverso de la Primera Mitad
A continuación se muestra la implementación del enfoque anterior:
C++
// C++ program to find nth even// palindromic number of only even// length composing of 4's and 5's.#include <bits/stdc++.h>usingnamespacestd;// Utility function to compute// n'th palindrome numberstring solve(intn,charx,chary){// Calculate the length from above// formula as discussed aboveintlength =ceil(log2(n + 2)) - 1;// Calculate rank for length Lintrank = n - (1 << length) + 1;string left ="", right ="";for(inti = length - 1; i >= 0; i--) {// Mask to check if i't bit// is set or notintmask = 1 << i;// If bit is set append '5' else append '4'boolbit = mask & rank;if(bit) {left += y;right += y;}else{left += x;right += x;}}reverse(right.begin(), right.end());returnleft + right;}// Driver Codeintmain(){intn = 23;charx ='4', y ='5';string ans = solve(n, x, y);cout << ans <<'\n';return0;}Java
// Java program to find nth even// palindromic number of only even// length composing of 4's and 5's.importjava.util.*;classGFG{// Utility function to compute// n'th palindrome numberstaticString solve(intn,charx,chary){// Calculate the length from above// formula as discussed aboveintlength = (int)Math.ceil(Math.log(n +2) /Math.log(2)) -1;// Calculate rank for length Lintrank = n - (1<< length) +1;String left ="", right ="";for(inti = length -1; i >=0; i--){// Mask to check if i't bit// is set or notintmask = (1<< i);// If bit is set append '5' else append '4'intbit = mask & rank;if(bit >0){left += y;right += y;}else{left += x;right += x;}}StringBuilder sb =newStringBuilder(right);sb.reverse();right = sb.toString();String res = left + right;returnres;}// Driver Codepublicstaticvoidmain (String[] args){intn =23;charx ='4', y ='5';String ans = solve(n, x, y);System.out.println(ans);}}// This code is contributed by AnkitRai01Python3
# Python3 program to find nth even# palindromic number of only even# length composing of 4's and 5's.frommathimportceil, log2# Utility function to compute# n'th palindrome numberdefsolve(n, x, y) :# Calculate the length from above# formula as discussed abovelength=ceil(log2(n+2))-1;# Calculate rank for length Lrank=n-(1<< length)+1;left=""; right = "";foriinrange(length-1,-1,-1):# Mask to check if i't bit# is set or notmask=(1<< i);# If bit is set append '5'# else append '4'bit=(mask & rank);if(bit) :left+=y;right+=y;else:left+=x;right+=x;right=right[::-1];res=left+right;returnres;# Driver Codeif__name__=="__main__":n=23;x='4';y='5';ans=solve(n, x, y);print(ans);# This code is contributed by kanugargngC#
// C# program to find nth even// palindromic number of only even// length composing of 4's and 5's.usingSystem;classGFG{// Utility function to compute// n'th palindrome numberstaticString solve(intn,charx,chary){// Calculate the length from above// formula as discussed aboveintlength = (int)Math.Ceiling(Math.Log(n + 2) /Math.Log(2)) - 1;// Calculate rank for length Lintrank = n - (1 << length) + 1;String left ="", right ="";for(inti = length -1; i >= 0; i--){// Mask to check if i't bit// is set or notintmask = (1 << i);// If bit is set append '5'// else append '4'intbit = mask & rank;if(bit > 0){left += y;right += y;}else{left += x;right += x;}}right = reverse(right);String res = left + right;returnres;}staticString reverse(String input){char[] a = input.ToCharArray();intl, r = 0;r = a.Length - 1;for(l = 0; l < r; l++, r--){// Swap values of l and rchartemp = a[l];a[l] = a[r];a[r] = temp;}returnString.Join("", a);}// Driver CodepublicstaticvoidMain (String[] args){intn = 23;charx ='4', y ='5';String ans = solve(n, x, y);Console.WriteLine(ans);}}// This code is contributed by Rajput-JiJavaScript
<script>// Javascript program to find nth even// palindromic number of only even// length composing of 4's and 5's.// Utility function to compute// n'th palindrome numberfunctionsolve(n, x, y){// Calculate the length from above// formula as discussed abovevarlength = Math.ceil(Math.log2(n + 2)) - 1;// Calculate rank for length Lvarrank = n - (1 << length) + 1;varleft ="", right ="";for(vari = length - 1; i >= 0; i--) {// Mask to check if i't bit// is set or notvarmask = 1 << i;// If bit is set append '5' else append '4'varbit = mask & rank;if(bit) {left += y;right += y;}else{left += x;right += x;}}right = right.split('').reverse().join('');returnleft + right;}// Driver Codevarn = 23;varx ='4', y ='5';varans = solve(n, x, y);document.write( ans +"<br>");</script>Producción54444445
Complejidad de tiempo:
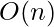 donde n es la longitud de la string
donde n es la longitud de la string
- La longitud (L) del N-ésimo término requerido: