En una tienda de dulces, hay N tipos diferentes de dulces disponibles y se proporcionan los precios de todos los N tipos diferentes de dulces. También hay una oferta atractiva por parte de la tienda de dulces. Podemos comprar un solo caramelo de la tienda y obtener como máximo K otros caramelos (todos son de diferentes tipos) gratis.
- Encuentra la cantidad mínima de dinero que tenemos que gastar para comprar todos los N dulces diferentes.
- Encuentra la cantidad máxima de dinero que tenemos que gastar para comprar todos los N dulces diferentes.
En ambos casos, debemos utilizar la oferta y recuperar el máximo de caramelos posible. Si hay k o más dulces disponibles, debemos tomar k dulces por cada compra de dulces. Si hay menos de k dulces disponibles, debemos tomar todos los dulces para una compra de dulces.
Ejemplos:
Input :
price[] = {3, 2, 1, 4}
k = 2
Output :
Min = 3, Max = 7
Explanation :
Since k is 2, if we buy one candy we can take
atmost two more for free.
So in the first case we buy the candy which
costs 1 and take candies worth 3 and 4 for
free, also you buy candy worth 2 as well.
So min cost = 1 + 2 = 3.
In the second case we buy the candy which
costs 4 and take candies worth 1 and 2 for
free, also We buy candy worth 3 as well.
So max cost = 3 + 4 = 7.
Una cosa importante a tener en cuenta es que debemos usar la oferta y recuperar el máximo de dulces por cada compra de dulces. Entonces, si queremos minimizar el dinero, debemos comprar dulces al costo mínimo y obtener dulces de costo máximo gratis. Para maximizar el dinero, debemos hacer lo contrario. A continuación se muestra un algoritmo basado en esto.
First Sort the price array. For finding minimum amount : Start purchasing candies from starting and reduce k free candies from last with every single purchase. For finding maximum amount : Start purchasing candies from the end and reduce k free candies from starting in every single purchase.
La siguiente imagen es una ilustración del enfoque anterior:
Monto minimo :

Importe máximo :
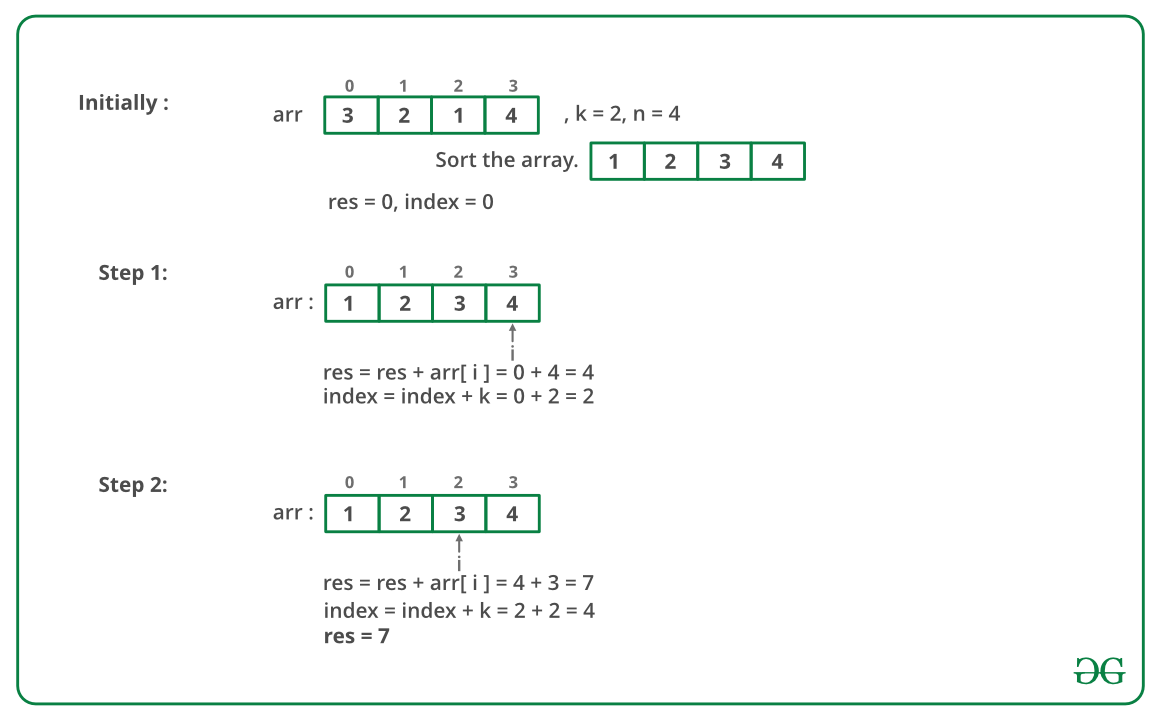
A continuación se muestra la implementación del enfoque anterior:
C++
// C++ implementation to find the minimum
// and maximum amount
#include <bits/stdc++.h>
using namespace std;
// Function to find the minimum amount
// to buy all candies
int findMinimum(int arr[], int n, int k)
{
int res = 0;
for (int i = 0; i < n; i++) {
// Buy current candy
res += arr[i];
// And take k candies for free
// from the last
n = n - k;
}
return res;
}
// Function to find the maximum amount
// to buy all candies
int findMaximum(int arr[], int n, int k)
{
int res = 0, index = 0;
for (int i = n - 1; i >= index; i--)
{
// Buy candy with maximum amount
res += arr[i];
// And get k candies for free from
// the starting
index += k;
}
return res;
}
// Driver code
int main()
{
int arr[] = { 3, 2, 1, 4 };
int n = sizeof(arr) / sizeof(arr[0]);
int k = 2;
sort(arr, arr + n);
// Function call
cout << findMinimum(arr, n, k) << " "
<< findMaximum(arr, n, k) << endl;
return 0;
}
Java
// Java implementation to find the
// minimum and maximum amount
import java.util.*;
class GFG {
// Function to find the minimum
// amount to buy all candies
static int findMinimum(int arr[], int n, int k)
{
int res = 0;
for (int i = 0; i < n; i++) {
// Buy current candy
res += arr[i];
// And take k candies for free
// from the last
n = n - k;
}
return res;
}
// Function to find the maximum
// amount to buy all candies
static int findMaximum(int arr[], int n, int k)
{
int res = 0, index = 0;
for (int i = n - 1; i >= index; i--)
{
// Buy candy with maximum amount
res += arr[i];
// And get k candies for free from
// the starting
index += k;
}
return res;
}
// Driver code
public static void main(String[] args)
{
int arr[] = { 3, 2, 1, 4 };
int n = arr.length;
int k = 2;
Arrays.sort(arr);
// Function call
System.out.println(findMinimum(arr, n, k) + " "
+ findMaximum(arr, n, k));
}
}
// This code is contributed by prerna saini
Python3
# Python implementation # to find the minimum # and maximum amount # Function to find # the minimum amount # to buy all candies def findMinimum(arr, n, k): res = 0 i = 0 while(n): # Buy current candy res += arr[i] # And take k # candies for free # from the last n = n-k i += 1 return res # Function to find # the maximum amount # to buy all candies def findMaximum(arr, n, k): res = 0 index = 0 i = n-1 while(i >= index): # Buy candy with # maximum amount res += arr[i] # And get k candies # for free from # the starting index += k i -= 1 return res # Driver code arr = [3, 2, 1, 4] n = len(arr) k = 2 arr.sort() # Function call print(findMinimum(arr, n, k), " ", findMaximum(arr, n, k)) # This code is contributed # by Anant Agarwal.
C#
// C# implementation to find the
// minimum and maximum amount
using System;
public class GFG {
// Function to find the minimum
// amount to buy all candies
static int findMinimum(int[] arr, int n, int k)
{
int res = 0;
for (int i = 0; i < n; i++)
{
// Buy current candy
res += arr[i];
// And take k candies for
// free from the last
n = n - k;
}
return res;
}
// Function to find the maximum
// amount to buy all candies
static int findMaximum(int[] arr, int n, int k)
{
int res = 0, index = 0;
for (int i = n - 1; i >= index; i--)
{
// Buy candy with maximum
// amount
res += arr[i];
// And get k candies for free
// from the starting
index += k;
}
return res;
}
// Driver code
public static void Main()
{
int[] arr = { 3, 2, 1, 4 };
int n = arr.Length;
int k = 2;
Array.Sort(arr);
// Function call
Console.WriteLine(findMinimum(arr, n, k) + " "
+ findMaximum(arr, n, k));
}
}
// This code is contributed by Sam007.
PHP
<?php
// PHP implementation to find the minimum
// and maximum amount
// Function to find the minimum amount
// to buy all candies
function findMinimum($arr, $n,$k)
{
$res = 0;
for ($i = 0; $i < $n ; $i++)
{
// Buy current candy
$res += $arr[$i];
// And take k candies for free
// from the last
$n = $n - $k;
}
return $res;
}
// Function to find the maximum amount
// to buy all candies
function findMaximum($arr, $n, $k)
{
$res = 0;
$index = 0;
for ($i = $n - 1; $i >= $index; $i--)
{
// Buy candy with maximum amount
$res += $arr[$i];
// And get k candies
// for free from
// the starting
$index += $k;
}
return $res;
}
// Driver Code
$arr = array(3, 2, 1, 4);
$n = sizeof($arr);
$k = 2;
sort($arr); sort($arr,$n);
// Function call
echo findMinimum($arr, $n, $k)," "
,findMaximum($arr, $n, $k);
return 0;
// This code is contributed by nitin mittal.
?>
Javascript
<script>
// Javascript implementation to find the
// minimum and maximum amount
// Function to find the minimum
// amount to buy all candies
function findMinimum(arr,n,k)
{
let res = 0;
for(let i = 0; i < n; i++)
{
// Buy current candy
res += arr[i];
// And take k candies for free
// from the last
n = n - k;
}
return res;
}
// Function to find the maximum
// amount to buy all candies
function findMaximum(arr,n,k)
{
let res = 0, index = 0;
for(let i = n - 1; i >= index; i--)
{
// Buy candy with maximum amount
res += arr[i];
// And get k candies for free from
// the starting
index += k;
}
return res;
}
// Driver code
let arr = [ 3, 2, 1, 4 ];
let n = arr.length;
let k = 2;
arr.sort(function(a, b){return a - b;});
// Function call
document.write(findMinimum(arr, n, k) + " " +
findMaximum(arr, n, k));
// This code is contributed by patel2127
</script>
3 7
Complejidad de tiempo : O (nlogn)
Espacio Auxiliar: O(1)
Otra implementación:
podemos usar la ayuda de la función The Least integer (función de techo) usando la función incorporada ceil() para implementar:
A continuación se muestra la implementación en Python:
C++
// C++ implementation
// to find the minimum
// and maximum amount
#include <bits/stdc++.h>
using namespace std;
// function to find the maximum
// and the minimum cost required
void find(vector<int> arr, int n, int k)
{
// Sort the array
sort(arr.begin(), arr.end());
int b = ceil(n / k * 1.0);
int min_sum = 0, max_sum = 0;
for(int i = 0; i < b; i++)
min_sum += arr[i];
for(int i = 2; i < arr.size(); i++)
max_sum += arr[i];
// print the minimum cost
cout << "minimum " << min_sum << endl;
// print the maximum cost
cout << "maximum " << max_sum << endl;
}
// Driver code
int main()
{
vector<int> arr = {3, 2, 1, 4};
int n = arr.size();
int k = 2;
// Function call
find(arr,n,k);
}
// This code is contributed by mohit kumar 29.
Java
// Java implementation to find the minimum
// and maximum amount
import java.io.*;
import java.util.Arrays;
import java.lang.Math;
class GFG{
// Function to find the maximum
// and the minimum cost required
static void find(int[] arr, int n, int k)
{
// Sort the array
Arrays.sort(arr);
int b = (int)Math.ceil(n / k * 1.0);
int min_sum = 0, max_sum = 0;
for(int i = 0; i < b; i++)
min_sum += arr[i];
for(int i = 2; i < arr.length; i++)
max_sum += arr[i];
// Print the minimum cost
System.out.println("minimum " + min_sum);
// Print the maximum cost
System.out.println("maximum " + max_sum);
}
// Driver code
public static void main (String[] args)
{
int[] arr = { 3, 2, 1, 4 };
int n = arr.length;
int k = 2;
// Function call
find(arr, n, k);
}
}
// This code is contributed by shivanisinghss2110
Python3
# Python implementation
# to find the minimum
# and maximum amount
#import ceil function
from math import ceil
# function to find the maximum
# and the minimum cost required
def find(arr,n,k):
# Sort the array
arr.sort()
b = int(ceil(n/k))
# print the minimum cost
print("minimum ",sum(arr[:b]))
# print the maximum cost
print("maximum ", sum(arr[-b:]))
# Driver Code
arr = [3, 2, 1, 4]
n = len(arr)
k = 2
# Function call
find(arr,n,k)
C#
// C# implementation to find the minimum
// and maximum amount
using System;
class GFG{
// Function to find the maximum
// and the minimum cost required
static void find(int[] arr, int n, int k)
{
// Sort the array
Array.Sort(arr);
int b = (int)Math.Ceiling(n / k * 1.0);
int min_sum = 0, max_sum = 0;
for(int i = 0; i < b; i++)
min_sum += arr[i];
for(int i = 2; i < arr.Length; i++)
max_sum += arr[i];
// Print the minimum cost
Console.WriteLine("minimum " + min_sum);
// Print the maximum cost
Console.WriteLine("maximum " + max_sum);
}
// Driver code
public static void Main()
{
int[] arr = { 3, 2, 1, 4 };
int n = arr.Length;
int k = 2;
// Function call
find(arr, n, k);
}
}
// This code is contributed by ukasp
Javascript
<script>
// JavaScript implementation
// to find the minimum
// and maximum amount
// function to find the maximum
// and the minimum cost required
function find(arr,n,k)
{
// Sort the array
arr.sort(function(a,b){return a-b;});
let b = Math.floor(Math.ceil(n/k));
let min_sum = 0, max_sum = 0;
for(let i = 0; i < b; i++)
min_sum += arr[i];
for(let i = 2; i < arr.length; i++)
max_sum += arr[i];
// print the minimum cost
document.write("minimum "+min_sum+"<br>");
// print the maximum cost
document.write("maximum "+ max_sum+"<br>");
}
// Driver Code
let arr = [3, 2, 1, 4];
let n = arr.length;
let k = 2;
// Function call
find(arr,n,k);
// This code is contributed by unknown2108
</script>
('minimum ', 3)
('maximum ', 7)
Complejidad de tiempo: O(nlog(n))
Espacio auxiliar: O(1)
Este artículo es una contribución de Sahil Chhabra . Si te gusta GeeksforGeeks y te gustaría contribuir, también puedes escribir un artículo usando write.geeksforgeeks.org o enviar tu artículo por correo a contribuido@geeksforgeeks.org. Vea su artículo que aparece en la página principal de GeeksforGeeks y ayude a otros Geeks.
Escriba comentarios si encuentra algo incorrecto o si desea compartir más información sobre el tema tratado anteriormente.
Publicación traducida automáticamente
Artículo escrito por GeeksforGeeks-1 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA