Dadas dos strings X e Y . La tarea es encontrar la longitud de la subsecuencia más larga de la string X, que es una substring en la secuencia Y.
Ejemplos:
Input : X = "ABCD", Y = "BACDBDCD" Output : 3 "ACD" is longest subsequence of X which is substring of Y. Input : X = "A", Y = "A" Output : 1
PRERREQUISITOS: El problema de la subsecuencia común más larga te ayudará a entender este problema en un abrir y cerrar de ojos 🙂
Método 1 (Fuerza Bruta):
Use la fuerza bruta para encontrar todas las subsecuencias de X y para cada subsecuencia verifique si es una substring de Y o no. Si es una substring de Y, mantenga una variable de longitud máxima y compare su longitud.
Complejidad del tiempo: O(2^n)
Método 2: (Recursión):
Sea n la longitud de X y m la longitud de Y. Haremos una función recursiva de la siguiente manera con 4 argumentos y el tipo de retorno es int, ya que obtendremos la longitud de la subsecuencia máxima posible de X, que es Substring de Y. tomará el juicio para un proceso posterior basado en el último carácter en las strings usando n-1 y m-1.
int maxSubsequenceSubstring(string &X,string &Y,int n,int m)
{
....
return ans;
}
Para la recursividad necesitamos 2 cosas, haremos que la primera sea el caso base y la segunda sea llamadas a una entrada más pequeña (para eso veremos el diagrama de elección).
CASO BASE:
Al ver el argumento de la función, podemos ver solo 2 argumentos que cambiarán durante las llamadas de recursión, es decir, las longitudes de ambas strings. Entonces, para el caso base, piense en la entrada más pequeña que podemos dar. Verá que la entrada más pequeña es 0, es decir, longitudes vacías. por lo tanto, cuando n == 0 o m == 0 es el caso base. n y m no pueden ser menores que cero. Ahora conocemos la condición y necesitamos devolver la longitud de la subsecuencia según la pregunta. si la longitud es 0, entonces significa que una de las strings está vacía y no hay una subsecuencia común posible, por lo que tenemos que devolver 0 para lo mismo.
int maxSubsequenceSubstring(string &X,string &Y,int n,int m)
{
if (n==0 || m==0) return 0;
....
return ans;
}
LLAMADAS DE NIÑOS:
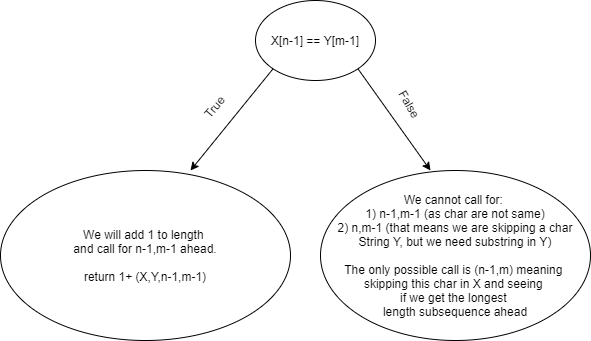
Diagrama de elección
Podemos ver cómo hacer llamadas viendo si el último carácter de ambas strings es el mismo o no. Podemos ver cómo esto es ligeramente diferente de la pregunta LCS (Subsecuencia común más larga).
int maxSubsequenceSubstring(string &X,string &Y,int n,int m)
{
// Base Case
if (n==0 || m==0) return 0;
// Calls on smaller inputs
// if the last char of both strings are equal
if(X[n-1] == Y[m-1])
{
return 1 + maxSubsequenceSubstring(X,Y,n-1,m-1);
}
// if the last char of both strings are not equal
else
{
return maxSubsequenceSubstring(X,Y,n-1,m);
}
}
Ahora aquí está el quid principal de la pregunta, podemos ver que estamos llamando a X[0..n] e Y[0..m], en nuestra función de recursión devolverá la respuesta de longitud máxima de la subsecuencia de X y Substring de Y ( y el carácter final de esa substring de Y termina en la longitud m ). Esto es muy importante ya que también queremos encontrar todas las substrings intermedias. por lo tanto, necesitamos usar un ciclo for donde llamaremos a la función anterior para todas las longitudes de 0 a m de Y, y devolveremos el máximo de la respuesta allí. Aquí está el código final en C++ para el mismo.
Implementación:
C++
#include<bits/stdc++.h>
using namespace std;
int maxSubsequenceSubstring(string &X,string &Y,int n,int m)
{
// Base Case
if (n==0 || m==0) return 0;
// Calls on smaller inputs
// if the last char of both strings are equal
if(X[n-1] == Y[m-1])
{
return 1 + maxSubsequenceSubstring(X,Y,n-1,m-1);
}
// if the last char of both strings are not equal
else
{
return maxSubsequenceSubstring(X,Y,n-1,m);
}
}
int main()
{
string X = "abcd";
string Y = "bacdbdcd";
int n = X.size(),m = Y.size();
int maximum_length = 0; //as minimum length can be 0 only.
for(int i = 0;i<=m;i++) // traversing for every length of Y.
{
int temp_ans = maxSubsequenceSubstring(X,Y,n,i);
if(temp_ans > maximum_length) maximum_length = temp_ans;
}
cout<<"Length for maximum possible Subsequence of string X which is Substring of Y -> "<<maximum_length;
return 0;
}
Java
import java.util.*;
class GFG {
static int maxSubsequenceSubString(String X, String Y,
int n, int m)
{
// Base Case
if (n == 0 || m == 0)
return 0;
// Calls on smaller inputs
// if the last char of both Strings are equal
if (X.charAt(n - 1) == Y.charAt(m - 1)) {
return 1
+ maxSubsequenceSubString(X, Y, n - 1,
m - 1);
}
// if the last char of both Strings are not equal
else {
return maxSubsequenceSubString(X, Y, n - 1, m);
}
}
// Driver code
public static void main(String[] args)
{
String X = "abcd";
String Y = "bacdbdcd";
int n = X.length(), m = Y.length();
int maximum_length
= 0; // as minimum length can be 0 only.
for (int i = 0; i <= m;
i++) // traversing for every length of Y.
{
int temp_ans
= maxSubsequenceSubString(X, Y, n, i);
if (temp_ans > maximum_length)
maximum_length = temp_ans;
}
System.out.print(
"Length for maximum possible Subsequence of String X which is SubString of Y->"
+ maximum_length);
}
}
// This code is contributed by gauravrajput1
Python3
def maxSubsequenceSubstring(X, Y, n, m):
# Base Case
if (n == 0 or m == 0):
return 0
# Calls on smaller inputs
# if the last char of both strings are equal
if(X[n - 1] == Y[m - 1]):
return 1 + maxSubsequenceSubstring(X, Y, n - 1, m - 1)
# if the last char of both strings are not equal
else:
return maxSubsequenceSubstring(X, Y, n - 1, m)
# driver code
X = "abcd"
Y = "bacdbdcd"
n, m = len(X), len(Y)
maximum_length = 0 #as minimum length can be 0 only.
for i in range(m + 1):# traversing for every length of Y.
temp_ans = maxSubsequenceSubstring(X, Y, n, i)
if(temp_ans > maximum_length):
maximum_length = temp_ans
print(f"Length for maximum possible Subsequence of string X which is Substring of Y -> {maximum_length}")
# This code is contributed by shinjanpatra
C#
using System;
public class GFG {
static int maxSubsequenceSubString(String X, String Y,
int n, int m)
{
// Base Case
if (n == 0 || m == 0)
return 0;
// Calls on smaller inputs
// if the last char of both Strings are equal
if (X[n - 1] == Y[m - 1]) {
return 1
+ maxSubsequenceSubString(X, Y, n - 1,
m - 1);
}
// if the last char of both Strings are not equal
else {
return maxSubsequenceSubString(X, Y, n - 1, m);
}
}
// Driver code
public static void Main(String[] args)
{
String X = "abcd";
String Y = "bacdbdcd";
int n = X.Length, m = Y.Length;
int maximum_length
= 0; // as minimum length can be 0 only.
for (int i = 0; i <= m;
i++) // traversing for every length of Y.
{
int temp_ans
= maxSubsequenceSubString(X, Y, n, i);
if (temp_ans > maximum_length)
maximum_length = temp_ans;
}
Console.Write(
"Length for maximum possible Subsequence of String X which is SubString of Y->"
+ maximum_length);
}
}
// This code is contributed by gauravrajput1
Javascript
<script>
function maxSubsequenceSubstring(X,Y,n,m)
{
// Base Case
if (n==0 || m==0) return 0;
// Calls on smaller inputs
// if the last char of both strings are equal
if(X[n-1] == Y[m-1])
{
return 1 + maxSubsequenceSubstring(X,Y,n-1,m-1);
}
// if the last char of both strings are not equal
else
{
return maxSubsequenceSubstring(X,Y,n-1,m);
}
}
// driver code
let X = "abcd";
let Y = "bacdbdcd";
let n = X.length,m = Y.length;
let maximum_length = 0; //as minimum length can be 0 only.
for(let i = 0;i<=m;i++) // traversing for every length of Y.
{
let temp_ans = maxSubsequenceSubstring(X,Y,n,i);
if(temp_ans > maximum_length) maximum_length = temp_ans;
}
document.write("Length for maximum possible Subsequence of string X which is Substring of Y -> "+ maximum_length);
// This code is contributed by shinjanpatra
</script>
Length for maximum possible Subsequence of string X which is Substring of Y -> 3
Complejidad de tiempo: O(n*m) (Para cada llamada en la función de recurrencia, estamos disminuyendo n, por lo tanto, alcanzaremos el caso base exactamente después de n llamadas, y estamos usando for loop para m veces para las diferentes longitudes de la string Y).
Complejidad espacial: O(n) (para las llamadas recursivas estamos usando pilas para cada llamada).
Método 3: (Programación Dinámica):
Submétodo 1: – Memoización
NOTA: Debe ver la solución de recurrencia anterior para comprender su optimización como Memoización
De la solución de recurrencia anterior, hay varias llamadas y, además, estamos usando la recursión en el bucle for, existe una alta probabilidad de que ya hayamos resuelto la respuesta para una llamada. por lo tanto, para optimizar nuestra solución de recursión que usaremos? (Vea que solo tenemos 2 argumentos que varían a lo largo de las llamadas, por lo tanto, la dimensión de la array es 2 y el tamaño se ![]() debe a que necesitamos almacenar respuestas para todas las llamadas posibles de 0..n y 0..m). Por lo tanto, es una array 2D.
debe a que necesitamos almacenar respuestas para todas las llamadas posibles de 0..n y 0..m). Por lo tanto, es una array 2D.
podemos usar el vector para la misma asignación dinámica de la array.
// initialise a vector like this
vector<vector<int>> dp(n+1,vector<int>(m+1,-1));
// or Dynamic allocation
int **dp = new int*[n+1];
for(int i = 0;i<=n;i++)
{
dp[i] = new int[m+1];
for(int j = 0;j<=m;j++)
{
dp[i][j] = -1;
}
}
Al inicializar el vector 2D, usaremos esta array como el quinto argumento en la recursividad y almacenaremos nuestra respuesta. además, lo hemos llenado con -1, lo que significa que no hemos resuelto esta llamada, por lo tanto, use la recursividad tradicional para ello, si dp[n][m] en cualquier llamada no es -1, significa que ya hemos resuelto la llamada, por lo tanto use la respuesta de dp[n][m].
// In recursion calls we will check for if we have solved the answer for the call or not
if(dp[n][m] != -1) return dp[n][m];
// Else we will store the result and return that back from this call
if(X[n-1] == Y[m-1])
return dp[n][m] = 1 + maxSubsequenceSubstring(X,Y,n-1,m-1,dp);
else
return dp[n][m] = maxSubsequenceSubstring(X,Y,n-1,m,dp);
El código para la memorización está aquí:
C++
#include<bits/stdc++.h>
using namespace std;
int maxSubsequenceSubstring(string &X,string &Y,int n,int m,vector<vector<int>>& dp)
{
// Base Case
if (n==0 || m==0) return 0;
// check if we have already solved it?
if(dp[n][m] != -1) return dp[n][m];
// Calls on smaller inputs
// if the last char of both strings are equal
if(X[n-1] == Y[m-1])
{
return dp[n][m] = 1 + maxSubsequenceSubstring(X,Y,n-1,m-1,dp);
}
// if the last char of both strings are not equal
else
{
return dp[n][m] = maxSubsequenceSubstring(X,Y,n-1,m,dp);
}
}
int main()
{
string X = "abcd";
string Y = "bacdbdcd";
int n = X.size(),m = Y.size();
int maximum_length = 0; //as minimum length can be 0 only.
vector<vector<int>> dp(n+1,vector<int>(m+1,-1));
for(int i = 0;i<=m;i++) // traversing for every length of Y.
{
int temp_ans = maxSubsequenceSubstring(X,Y,n,i,dp);
if(temp_ans > maximum_length) maximum_length = temp_ans;
}
cout<<"Length for maximum possible Subsequence of string X which is Substring of Y -> "<<maximum_length;
return 0;
}
Java
/*package whatever //do not write package name here */
import java.io.*;
import java.util.*;
class GFG {
static int maxSubsequenceSubstring(String X,String Y,int n,int m,int dp[][])
{
// Base Case
if (n==0 || m==0) return 0;
// check if we have already solved it?
if(dp[n][m] != -1) return dp[n][m];
// Calls on smaller inputs
// if the last char of both strings are equal
if(X.charAt(n-1) == Y.charAt(m-1))
{
return dp[n][m] = 1 + maxSubsequenceSubstring(X,Y,n-1,m-1,dp);
}
// if the last char of both strings are not equal
else
{
return dp[n][m] = maxSubsequenceSubstring(X,Y,n-1,m,dp);
}
}
// Driver Code
public static void main(String args[])
{
String X = "abcd";
String Y = "bacdbdcd";
int n = X.length(),m = Y.length();
int maximum_length = 0; //as minimum length can be 0 only.
int dp[][] = new int[n+1][m+1];
for(int i = 0; i < n + 1; i++){
Arrays.fill(dp[i], -1);
}
for(int i = 0;i<=m;i++) // traversing for every length of Y.
{
int temp_ans = maxSubsequenceSubstring(X,Y,n,i,dp);
if(temp_ans > maximum_length) maximum_length = temp_ans;
}
System.out.println("Length for maximum possible Subsequence of string X which is Substring of Y -> "+maximum_length);
}
}
// This code is contributed by shinjanpatra
Python3
# Python implementation of above approach
def maxSubsequenceSubstring(X, Y, n, m, dp):
# Base Case
if (n == 0 or m == 0):
return 0
# check if we have already solved it?
if(dp[n][m] != -1):
return dp[n][m]
# Calls on smaller inputs
# if the last char of both strings are equal
if(X[n - 1] == Y[m - 1]):
dp[n][m] = 1 + maxSubsequenceSubstring(X, Y, n - 1, m - 1, dp)
return dp[n][m]
# if the last char of both strings are not equal
else:
dp[n][m] = maxSubsequenceSubstring(X, Y, n - 1, m, dp)
return dp[n][m]
# driver code
X = "abcd"
Y = "bacdbdcd"
n,m = len(X),len(Y)
maximum_length = 0 #as minimum length can be 0 only.
dp = [[-1 for i in range(m+1)]for j in range(n+1)]
for i in range(m+1): # traversing for every length of Y.
temp_ans = maxSubsequenceSubstring(X, Y, n, i, dp)
if(temp_ans > maximum_length):
maximum_length = temp_ans
print("Length for maximum possible Subsequence of string X which is Substring of Y -> "+str(maximum_length))
# This code is contributed by shinjanpatra
Javascript
<script>
// JavaScript implementation of above approach
function maxSubsequenceSubstring(X,Y,n,m,dp)
{
// Base Case
if (n==0 || m==0) return 0;
// check if we have already solved it?
if(dp[n][m] != -1) return dp[n][m];
// Calls on smaller inputs
// if the last char of both strings are equal
if(X[n-1] == Y[m-1])
{
return dp[n][m] = 1 + maxSubsequenceSubstring(X,Y,n-1,m-1,dp);
}
// if the last char of both strings are not equal
else
{
return dp[n][m] = maxSubsequenceSubstring(X,Y,n-1,m,dp);
}
}
// driver code
let X = "abcd";
let Y = "bacdbdcd";
let n = X.length,m = Y.length;
let maximum_length = 0; //as minimum length can be 0 only.
let dp = new Array(n+1);
for(let i=0;i<n+1;i++){
dp[i] = new Array(m+1).fill(-1);
}
for(let i = 0;i<=m;i++) // traversing for every length of Y.
{
let temp_ans = maxSubsequenceSubstring(X,Y,n,i,dp);
if(temp_ans > maximum_length) maximum_length = temp_ans;
}
document.write("Length for maximum possible Subsequence of string X which is Substring of Y -> ",maximum_length);
// This code is contributed by shinjanpatra
</script>
Length for maximum possible Subsequence of string X which is Substring of Y -> 3
Complejidad de tiempo: O(n*m) (Definitivamente será mejor que la solución recursiva, el peor de los casos solo es posible cuando ninguno de los caracteres de la string X está en la String Y)
. Complejidad de espacio: O(n*m + n) (el tamaño de la array Dp y el tamaño de llamada de pila de la recursividad)
Submétodo 2: Tabulación
Sea n la longitud de X y m la longitud de Y. Cree una array 2D ‘dp[][]’ de m + 1 filas y n + 1 columnas. El valor dp[i][j] es la longitud máxima de la subsecuencia de X[0….j] que es la substring de Y[0….i]. Ahora, para cada celda de dp[][], complete el valor como:
for (i = 1 to m)
for (j = 1 to n)
if (x[i-1] == y[j - 1])
dp[i][j] = dp[i-1][j-1] + 1;
else
dp[i][j] = dp[i][j-1];
Y finalmente, la longitud de la subsecuencia más larga de x que es una substring de y es max(dp[i][n]) donde 1 <= i <= m.
A continuación se muestra la implementación de este enfoque:
C++
// C++ code to implement the approach
#include <bits/stdc++.h>
using namespace std;
const int MAX = 1000;
// Return the maximum size of substring of
// X which is substring in Y.
int maxSubsequenceSubstring(string x,string y,int n,int m)
{
vector<vector<int>>dp(MAX,vector<int>(MAX,0));
// Calculating value for each element.
for (int i = 1; i <= m; i++) {
for (int j = 1; j <= n; j++) {
// If alphabet of string X and Y are
// equal make dp[i][j] = 1 + dp[i-1][j-1]
if (x[j - 1] == y[i - 1])
dp[i][j] = 1 + dp[i - 1][j - 1];
// Else copy the previous value in the
// row i.e dp[i-1][j-1]
else
dp[i][j] = dp[i][j - 1];
}
}
// Finding the maximum length.
int ans = 0;
for (int i = 1; i <= m; i++)
ans = max(ans, dp[i][n]);
return ans;
}
// Driver code
int main()
{
string x = "ABCD";
string y = "BACDBDCD";
int n = x.length(), m = y.length();
cout<<maxSubsequenceSubstring(x, y, n, m);
}
// This code is contributed by shinjanpatra
Java
// Java program to find maximum length of
// subsequence of a string X such it is
// substring in another string Y.
public class GFG
{
static final int MAX = 1000;
// Return the maximum size of substring of
// X which is substring in Y.
static int maxSubsequenceSubstring(char x[], char y[],
int n, int m)
{
int dp[][] = new int[MAX][MAX];
// Initialize the dp[][] to 0.
for (int i = 0; i <= m; i++)
for (int j = 0; j <= n; j++)
dp[i][j] = 0;
// Calculating value for each element.
for (int i = 1; i <= m; i++) {
for (int j = 1; j <= n; j++) {
// If alphabet of string X and Y are
// equal make dp[i][j] = 1 + dp[i-1][j-1]
if (x[j - 1] == y[i - 1])
dp[i][j] = 1 + dp[i - 1][j - 1];
// Else copy the previous value in the
// row i.e dp[i-1][j-1]
else
dp[i][j] = dp[i][j - 1];
}
}
// Finding the maximum length.
int ans = 0;
for (int i = 1; i <= m; i++)
ans = Math.max(ans, dp[i][n]);
return ans;
}
// Driver Method
public static void main(String[] args)
{
char x[] = "ABCD".toCharArray();
char y[] = "BACDBDCD".toCharArray();
int n = x.length, m = y.length;
System.out.println(maxSubsequenceSubstring(x, y, n, m));
}
}
Python3
# Python3 program to find maximum # length of subsequence of a string # X such it is substring in another # string Y. MAX = 1000 # Return the maximum size of # substring of X which is # substring in Y. def maxSubsequenceSubstring(x, y, n, m): dp = [[0 for i in range(MAX)] for i in range(MAX)] # Initialize the dp[][] to 0. # Calculating value for each element. for i in range(1, m + 1): for j in range(1, n + 1): # If alphabet of string # X and Y are equal make # dp[i][j] = 1 + dp[i-1][j-1] if(x[j - 1] == y[i - 1]): dp[i][j] = 1 + dp[i - 1][j - 1] # Else copy the previous value # in the row i.e dp[i-1][j-1] else: dp[i][j] = dp[i][j - 1] # Finding the maximum length ans = 0 for i in range(1, m + 1): ans = max(ans, dp[i][n]) return ans # Driver Code x = "ABCD" y = "BACDBDCD" n = len(x) m = len(y) print(maxSubsequenceSubstring(x, y, n, m)) # This code is contributed # by sahilshelangia
C#
// C# program to find maximum length of
// subsequence of a string X such it is
// substring in another string Y.
using System;
public class GFG
{
static int MAX = 1000;
// Return the maximum size of substring of
// X which is substring in Y.
static int maxSubsequenceSubstring(string x, string y,
int n, int m)
{
int[ ,]dp = new int[MAX, MAX];
// Initialize the dp[][] to 0.
for (int i = 0; i <= m; i++)
for (int j = 0; j <= n; j++)
dp[i, j] = 0;
// Calculating value for each element.
for (int i = 1; i <= m; i++) {
for (int j = 1; j <= n; j++) {
// If alphabet of string X and Y are
// equal make dp[i][j] = 1 + dp[i-1][j-1]
if (x[j - 1] == y[i - 1])
dp[i, j] = 1 + dp[i - 1, j - 1];
// Else copy the previous value in the
// row i.e dp[i-1][j-1]
else
dp[i, j] = dp[i, j - 1];
}
}
// Finding the maximum length.
int ans = 0;
for (int i = 1; i <= m; i++)
ans = Math.Max(ans, dp[i,n]);
return ans;
}
// Driver Method
public static void Main()
{
string x = "ABCD";
string y = "BACDBDCD";
int n = x.Length, m = y.Length;
Console.WriteLine(maxSubsequenceSubstring(x,
y, n, m));
}
}
// This code is contributed by vt_m.
PHP
<?php
// PHP program to find maximum length of
// subsequence of a string X such it is
// substring in another string Y.
// Return the maximum size of substring of
// X which is substring in Y.
function maxSubsequenceSubstring($x, $y,
$n, $m)
{
$dp;
// Initialize the dp[][] to 0.
for ($i = 0; $i <= $m; $i++)
for ($j = 0; $j <= $n; $j++)
$dp[$i][$j] = 0;
// Calculating value for each element.
for ($i = 1; $i <= $m; $i++) {
for ( $j = 1; $j <= $n; $j++) {
// If alphabet of string
// X and Y are equal make
// dp[i][j] = 1 + dp[i-1][j-1]
if ($x[$j - 1] == $y[$i - 1])
$dp[$i][$j] = 1 + $dp[$i - 1][$j - 1];
// Else copy the previous
// value in the
// row i.e dp[i-1][j-1]
else
$dp[$i][$j] = $dp[$i][$j - 1];
}
}
// Finding the maximum length.
$ans = 0;
for ( $i = 1; $i <= $m; $i++)
$ans = max($ans, $dp[$i][$n]);
return $ans;
}
// Driver Code
{
$x = "ABCD";
$y = "BACDBDCD";
$n = strlen($x); $m = strlen($y);
echo maxSubsequenceSubstring($x, $y, $n, $m);
return 0;
}
// This code is contributed by nitin mittal
?>
Javascript
<script>
// Javascript program to find maximum length of
// subsequence of a string X such it is
// substring in another string Y.
var MAX = 1000;
// Return the maximum size of substring of
// X which is substring in Y.
function maxSubsequenceSubstring(x, y, n, m)
{
var dp = Array.from(Array(MAX), ()=> Array(MAX));
// Initialize the dp[][] to 0.
for (var i = 0; i <= m; i++)
for (var j = 0; j <= n; j++)
dp[i][j] = 0;
// Calculating value for each element.
for (var i = 1; i <= m; i++) {
for (var j = 1; j <= n; j++) {
// If alphabet of string X and Y are
// equal make dp[i][j] = 1 + dp[i-1][j-1]
if (x[j - 1] == y[i - 1])
dp[i][j] = 1 + dp[i - 1][j - 1];
// Else copy the previous value in the
// row i.e dp[i-1][j-1]
else
dp[i][j] = dp[i][j - 1];
}
}
// Finding the maximum length.
var ans = 0;
for (var i = 1; i <= m; i++)
ans = Math.max(ans, dp[i][n]);
return ans;
}
// Driver Program
var x = "ABCD";
var y = "BACDBDCD";
var n = x.length, m = y.length;
document.write( maxSubsequenceSubstring(x, y, n, m));
</script>
3
Complejidad de tiempo: O(n*m) (Tiempo requerido para llenar la array Dp)
Complejidad de espacio: O(n*m + n) (el tamaño de la array Dp)
Este artículo es una contribución de Anuj Chauhan . Si te gusta GeeksforGeeks y te gustaría contribuir, también puedes escribir un artículo usando write.geeksforgeeks.org o enviar tu artículo por correo a review-team@geeksforgeeks.org. Vea su artículo que aparece en la página principal de GeeksforGeeks y ayude a otros Geeks.
Publicación traducida automáticamente
Artículo escrito por GeeksforGeeks-1 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA