Dado un árbol de búsqueda binario, encuentre la mediana de él.
Si no. de Nodes son pares: entonces mediana = ((n/2º Node + ((n)/2º+1) Node) /2
Si el número de Nodes es impar: entonces mediana = (n+1)/2º Node.
Por ejemplo , la mediana de debajo de BST es 12.
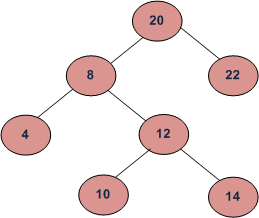
Más ejemplos:
Given BST(with odd no. of nodes) is :
6
/ \
3 8
/ \ / \
1 4 7 9
Inorder of Given BST will be : 1, 3, 4, 6, 7, 8, 9
So, here median will 6.
Given BST(with even no. of nodes) is :
6
/ \
3 8
/ \ /
1 4 7
Inorder of Given BST will be : 1, 3, 4, 6, 7, 8
So, here median will (4+6)/2 = 5.
Preguntado en: Google
Para encontrar la mediana, necesitamos encontrar el Inorder del BST porque su Inorder estará ordenado y luego encontrar la mediana, es decir
, la idea se basa en el elemento más pequeño K’th en BST usando O (1) Extra Space
La tarea es muy simple si se nos permite usar espacio adicional pero el recorrido en orden usando recursividad y pila usan espacio que no está permitido aquí. Entonces, la solución es hacer un recorrido Morris Inorder ya que no requiere espacio adicional.
Implementation: 1- Count the no. of nodes in the given BST using Morris Inorder Traversal. 2- Then Perform Morris Inorder traversal one more time by counting nodes and by checking if count is equal to the median point. To consider even no. of nodes an extra pointer pointing to the previous node is used.
C++
/* C++ program to find the median of BST in O(n)
time and O(1) space*/
#include<bits/stdc++.h>
using namespace std;
/* A binary search tree Node has data, pointer
to left child and a pointer to right child */
struct Node
{
int data;
struct Node* left, *right;
};
// A utility function to create a new BST node
struct Node *newNode(int item)
{
struct Node *temp = new Node;
temp->data = item;
temp->left = temp->right = NULL;
return temp;
}
/* A utility function to insert a new node with
given key in BST */
struct Node* insert(struct Node* node, int key)
{
/* If the tree is empty, return a new node */
if (node == NULL) return newNode(key);
/* Otherwise, recur down the tree */
if (key < node->data)
node->left = insert(node->left, key);
else if (key > node->data)
node->right = insert(node->right, key);
/* return the (unchanged) node pointer */
return node;
}
/* Function to count nodes in a binary search tree
using Morris Inorder traversal*/
int counNodes(struct Node *root)
{
struct Node *current, *pre;
// Initialise count of nodes as 0
int count = 0;
if (root == NULL)
return count;
current = root;
while (current != NULL)
{
if (current->left == NULL)
{
// Count node if its left is NULL
count++;
// Move to its right
current = current->right;
}
else
{
/* Find the inorder predecessor of current */
pre = current->left;
while (pre->right != NULL &&
pre->right != current)
pre = pre->right;
/* Make current as right child of its
inorder predecessor */
if(pre->right == NULL)
{
pre->right = current;
current = current->left;
}
/* Revert the changes made in if part to
restore the original tree i.e., fix
the right child of predecessor */
else
{
pre->right = NULL;
// Increment count if the current
// node is to be visited
count++;
current = current->right;
} /* End of if condition pre->right == NULL */
} /* End of if condition current->left == NULL*/
} /* End of while */
return count;
}
/* Function to find median in O(n) time and O(1) space
using Morris Inorder traversal*/
int findMedian(struct Node *root)
{
if (root == NULL)
return 0;
int count = counNodes(root);
int currCount = 0;
struct Node *current = root, *pre, *prev;
while (current != NULL)
{
if (current->left == NULL)
{
// count current node
currCount++;
// check if current node is the median
// Odd case
if (count % 2 != 0 && currCount == (count+1)/2)
return prev->data;
// Even case
else if (count % 2 == 0 && currCount == (count/2)+1)
return (prev->data + current->data)/2;
// Update prev for even no. of nodes
prev = current;
//Move to the right
current = current->right;
}
else
{
/* Find the inorder predecessor of current */
pre = current->left;
while (pre->right != NULL && pre->right != current)
pre = pre->right;
/* Make current as right child of its inorder predecessor */
if (pre->right == NULL)
{
pre->right = current;
current = current->left;
}
/* Revert the changes made in if part to restore the original
tree i.e., fix the right child of predecessor */
else
{
pre->right = NULL;
prev = pre;
// Count current node
currCount++;
// Check if the current node is the median
if (count % 2 != 0 && currCount == (count+1)/2 )
return current->data;
else if (count%2==0 && currCount == (count/2)+1)
return (prev->data+current->data)/2;
// update prev node for the case of even
// no. of nodes
prev = current;
current = current->right;
} /* End of if condition pre->right == NULL */
} /* End of if condition current->left == NULL*/
} /* End of while */
}
/* Driver program to test above functions*/
int main()
{
/* Let us create following BST
50
/ \
30 70
/ \ / \
20 40 60 80 */
struct Node *root = NULL;
root = insert(root, 50);
insert(root, 30);
insert(root, 20);
insert(root, 40);
insert(root, 70);
insert(root, 60);
insert(root, 80);
cout << "\nMedian of BST is "
<< findMedian(root);
return 0;
}
Java
/* Java program to find the median of BST in O(n)
time and O(1) space*/
class GfG {
/* A binary search tree Node has data, pointer
to left child and a pointer to right child */
static class Node
{
int data;
Node left, right;
}
// A utility function to create a new BST node
static Node newNode(int item)
{
Node temp = new Node();
temp.data = item;
temp.left = null;
temp.right = null;
return temp;
}
/* A utility function to insert a new node with
given key in BST */
static Node insert(Node node, int key)
{
/* If the tree is empty, return a new node */
if (node == null) return newNode(key);
/* Otherwise, recur down the tree */
if (key < node.data)
node.left = insert(node.left, key);
else if (key > node.data)
node.right = insert(node.right, key);
/* return the (unchanged) node pointer */
return node;
}
/* Function to count nodes in a binary search tree
using Morris Inorder traversal*/
static int counNodes(Node root)
{
Node current, pre;
// Initialise count of nodes as 0
int count = 0;
if (root == null)
return count;
current = root;
while (current != null)
{
if (current.left == null)
{
// Count node if its left is NULL
count++;
// Move to its right
current = current.right;
}
else
{
/* Find the inorder predecessor of current */
pre = current.left;
while (pre.right != null &&
pre.right != current)
pre = pre.right;
/* Make current as right child of its
inorder predecessor */
if(pre.right == null)
{
pre.right = current;
current = current.left;
}
/* Revert the changes made in if part to
restore the original tree i.e., fix
the right child of predecessor */
else
{
pre.right = null;
// Increment count if the current
// node is to be visited
count++;
current = current.right;
} /* End of if condition pre->right == NULL */
} /* End of if condition current->left == NULL*/
} /* End of while */
return count;
}
/* Function to find median in O(n) time and O(1) space
using Morris Inorder traversal*/
static int findMedian(Node root)
{
if (root == null)
return 0;
int count = counNodes(root);
int currCount = 0;
Node current = root, pre = null, prev = null;
while (current != null)
{
if (current.left == null)
{
// count current node
currCount++;
// check if current node is the median
// Odd case
if (count % 2 != 0 && currCount == (count+1)/2)
return prev.data;
// Even case
else if (count % 2 == 0 && currCount == (count/2)+1)
return (prev.data + current.data)/2;
// Update prev for even no. of nodes
prev = current;
//Move to the right
current = current.right;
}
else
{
/* Find the inorder predecessor of current */
pre = current.left;
while (pre.right != null && pre.right != current)
pre = pre.right;
/* Make current as right child of its inorder predecessor */
if (pre.right == null)
{
pre.right = current;
current = current.left;
}
/* Revert the changes made in if part to restore the original
tree i.e., fix the right child of predecessor */
else
{
pre.right = null;
prev = pre;
// Count current node
currCount++;
// Check if the current node is the median
if (count % 2 != 0 && currCount == (count+1)/2 )
return current.data;
else if (count%2==0 && currCount == (count/2)+1)
return (prev.data+current.data)/2;
// update prev node for the case of even
// no. of nodes
prev = current;
current = current.right;
} /* End of if condition pre->right == NULL */
} /* End of if condition current->left == NULL*/
} /* End of while */
return -1;
}
/* Driver code*/
public static void main(String[] args)
{
/* Let us create following BST
50
/ \
30 70
/ \ / \
20 40 60 80 */
Node root = null;
root = insert(root, 50);
insert(root, 30);
insert(root, 20);
insert(root, 40);
insert(root, 70);
insert(root, 60);
insert(root, 80);
System.out.println("Median of BST is " + findMedian(root));
}
}
// This code is contributed by prerna saini.
Python3
# Python program to find closest
# value in Binary search Tree
_MIN=-2147483648
_MAX=2147483648
# Helper function that allocates
# a new node with the given data
# and None left and right pointers.
class newNode:
# Constructor to create a new node
def __init__(self, data):
self.data = data
self.left = None
self.right = None
""" A utility function to insert a new node with
given key in BST """
def insert(node,key):
""" If the tree is empty, return a new node """
if (node == None):
return newNode(key)
""" Otherwise, recur down the tree """
if (key < node.data):
node.left = insert(node.left, key)
elif (key > node.data):
node.right = insert(node.right, key)
""" return the (unchanged) node pointer """
return node
""" Function to count nodes in
a binary search tree using
Morris Inorder traversal"""
def counNodes(root):
# Initialise count of nodes as 0
count = 0
if (root == None):
return count
current = root
while (current != None):
if (current.left == None):
# Count node if its left is None
count+=1
# Move to its right
current = current.right
else:
""" Find the inorder predecessor of current """
pre = current.left
while (pre.right != None and
pre.right != current):
pre = pre.right
""" Make current as right child of its
inorder predecessor """
if(pre.right == None):
pre.right = current
current = current.left
else:
pre.right = None
# Increment count if the current
# node is to be visited
count += 1
current = current.right
return count
""" Function to find median in
O(n) time and O(1) space
using Morris Inorder traversal"""
def findMedian(root):
if (root == None):
return 0
count = counNodes(root)
currCount = 0
current = root
while (current != None):
if (current.left == None):
# count current node
currCount += 1
# check if current node is the median
# Odd case
if (count % 2 != 0 and
currCount == (count + 1)//2):
return prev.data
# Even case
elif (count % 2 == 0 and
currCount == (count//2)+1):
return (prev.data + current.data)//2
# Update prev for even no. of nodes
prev = current
#Move to the right
current = current.right
else:
""" Find the inorder predecessor of current """
pre = current.left
while (pre.right != None and
pre.right != current):
pre = pre.right
""" Make current as right child
of its inorder predecessor """
if (pre.right == None):
pre.right = current
current = current.left
else:
pre.right = None
prev = pre
# Count current node
currCount+= 1
# Check if the current node is the median
if (count % 2 != 0 and
currCount == (count + 1) // 2 ):
return current.data
elif (count%2 == 0 and
currCount == (count // 2) + 1):
return (prev.data+current.data)//2
# update prev node for the case of even
# no. of nodes
prev = current
current = current.right
# Driver Code
if __name__ == '__main__':
""" Constructed binary tree is
50
/ \
30 70
/ \ / \
20 40 60 80 """
root = newNode(50)
insert(root, 30)
insert(root, 20)
insert(root, 40)
insert(root, 70)
insert(root, 60)
insert(root, 80)
print("Median of BST is ",findMedian(root))
# This code is contributed
# Shubham Singh(SHUBHAMSINGH10)
C#
/* C# program to find the median of BST in O(n)
time and O(1) space*/
using System;
class GfG
{
/* A binary search tree Node has data, pointer
to left child and a pointer to right child */
public class Node
{
public int data;
public Node left, right;
}
// A utility function to create a new BST node
static Node newNode(int item)
{
Node temp = new Node();
temp.data = item;
temp.left = null;
temp.right = null;
return temp;
}
/* A utility function to insert a new node with
given key in BST */
static Node insert(Node node, int key)
{
/* If the tree is empty, return a new node */
if (node == null) return newNode(key);
/* Otherwise, recur down the tree */
if (key < node.data)
node.left = insert(node.left, key);
else if (key > node.data)
node.right = insert(node.right, key);
/* return the (unchanged) node pointer */
return node;
}
/* Function to count nodes in a binary search tree
using Morris Inorder traversal*/
static int counNodes(Node root)
{
Node current, pre;
// Initialise count of nodes as 0
int count = 0;
if (root == null)
return count;
current = root;
while (current != null)
{
if (current.left == null)
{
// Count node if its left is NULL
count++;
// Move to its right
current = current.right;
}
else
{
/* Find the inorder predecessor of current */
pre = current.left;
while (pre.right != null &&
pre.right != current)
pre = pre.right;
/* Make current as right child of its
inorder predecessor */
if(pre.right == null)
{
pre.right = current;
current = current.left;
}
/* Revert the changes made in if part to
restore the original tree i.e., fix
the right child of predecessor */
else
{
pre.right = null;
// Increment count if the current
// node is to be visited
count++;
current = current.right;
} /* End of if condition pre->right == NULL */
} /* End of if condition current->left == NULL*/
} /* End of while */
return count;
}
/* Function to find median in O(n) time and O(1) space
using Morris Inorder traversal*/
static int findMedian(Node root)
{
if (root == null)
return 0;
int count = counNodes(root);
int currCount = 0;
Node current = root, pre = null, prev = null;
while (current != null)
{
if (current.left == null)
{
// count current node
currCount++;
// check if current node is the median
// Odd case
if (count % 2 != 0 && currCount == (count+1)/2)
return prev.data;
// Even case
else if (count % 2 == 0 && currCount == (count/2)+1)
return (prev.data + current.data)/2;
// Update prev for even no. of nodes
prev = current;
//Move to the right
current = current.right;
}
else
{
/* Find the inorder predecessor of current */
pre = current.left;
while (pre.right != null && pre.right != current)
pre = pre.right;
/* Make current as right child of its inorder predecessor */
if (pre.right == null)
{
pre.right = current;
current = current.left;
}
/* Revert the changes made in if part to restore the original
tree i.e., fix the right child of predecessor */
else
{
pre.right = null;
prev = pre;
// Count current node
currCount++;
// Check if the current node is the median
if (count % 2 != 0 && currCount == (count+1)/2 )
return current.data;
else if (count % 2 == 0 && currCount == (count/2)+1)
return (prev.data + current.data)/2;
// update prev node for the case of even
// no. of nodes
prev = current;
current = current.right;
} /* End of if condition pre->right == NULL */
} /* End of if condition current->left == NULL*/
} /* End of while */
return -1;
}
/* Driver code*/
public static void Main(String []args)
{
/* Let us create following BST
50
/ \
30 70
/ \ / \
20 40 60 80 */
Node root = null;
root = insert(root, 50);
insert(root, 30);
insert(root, 20);
insert(root, 40);
insert(root, 70);
insert(root, 60);
insert(root, 80);
Console.WriteLine("Median of BST is " + findMedian(root));
}
}
// This code is contributed by Arnab Kundu
Javascript
<script>
/* JavaScript program to find
the median of BST in O(n)
time and O(1) space*/
/* A binary search tree Node has data, pointer
to left child and a pointer to right child */
class Node {
constructor() {
this.data = 0;
this.left = null;
this.right = null;
}
}
// A utility function to create a new BST node
function newNode(item)
{
var temp = new Node();
temp.data = item;
temp.left = null;
temp.right = null;
return temp;
}
/* A utility function to insert a new node with
given key in BST */
function insert(node , key)
{
/* If the tree is empty, return a new node */
if (node == null) return newNode(key);
/* Otherwise, recur down the tree */
if (key < node.data)
node.left = insert(node.left, key);
else if (key > node.data)
node.right = insert(node.right, key);
/* return the (unchanged) node pointer */
return node;
}
/* Function to count nodes in a binary search tree
using Morris Inorder traversal*/
function counNodes(root)
{
var current, pre;
// Initialise count of nodes as 0
var count = 0;
if (root == null)
return count;
current = root;
while (current != null)
{
if (current.left == null)
{
// Count node if its left is NULL
count++;
// Move to its right
current = current.right;
}
else
{
/* Find the inorder predecessor of current */
pre = current.left;
while (pre.right != null &&
pre.right != current)
pre = pre.right;
/* Make current as right child of its
inorder predecessor */
if(pre.right == null)
{
pre.right = current;
current = current.left;
}
/* Revert the changes made in if part to
restore the original tree i.e., fix
the right child of predecessor */
else
{
pre.right = null;
// Increment count if the current
// node is to be visited
count++;
current = current.right;
} /* End of if condition pre->right == NULL */
} /* End of if condition current->left == NULL*/
} /* End of while */
return count;
} /* Function to find median in O(n) time and O(1) space
using Morris Inorder traversal*/
function findMedian(root)
{
if (root == null)
return 0;
var count = counNodes(root);
var currCount = 0;
var current = root, pre = null, prev = null;
while (current != null)
{
if (current.left == null)
{
// count current node
currCount++;
// check if current node is the median
// Odd case
if (count % 2 != 0 &&
currCount == (count+1)/2)
return prev.data;
// Even case
else if (count % 2 == 0 &&
currCount == (count/2)+1)
return (prev.data + current.data)/2;
// Update prev for even no. of nodes
prev = current;
//Move to the right
current = current.right;
}
else
{
/* Find the inorder predecessor of current */
pre = current.left;
while (pre.right != null &&
pre.right != current)
pre = pre.right;
/* Make current as right child of its
inorder predecessor */
if (pre.right == null)
{
pre.right = current;
current = current.left;
}
/* Revert the changes made in if
part to restore the original
tree i.e., fix the right child of predecessor */
else
{
pre.right = null;
prev = pre;
// Count current node
currCount++;
// Check if the current node is the median
if (count % 2 != 0 &&
currCount == (count+1)/2 )
return current.data;
else if (count%2==0 &&
currCount == (count/2)+1)
return (prev.data+current.data)/2;
// update prev node for the case of even
// no. of nodes
prev = current;
current = current.right;
} /* End of if condition pre->right == NULL */
} /* End of if condition current->left == NULL*/
} /* End of while */
return -1;
}
/* Driver code*/
/* Let us create following BST
50
/ \
30 70
/ \ / \
20 40 60 80 */
var root = null;
root = insert(root, 50);
insert(root, 30);
insert(root, 20);
insert(root, 40);
insert(root, 70);
insert(root, 60);
insert(root, 80);
document.write("Median of BST is " + findMedian(root));
// This code is contributed by todaysgaurav
</script>
Producción:
Median of BST is 50
Referencia:
https://www.careercup.com/question?id=4882624968392704
Este artículo es una contribución de Sahil Chhabra . Si te gusta GeeksforGeeks y te gustaría contribuir, también puedes escribir un artículo usando write.geeksforgeeks.org o enviar tu artículo por correo a review-team@geeksforgeeks.org. Vea su artículo que aparece en la página principal de GeeksforGeeks y ayude a otros Geeks.
Escriba comentarios si encuentra algo incorrecto o si desea compartir más información sobre el tema tratado anteriormente.
Publicación traducida automáticamente
Artículo escrito por GeeksforGeeks-1 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA