Dado un gráfico, un vértice fuente en el gráfico y un número k, encuentre si hay un camino simple (sin ningún ciclo) que comience desde la fuente dada y termine en cualquier otro vértice tal que la distancia desde la fuente hasta ese vértice sea al menos ‘k ‘ longitud.
Example:
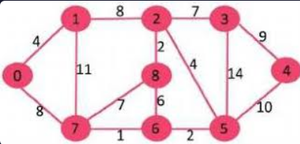
Gráfico no dirigido ponderado
Input : Source s = 0, k = 58 Output : True There exists a simple path 0 -> 7 -> 1 -> 2 -> 8 -> 6 -> 5 -> 3 -> 4 Which has a total distance of 60 km which is more than 58. Input : Source s = 0, k = 62 Output : False In the above graph, the longest simple path has distance 61 (0 -> 7 -> 1-> 2 -> 3 -> 4 -> 5-> 6 -> 8, so output should be false for any input greater than 61.
Le recomendamos encarecidamente que minimice su navegador y que pruebe esto usted mismo primero.
Una cosa importante a tener en cuenta es que simplemente hacer BFS o DFS y elegir el borde más largo en cada paso no funcionaría. La razón es que un borde más corto puede producir una ruta más larga debido a los bordes de mayor peso conectados a través de él.
La idea es usar Backtracking. Comenzamos desde la fuente dada, exploramos todos los caminos desde el vértice actual. Realizamos un seguimiento de la distancia actual desde la fuente. Si la distancia se vuelve más que k, devolvemos verdadero. Si un camino no produce más de k distancia, retrocedemos.
¿Cómo nos aseguramos de que el camino sea simple y no entremos en un ciclo? La idea es realizar un seguimiento de los vértices de la ruta actual en una array. Cada vez que agregamos un vértice a la ruta, verificamos si ya existe o no en la ruta actual. Si existe, ignoramos el borde.
A continuación se muestra la implementación de la idea anterior.
C++
// Program to find if there is a simple path with
// weight more than k
#include<bits/stdc++.h>
using namespace std;
// iPair ==> Integer Pair
typedef pair<int, int> iPair;
// This class represents a dipathted graph using
// adjacency list representation
class Graph
{
int V; // No. of vertices
// In a weighted graph, we need to store vertex
// and weight pair for every edge
list< pair<int, int> > *adj;
bool pathMoreThanKUtil(int src, int k, vector<bool> &path);
public:
Graph(int V); // Constructor
// function to add an edge to graph
void addEdge(int u, int v, int w);
bool pathMoreThanK(int src, int k);
};
// Returns true if graph has path more than k length
bool Graph::pathMoreThanK(int src, int k)
{
// Create a path array with nothing included
// in path
vector<bool> path(V, false);
// Add source vertex to path
path[src] = 1;
return pathMoreThanKUtil(src, k, path);
}
// Prints shortest paths from src to all other vertices
bool Graph::pathMoreThanKUtil(int src, int k, vector<bool> &path)
{
// If k is 0 or negative, return true;
if (k <= 0)
return true;
// Get all adjacent vertices of source vertex src and
// recursively explore all paths from src.
list<iPair>::iterator i;
for (i = adj[src].begin(); i != adj[src].end(); ++i)
{
// Get adjacent vertex and weight of edge
int v = (*i).first;
int w = (*i).second;
// If vertex v is already there in path, then
// there is a cycle (we ignore this edge)
if (path[v] == true)
continue;
// If weight of is more than k, return true
if (w >= k)
return true;
// Else add this vertex to path
path[v] = true;
// If this adjacent can provide a path longer
// than k, return true.
if (pathMoreThanKUtil(v, k-w, path))
return true;
// Backtrack
path[v] = false;
}
// If no adjacent could produce longer path, return
// false
return false;
}
// Allocates memory for adjacency list
Graph::Graph(int V)
{
this->V = V;
adj = new list<iPair> [V];
}
// Utility function to an edge (u, v) of weight w
void Graph::addEdge(int u, int v, int w)
{
adj[u].push_back(make_pair(v, w));
adj[v].push_back(make_pair(u, w));
}
// Driver program to test methods of graph class
int main()
{
// create the graph given in above figure
int V = 9;
Graph g(V);
// making above shown graph
g.addEdge(0, 1, 4);
g.addEdge(0, 7, 8);
g.addEdge(1, 2, 8);
g.addEdge(1, 7, 11);
g.addEdge(2, 3, 7);
g.addEdge(2, 8, 2);
g.addEdge(2, 5, 4);
g.addEdge(3, 4, 9);
g.addEdge(3, 5, 14);
g.addEdge(4, 5, 10);
g.addEdge(5, 6, 2);
g.addEdge(6, 7, 1);
g.addEdge(6, 8, 6);
g.addEdge(7, 8, 7);
int src = 0;
int k = 62;
g.pathMoreThanK(src, k)? cout << "Yes\n" :
cout << "No\n";
k = 60;
g.pathMoreThanK(src, k)? cout << "Yes\n" :
cout << "No\n";
return 0;
}
Java
// Java Program to find if there is a simple path with
// weight more than k
import java.util.*;
public class GFG{
static class AdjListNode {
int v;
int weight;
AdjListNode(int _v, int _w)
{
v = _v;
weight = _w;
}
int getV() { return v; }
int getWeight() { return weight; }
}
// This class represents a dipathted graph using
// adjacency list representation
static class Graph
{
int V; // No. of vertices
// In a weighted graph, we need to store vertex
// and weight pair for every edge
ArrayList<ArrayList<AdjListNode>> adj;
// Allocates memory for adjacency list
Graph(int V)
{
this.V = V;
adj = new ArrayList<ArrayList<AdjListNode>>(V);
for(int i = 0; i < V; i++)
{
adj.add(new ArrayList<AdjListNode>());
}
}
// Utility function to an edge (u, v) of weight w
void addEdge(int u, int v, int weight)
{
AdjListNode node1 = new AdjListNode(v, weight);
adj.get(u).add(node1); // Add v to u's list
AdjListNode node2 = new AdjListNode(u, weight);
adj.get(v).add(node2); // Add u to v's list
}
// Returns true if graph has path more than k length
boolean pathMoreThanK(int src, int k)
{
// Create a path array with nothing included
// in path
boolean path[] = new boolean[V];
Arrays.fill(path, false);
// Add source vertex to path
path[src] = true;
return pathMoreThanKUtil(src, k, path);
}
// Prints shortest paths from src to all other vertices
boolean pathMoreThanKUtil(int src, int k, boolean[] path)
{
// If k is 0 or negative, return true;
if (k <= 0)
return true;
// Get all adjacent vertices of source vertex src and
// recursively explore all paths from src.
ArrayList<AdjListNode> it = adj.get(src);
int index = 0;
for(int i = 0; i < adj.get(src).size(); i++)
{
AdjListNode vertex = adj.get(src).get(i);
// Get adjacent vertex and weight of edge
int v = vertex.v;
int w = vertex.weight;
// increase theindex
index++;
// If vertex v is already there in path, then
// there is a cycle (we ignore this edge)
if (path[v] == true)
continue;
// If weight of is more than k, return true
if (w >= k)
return true;
// Else add this vertex to path
path[v] = true;
// If this adjacent can provide a path longer
// than k, return true.
if (pathMoreThanKUtil(v, k-w, path))
return true;
// Backtrack
path[v] = false;
}
// If no adjacent could produce longer path, return
// false
return false;
}
}
// Driver program to test methods of graph class
public static void main(String[] args)
{
// create the graph given in above figure
int V = 9;
Graph g = new Graph(V);
// making above shown graph
g.addEdge(0, 1, 4);
g.addEdge(0, 7, 8);
g.addEdge(1, 2, 8);
g.addEdge(1, 7, 11);
g.addEdge(2, 3, 7);
g.addEdge(2, 8, 2);
g.addEdge(2, 5, 4);
g.addEdge(3, 4, 9);
g.addEdge(3, 5, 14);
g.addEdge(4, 5, 10);
g.addEdge(5, 6, 2);
g.addEdge(6, 7, 1);
g.addEdge(6, 8, 6);
g.addEdge(7, 8, 7);
int src = 0;
int k = 62;
if(g.pathMoreThanK(src, k))
System.out.println("YES");
else
System.out.println("NO");
k = 60;
if(g.pathMoreThanK(src, k))
System.out.println("YES");
else
System.out.println("NO");
}
}
// This code is contributed by adityapande88.
Python3
# Program to find if there is a simple path with
# weight more than k
# This class represents a dipathted graph using
# adjacency list representation
class Graph:
# Allocates memory for adjacency list
def __init__(self, V):
self.V = V
self.adj = [[] for i in range(V)]
# Returns true if graph has path more than k length
def pathMoreThanK(self,src, k):
# Create a path array with nothing included
# in path
path = [False]*self.V
# Add source vertex to path
path[src] = 1
return self.pathMoreThanKUtil(src, k, path)
# Prints shortest paths from src to all other vertices
def pathMoreThanKUtil(self,src, k, path):
# If k is 0 or negative, return true
if (k <= 0):
return True
# Get all adjacent vertices of source vertex src and
# recursively explore all paths from src.
i = 0
while i != len(self.adj[src]):
# Get adjacent vertex and weight of edge
v = self.adj[src][i][0]
w = self.adj[src][i][1]
i += 1
# If vertex v is already there in path, then
# there is a cycle (we ignore this edge)
if (path[v] == True):
continue
# If weight of is more than k, return true
if (w >= k):
return True
# Else add this vertex to path
path[v] = True
# If this adjacent can provide a path longer
# than k, return true.
if (self.pathMoreThanKUtil(v, k-w, path)):
return True
# Backtrack
path[v] = False
# If no adjacent could produce longer path, return
# false
return False
# Utility function to an edge (u, v) of weight w
def addEdge(self,u, v, w):
self.adj[u].append([v, w])
self.adj[v].append([u, w])
# Driver program to test methods of graph class
if __name__ == '__main__':
# create the graph given in above figure
V = 9
g = Graph(V)
# making above shown graph
g.addEdge(0, 1, 4)
g.addEdge(0, 7, 8)
g.addEdge(1, 2, 8)
g.addEdge(1, 7, 11)
g.addEdge(2, 3, 7)
g.addEdge(2, 8, 2)
g.addEdge(2, 5, 4)
g.addEdge(3, 4, 9)
g.addEdge(3, 5, 14)
g.addEdge(4, 5, 10)
g.addEdge(5, 6, 2)
g.addEdge(6, 7, 1)
g.addEdge(6, 8, 6)
g.addEdge(7, 8, 7)
src = 0
k = 62
if g.pathMoreThanK(src, k):
print("Yes")
else:
print("No")
k = 60
if g.pathMoreThanK(src, k):
print("Yes")
else:
print("No")
Producción:
No Yes
Ejercicio:
Modifique la solución anterior para encontrar el peso de la ruta más larga desde una fuente dada.
Complejidad de tiempo: O(n!)
Explicación:
Desde el Node de origen, visitamos uno por uno todos los caminos y verificamos si el peso total es mayor que k para cada camino. Entonces, el peor de los casos será cuando el número de caminos posibles sea máximo. Este es el caso cuando cada Node está conectado a todos los demás Nodes.
Comenzando desde el Node de origen, tenemos n-1 Nodes adyacentes. El tiempo necesario para que una ruta conecte dos Nodes cualesquiera es 2. Uno para unir la fuente y el siguiente vértice adyacente. Uno para romper la conexión entre la fuente y el antiguo vértice adyacente.
Después de seleccionar un Node de n-1 Nodes adyacentes, nos quedan n-2 Nodes adyacentes (ya que el Node de origen ya está incluido en la ruta) y así sucesivamente en cada paso de selección de un Node, nuestro problema se reduce en 1 Node.
Podemos escribir esto en forma de relación de recurrencia como: F(n) = n*(2+F(n-1)) Esto se expande a: 2n + 2n*(n-1) + 2n*(n-1 )*(n-2) + ……. + 2n(n-1)(n-2)(n-3)…..1 Como n por 2n(n-1)(n-2)(n-3)….1 es mayor que la expresión dada entonces podemos decir con seguridad que la complejidad del tiempo es: n*2*n! ¡Aquí, en la pregunta, el primer Node se define para que la complejidad del tiempo se convierta en F (n-1) = 2 (n-1) * (n-1)! = 2*n*(n-1)! – 2*1*(n-1)! = 2*n!-2*(n-1)! = O(n!)
Este artículo es una contribución de Shivam Gupta . La explicación de la complejidad del tiempo es aportada por Pranav Nambiar . Escriba comentarios si encuentra algo incorrecto o si desea compartir más información sobre el tema tratado anteriormente.
Publicación traducida automáticamente
Artículo escrito por GeeksforGeeks-1 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA