Dada una array cuadrada, encuentre si es una array Toeplitz o no. Una array de Toeplitz (o constante diagonal) es una array en la que cada diagonal descendente de izquierda a derecha es constante, es decir, todos los elementos de una diagonal son iguales.
En general, cualquier array mat[][] de n×n es una array Toeplitz si cada celda mat[i][j] es igual que mat[i-1][j-1], mat[i+1][j +1], mat[i-2][j-2], mat[i+2][j+2], .. para cada celda mat[i][j] y todas las celdas válidas mat[i+k ][j+k] o mat[ik][jk]
Ejemplos:
Input: mat[N][N] = {{ 6, 7, 8},
{ 4, 6, 7},
{ 1, 4, 6}},
Output : True;
Values in all diagonals are same.
Input: mat[N][N] = {{ 6, 7, 8, 9 },
{ 4, 6, 7, 8 },
{ 1, 4, 6, 7 },
{ 0, 1, 4, 6 }};
Output : True;
Input: mat[N][N] = {{ 6, 3, 8},
{ 4, 9, 7},
{ 1, 4, 6}},
Output : False;
La idea es muy simple. Para cada elemento de la primera fila y la primera columna (o última fila y última columna) en la array, verificamos si la diagonal descendente a partir de ese elemento tiene los mismos valores o no. Si encontramos alguna diagonal con valores diferentes, devolvemos falso.
A continuación se muestra la implementación del código anterior:
C++
// C++ program to check whether given matrix
// is a Toeplitz matrix or not
#include <iostream>
using namespace std;
#define N 5
#define M 4
// Function to check if all elements present in
// descending diagonal starting from position
// (i, j) in the matrix are all same or not
bool checkDiagonal(int mat[N][M], int i, int j)
{
int res = mat[i][j];
while (++i < N && ++j < M)
{
// mismatch found
if (mat[i][j] != res)
return false;
}
// we only reach here when all elements
// in given diagonal are same
return true;
}
// Function to check whether given matrix is a
// Toeplitz matrix or not
bool isToeplitz(int mat[N][M])
{
// do for each element in first row
for (int i = 0; i < M; i++)
{
// check descending diagonal starting from
// position (0, j) in the matrix
if (!checkDiagonal(mat, 0, i))
return false;
}
// do for each element in first column
for (int i = 1; i < N; i++)
{
// check descending diagonal starting from
// position (i, 0) in the matrix
if (!checkDiagonal(mat, i, 0))
return false;
}
// we only reach here when each descending
// diagonal from left to right is same
return true;
}
// Driver code
int main()
{
int mat[N][M] = { { 6, 7, 8, 9 },
{ 4, 6, 7, 8 },
{ 1, 4, 6, 7 },
{ 0, 1, 4, 6 },
{ 2, 0, 1, 4 } };
// Function call
if (isToeplitz(mat))
cout << "Matrix is a Toeplitz ";
else
cout << "Matrix is not a Toeplitz ";
return 0;
}
Java
// Java program to check whether given matrix
// is a Toeplitz matrix or not
import java.io.*;
class GFG
{
public static int N = 5;
public static int M = 4;
// Function to check if all elements present in
// descending diagonal starting from position
// (i, j) in the matrix are all same or not
static boolean checkDiagonal(int mat[][], int i, int j)
{
int res = mat[i][j];
while (++i < N && ++j < M)
{
// mismatch found
if (mat[i][j] != res)
return false;
}
// we only reach here when all elements
// in given diagonal are same
return true;
}
// Function to check whether given matrix is a
// Toeplitz matrix or not
static boolean isToeplitz(int mat[][])
{
// do for each element in first row
for (int i = 0; i < M; i++)
{
// check descending diagonal starting from
// position (0, j) in the matrix
if (!checkDiagonal(mat, 0, i))
return false;
}
// do for each element in first column
for (int i = 1; i < N; i++)
{
// check descending diagonal starting from
// position (i, 0) in the matrix
if (!checkDiagonal(mat, i, 0))
return false;
}
// we only reach here when each descending
// diagonal from left to right is same
return true;
}
// Driver code
public static void main(String[] args)
{
int mat[][] = { { 6, 7, 8, 9 },
{ 4, 6, 7, 8 },
{ 1, 4, 6, 7 },
{ 0, 1, 4, 6 },
{ 2, 0, 1, 4 } };
// Function call
if (isToeplitz(mat))
System.out.println("Matrix is a Toeplitz ");
else
System.out.println("Matrix is not a Toeplitz ");
}
}
// This code is contributed by Pramod Kumar
Python3
# Python3 program to check whether given
# matrix is a Toeplitz matrix or not
N = 5
M = 4
# Function to check if all elements present in
# descending diagonal starting from position
# (i, j) in the matrix are all same or not
def checkDiagonal(mat, i, j):
res = mat[i][j]
i += 1
j += 1
while (i < N and j < M):
# mismatch found
if (mat[i][j] != res):
return False
i += 1
j += 1
# we only reach here when all elements
# in given diagonal are same
return True
# Function to check whether given
# matrix is a Toeplitz matrix or not
def isToeplitz(mat):
# do for each element in first row
for j in range(M):
# check descending diagonal starting from
# position (0, j) in the matrix
if not(checkDiagonal(mat, 0, j)):
return False
# do for each element in first column
for i in range(1, N):
# check descending diagonal starting
# from position (i, 0) in the matrix
if not(checkDiagonal(mat, i, 0)):
return False
return True
# Driver Code
if __name__ == "__main__":
mat = [[6, 7, 8, 9],
[4, 6, 7, 8],
[1, 4, 6, 7],
[0, 1, 4, 6],
[2, 0, 1, 4]]
# Function call
if(isToeplitz(mat)):
print("Matrix is a Toeplitz")
else:
print("Matrix is not a Toeplitz")
# This code is contributed by Jasmine K Grewal
C#
// C# program to check whether given matrix
// is a Toeplitz matrix or not
using System;
class GFG {
public static int N = 5;
public static int M = 4;
// Function to check if all elements present in
// descending diagonal starting from position
// (i, j) in the matrix are all same or not
static bool checkDiagonal(int[, ] mat, int i, int j)
{
int res = mat[i, j];
while (++i < N && ++j < M) {
// mismatch found
if (mat[i, j] != res)
return false;
}
// we only reach here when all elements
// in given diagonal are same
return true;
}
// Function to check whether given matrix is a
// Toeplitz matrix or not
static bool isToeplitz(int[, ] mat)
{
// do for each element in first row
for (int i = 0; i < M; i++) {
// check descending diagonal starting from
// position (0, j) in the matrix
if (!checkDiagonal(mat, 0, i))
return false;
}
// do for each element in first column
for (int i = 1; i < N; i++) {
// check descending diagonal starting from
// position (i, 0) in the matrix
if (!checkDiagonal(mat, i, 0))
return false;
}
// we only reach here when each descending
// diagonal from left to right is same
return true;
}
// Driver code
public static void Main()
{
int[, ] mat = { { 6, 7, 8, 9 },
{ 4, 6, 7, 8 },
{ 1, 4, 6, 7 },
{ 0, 1, 4, 6 },
{ 2, 0, 1, 4 } };
// Function call
if (isToeplitz(mat))
Console.WriteLine("Matrix is a Toeplitz ");
else
Console.WriteLine("Matrix is not a Toeplitz ");
}
}
// This code is contributed by KRV.
PHP
<?php
// PHP program to check whether
// given matrix is a Toeplitz
// matrix or not
// Function to check if all
// elements present in descending
// diagonal starting from position
// (i, j) in the matrix are all
// same or not
function checkDiagonal($mat, $i, $j)
{
$N = 5; $M = 4;
$res = $mat[$i][$j];
while (++$i < $N && ++$j < $M)
{
// mismatch found
if ($mat[$i][$j] != $res)
return false;
}
// we only reach here when
// all elements in given
// diagonal are same
return true;
}
// Function to check whether
// given matrix is a
// Toeplitz matrix or not
function isToeplitz($mat)
{
$N = 5; $M = 4;
// do for each element in first row
for ($i = 0; $i < $M; $i++)
{
// check descending diagonal
// starting from position
// (0, j) in the matrix
if (!checkDiagonal($mat, 0, $i))
return false;
}
// do for each element
// in first column
for ($i = 1; $i < $N; $i++)
{
// check descending diagonal
// starting from position
// (i, 0) in the matrix
if (!checkDiagonal($mat, $i, 0))
return false;
}
// we only reach here when
// each descending diagonal
// from left to right is same
return true;
}
// Driver code
$mat = array(array( 6, 7, 8, 9 ),
array( 4, 6, 7, 8 ),
array( 1, 4, 6, 7 ),
array( 0, 1, 4, 6 ),
array( 2, 0, 1, 4 ));
// Function call
if (isToeplitz($mat))
echo "Matrix is a Toeplitz ";
else
echo "Matrix is not a Toeplitz ";
// This code is contributed
// by nitin mittal.
?>
Javascript
<script>
// Javascript program to check whether given matrix
// is a Toeplitz matrix or not
let N = 5;
let M = 4;
// Function to check if all elements present in
// descending diagonal starting from position
// (i, j) in the matrix are all same or not
function checkDiagonal(mat, i, j)
{
let res = mat[i][j];
while (++i < N && ++j < M)
{
// mismatch found
if (mat[i][j] != res)
return false;
}
// we only reach here when all elements
// in given diagonal are same
return true;
}
// Function to check whether given matrix is a
// Toeplitz matrix or not
function isToeplitz(mat)
{
// do for each element in first row
for (let i = 0; i < M; i++)
{
// check descending diagonal starting from
// position (0, j) in the matrix
if (!checkDiagonal(mat, 0, i))
return false;
}
// do for each element in first column
for (let i = 1; i < N; i++)
{
// check descending diagonal starting from
// position (i, 0) in the matrix
if (!checkDiagonal(mat, i, 0))
return false;
}
// we only reach here when each descending
// diagonal from left to right is same
return true;
}
let mat = [ [ 6, 7, 8, 9 ],
[ 4, 6, 7, 8 ],
[ 1, 4, 6, 7 ],
[ 0, 1, 4, 6 ],
[ 2, 0, 1, 4 ] ];
// Function call
if (isToeplitz(mat))
document.write("Matrix is a Toeplitz ");
else
document.write("Matrix is not a Toeplitz ");
</script>
Matrix is a Toeplitz
La complejidad temporal de esta solución sería O(n 2 ) ya que estamos atravesando cada elemento de la array una sola vez.
Espacio Auxiliar: O(1)
Enfoque basado en hashing:
Considere un elemento en el índice (i, j) de la array de dimensión (m, n). Para que la array sea constante en diagonal, todos los elementos de la diagonal deben ser iguales. Considere la diagonal que contiene este elemento (i, j). Los demás elementos de esta diagonal tendrán su índice de la forma (i+k, j+k) o (ik, jk). Observe que cualquiera que sea el valor de x y el valor de y de estos índices, su diferencia es siempre la misma. es decir (i+k)-(j+k) == (ik)-(jk) == ij.
El siguiente diagrama da una mejor visualización de esta idea. Considere la diagonal de color amarillo. La diferencia entre el valor de x y el valor de y de cualquier índice en esta diagonal es 2 (2-0, 3-1, 4-2, 5-3). Lo mismo se puede observar para todas las diagonales del cuerpo.
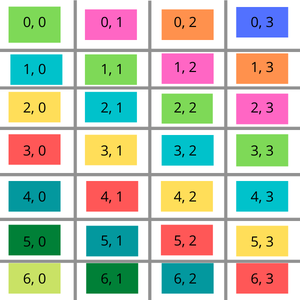
Índice de una array Toeplitz
Para la diagonal de color rojo, la diferencia es 3. Para la diagonal de color verde, la diferencia es 0. Para la diagonal de color naranja, la diferencia es -2 y así sucesivamente…
La idea es explotar el hecho de que para una array de Toeplitz, estas diferencias de índices individuales para diagonales particulares serán únicas. Y dado que es una array de diagonal constante, para todas estas claves únicas, debe haber valores únicos como cualquier elemento en esa diagonal. Entonces, creamos un HashMap para almacenar estos pares (clave, valor). En cualquier momento, si encontramos un valor que es diferente de su correspondiente valor clave almacenado, devolvemos falso.
A continuación se muestra la implementación del código anterior:
C++
// C++ program to check whether given
// matrix is a Toeplitz matrix or not
#include <bits/stdc++.h>
using namespace std;
bool isToeplitz(vector<vector<int>> matrix)
{
// row = number of rows
// col = number of columns
int row = matrix.size();
int col = matrix[0].size();
// HashMap to store key,value pairs
map<int, int> Map;
for(int i = 0; i < row; i++)
{
for(int j = 0; j < col; j++)
{
int key = i - j;
// If key value exists in the hashmap,
if (Map[key])
{
// We check whether the current
// value stored in this key
// matches to element at current
// index or not. If not, return
// false
if (Map[key] != matrix[i][j])
return false;
}
// Else we put key,value pair in hashmap
else
{
Map[i - j] = matrix[i][j];
}
}
}
return true;
}
// Driver code
int main()
{
vector<vector<int>> matrix = { { 12, 23, -32 },
{ -20, 12, 23 },
{ 56, -20, 12 },
{ 38, 56, -20 } };
// Function call
string result = (isToeplitz(matrix)) ? "Yes" : "No";
cout << result;
return 0;
}
// This code is contributed by divyesh072019
Java
// JAVA program to check whether given matrix
// is a Toeplitz matrix or not
import java.util.*;
class GFG {
static boolean isToeplitz(int[][] matrix)
{
// row = number of rows
// col = number of columns
int row = matrix.length;
int col = matrix[0].length;
// HashMap to store key,value pairs
HashMap<Integer, Integer> map
= new HashMap<Integer, Integer>();
for (int i = 0; i < row; i++)
{
for (int j = 0; j < col; j++)
{
int key = i - j;
// if key value exists in the hashmap,
if (map.containsKey(key))
{
// we check whether the current value
// stored in this key matches to element
// at current index or not. If not,
// return false
if (map.get(key) != matrix[i][j])
return false;
}
// else we put key,value pair in hashmap
else {
map.put(i - j, matrix[i][j]);
}
}
}
return true;
}
// Driver Code
public static void main(String[] args)
{
int[][] matrix = { { 12, 23, -32 },
{ -20, 12, 23 },
{ 56, -20, 12 },
{ 38, 56, -20 } };
// Function call
String result = (isToeplitz(matrix)) ? "Yes" : "No";
System.out.println(result);
}
}
Python3
# Python3 program to check whether given matrix
# is a Toeplitz matrix or not
def isToeplitz(matrix):
# row = number of rows
# col = number of columns
row = len(matrix)
col = len(matrix[0])
# dictionary to store key,value pairs
map = {}
for i in range(row):
for j in range(col):
key = i-j
# if key value exists in the map,
if (key in map):
# we check whether the current value stored
# in this key matches to element at current
# index or not. If not, return false
if (map[key] != matrix[i][j]):
return False
# else we put key,value pair in map
else:
map[key] = matrix[i][j]
return True
# Driver Code
if __name__ == "__main__":
matrix = [[12, 23, -32], [-20, 12, 23], [56, -20, 12], [38, 56, -20]]
# Function call
if (isToeplitz(matrix)):
print("Yes")
else:
print("No")
C#
// C# program to check whether given
// matrix is a Toeplitz matrix or not
using System;
using System.Collections.Generic;
class GFG{
static bool isToeplitz(int[,] matrix)
{
// row = number of rows
// col = number of columns
int row = matrix.GetLength(0);
int col = matrix.GetLength(1);
// HashMap to store key,value pairs
Dictionary<int,
int> map = new Dictionary<int,
int>();
for(int i = 0; i < row; i++)
{
for(int j = 0; j < col; j++)
{
int key = i - j;
// If key value exists in the hashmap,
if (map.ContainsKey(key))
{
// We check whether the current value
// stored in this key matches to element
// at current index or not. If not,
// return false
if (map[key] != matrix[i, j])
return false;
}
// Else we put key,value pair in hashmap
else
{
map.Add(i - j, matrix[i, j]);
}
}
}
return true;
}
// Driver code
static void Main()
{
int[,] matrix = { { 12, 23, -32 },
{ -20, 12, 23 },
{ 56, -20, 12 },
{ 38, 56, -20 } };
// Function call
string result = (isToeplitz(matrix)) ?
"Yes" : "No";
Console.WriteLine(result);
}
}
// This code is contributed by divyeshrabadiya07
Javascript
<script>
// JavaScript program to check whether given
// matrix is a Toeplitz matrix or not
function isToeplitz(matrix)
{
// row = number of rows
// col = number of columns
let row = matrix.length;
let col = matrix[0].length;
// HashMap to store key,value pairs
let map = new Map();
for(let i = 0; i < row; i++)
{
for(let j = 0; j < col; j++)
{
let key = i - j;
// If key value exists in the hashmap,
if (map.has(key))
{
// We check whether the current
// value stored in this key
// matches to element at current
// index or not. If not, return
// false
if (map.get(key) != matrix[i][j])
return false;
}
// Else we put key,value pair in hashmap
else
{
map.set(i - j, matrix[i][j]);
}
}
}
return true;
}
// Driver code
let matrix = [ [ 12, 23, -32 ],
[ -20, 12, 23 ],
[ 56, -20, 12 ],
[38, 56, -20 ] ];
// Function call
let result = (isToeplitz(matrix)) ? "Yes" : "No";
document.write(result);
</script>
Yes
Complejidad de tiempo: O(mn) , donde m es el número de filas y n es el número de columnas.
Complejidad espacial: O(m+n) , porque en el peor de los casos, si una array es Toeplitz, tenemos una clave de almacenamiento exactamente (m+n-1), pares de valores. (En la primera fila tenemos n claves distintas y luego para cada m-1 filas, seguimos agregando una clave única al mapa.
Este artículo es una contribución de Aarti_Rathi y Aditya Goel . Si te gusta GeeksforGeeks y te gustaría contribuir, también puedes escribir un artículo usando write.geeksforgeeks.org o enviar tu artículo por correo a review-team@geeksforgeeks.org. Vea su artículo que aparece en la página principal de GeeksforGeeks y ayude a otros Geeks.
Publicación traducida automáticamente
Artículo escrito por GeeksforGeeks-1 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA