Dada una serie de strings, encuentre si las strings dadas se pueden enstringr para formar un círculo. Una string X se puede poner antes de otra string Y en un círculo si el último carácter de X es el mismo que el primer carácter de Y.
Ejemplos:
Input: arr[] = {"geek", "king"}
Output: Yes, the given strings can be chained.
Note that the last character of first string is same
as first character of second string and vice versa is
also true.
Input: arr[] = {"for", "geek", "rig", "kaf"}
Output: Yes, the given strings can be chained.
The strings can be chained as "for", "rig", "geek"
and "kaf"
Input: arr[] = {"aab", "bac", "aaa", "cda"}
Output: Yes, the given strings can be chained.
The strings can be chained as "aaa", "aab", "bac"
and "cda"
Input: arr[] = {"aaa", "bbb", "baa", "aab"};
Output: Yes, the given strings can be chained.
The strings can be chained as "aaa", "aab", "bbb"
and "baa"
Input: arr[] = {"aaa"};
Output: Yes
Input: arr[] = {"aaa", "bbb"};
Output: No
Input : arr[] = ["abc", "efg", "cde", "ghi", "ija"]
Output : Yes
These strings can be reordered as, “abc”, “cde”, “efg”,
“ghi”, “ija”
Input : arr[] = [“ijk”, “kji”, “abc”, “cba”]
Output : No
La idea es crear un gráfico dirigido de todos los caracteres y luego encontrar si hay un circuito euleriano en el gráfico o no.
La representación gráfica de algunas arrays de strings se proporciona en el siguiente diagrama,
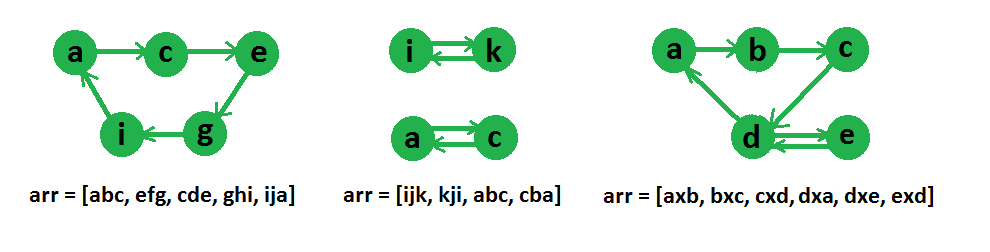
Si hay un circuito euleriano , entonces se puede formar una string, de lo contrario no.
Tenga en cuenta que un gráfico dirigido tiene un circuito euleriano solo si el grado de entrada y salida de cada vértice es el mismo, y todos los vértices de grado distinto de cero forman un solo componente fuertemente conectado.
Los siguientes son pasos detallados del algoritmo.
- Crea un gráfico dirigido g con un número de vértices igual al tamaño del alfabeto. Hemos creado un gráfico con 26 vértices en el siguiente programa.
- Haga lo siguiente para cada string en la array de strings dada.
- …..a) Agregue un borde desde el primer carácter hasta el último carácter del gráfico dado.
- Si el gráfico creado tiene un circuito euleriano , devuelve verdadero, de lo contrario, devuelve falso.
Las siguientes son implementaciones en C++ y Python del algoritmo anterior.
C++
// A C++ program to check if a given
// directed graph is Eulerian or not
#include<iostream>
#include <list>
#define CHARS 26
using namespace std;
// A class that represents an undirected graph
class Graph
{
int V; // No. of vertices
list<int> *adj; // A dynamic array of adjacency lists
int *in;
public:
// Constructor and destructor
Graph(int V);
~Graph() { delete [] adj; delete [] in; }
// function to add an edge to graph
void addEdge(int v, int w) { adj[v].push_back(w); (in[w])++; }
// Method to check if this graph is Eulerian or not
bool isEulerianCycle();
// Method to check if all non-zero degree
// vertices are connected
bool isSC();
// Function to do DFS starting from v. Used in isConnected();
void DFSUtil(int v, bool visited[]);
Graph getTranspose();
};
Graph::Graph(int V)
{
this->V = V;
adj = new list<int>[V];
in = new int[V];
for (int i = 0; i < V; i++)
in[i] = 0;
}
/* This function returns true if the directed
graph has an eulerian cycle, otherwise returns
false */
bool Graph::isEulerianCycle()
{
// Check if all non-zero degree vertices are connected
if (isSC() == false)
return false;
// Check if in degree and out degree
// of every vertex is same
for (int i = 0; i < V; i++)
if (adj[i].size() != in[i])
return false;
return true;
}
// A recursive function to do DFS starting from v
void Graph::DFSUtil(int v, bool visited[])
{
// Mark the current node as visited and print it
visited[v] = true;
// Recur for all the vertices adjacent to this vertex
list<int>::iterator i;
for (i = adj[v].begin(); i != adj[v].end(); ++i)
if (!visited[*i])
DFSUtil(*i, visited);
}
// Function that returns reverse (or transpose) of this graph
// This function is needed in isSC()
Graph Graph::getTranspose()
{
Graph g(V);
for (int v = 0; v < V; v++)
{
// Recur for all the vertices adjacent to this vertex
list<int>::iterator i;
for(i = adj[v].begin(); i != adj[v].end(); ++i)
{
g.adj[*i].push_back(v);
(g.in[v])++;
}
}
return g;
}
// This function returns true if all non-zero
// degree vertices of graph are strongly connected.
// Please refer
// https://www.geeksforgeeks.org/connectivity-in-a-directed-graph/
bool Graph::isSC()
{
// Mark all the vertices as not visited (For first DFS)
bool visited[V];
for (int i = 0; i < V; i++)
visited[i] = false;
// Find the first vertex with non-zero degree
int n;
for (n = 0; n < V; n++)
if (adj[n].size() > 0)
break;
// Do DFS traversal starting from first non zero degree vertex.
DFSUtil(n, visited);
// If DFS traversal doesn’t visit all vertices, then return false.
for (int i = 0; i < V; i++)
if (adj[i].size() > 0 && visited[i] == false)
return false;
// Create a reversed graph
Graph gr = getTranspose();
// Mark all the vertices as not visited (For second DFS)
for (int i = 0; i < V; i++)
visited[i] = false;
// Do DFS for reversed graph starting from first vertex.
// Starting Vertex must be same starting point of first DFS
gr.DFSUtil(n, visited);
// If all vertices are not visited in second DFS, then
// return false
for (int i = 0; i < V; i++)
if (adj[i].size() > 0 && visited[i] == false)
return false;
return true;
}
// This function takes an of strings and returns true
// if the given array of strings can be chained to
// form cycle
bool canBeChained(string arr[], int n)
{
// Create a graph with 'alpha' edges
Graph g(CHARS);
// Create an edge from first character to last character
// of every string
for (int i = 0; i < n; i++)
{
string s = arr[i];
g.addEdge(s[0]-'a', s[s.length()-1]-'a');
}
// The given array of strings can be chained if there
// is an eulerian cycle in the created graph
return g.isEulerianCycle();
}
// Driver program to test above functions
int main()
{
string arr1[] = {"for", "geek", "rig", "kaf"};
int n1 = sizeof(arr1)/sizeof(arr1[0]);
canBeChained(arr1, n1)? cout << "Can be chained \n" :
cout << "Can't be chained \n";
string arr2[] = {"aab", "abb"};
int n2 = sizeof(arr2)/sizeof(arr2[0]);
canBeChained(arr2, n2)? cout << "Can be chained \n" :
cout << "Can't be chained \n";
return 0;
}
Java
// Java program to check if a given
// directed graph is Eulerian or not
import java.util.ArrayList;
import java.util.List;
// A class that represents an
// undirected graph
class GFG{
static final int CHARS = 26;
// No. of vertices
int V;
// A dynamic array of adjacency lists
List<List<Integer>> adj;
int[] in;
// Constructor
GFG(int V)
{
this.V = V;
in = new int[V];
adj = new ArrayList<>(CHARS);
for(int i = 0; i < CHARS; i++)
{
adj.add(i, new ArrayList<>());
}
}
// Function to add an edge to graph
void addEdge(int v, int w)
{
adj.get(v).add(w);
in[w]++;
}
// Method to check if this graph
// is Eulerian or not
boolean isEulerianCycle()
{
// Check if all non-zero degree
// vertices are connected
if (!isSC())
return false;
// Check if in degree and out
// degree of every vertex is same
for(int i = 0; i < V; i++)
if (adj.get(i).size() != in[i])
return false;
return true;
}
// This function returns true if all
// non-zero degree vertices of graph
// are strongly connected. Please refer
boolean isSC()
{
// Mark all the vertices as not
// visited (For first DFS)
boolean[] visited = new boolean[V];
for(int i = 0; i < V; i++)
visited[i] = false;
// Find the first vertex with
// non-zero degree
int n;
for(n = 0; n < V; n++)
if (adj.get(n).size() > 0)
break;
// Do DFS traversal starting from
// first non zero degree vertex.
DFSUtil(n, visited);
// If DFS traversal doesn't visit all
// vertices, then return false.
for(int i = 0; i < V; i++)
if (adj.get(i).size() > 0 && !visited[i])
return false;
// Create a reversed graph
GFG gr = getTranspose();
// Mark all the vertices as not
// visited (For second DFS)
for(int i = 0; i < V; i++)
visited[i] = false;
// Do DFS for reversed graph starting
// from first vertex. Starting Vertex
// must be same starting point of first DFS
gr.DFSUtil(n, visited);
// If all vertices are not visited in
// second DFS, then return false
for(int i = 0; i < V; i++)
if (adj.get(i).size() > 0 && !visited[i])
return false;
return true;
}
// Function to do DFS starting from v.
// Used in isConnected();
// A recursive function to do DFS
// starting from v
void DFSUtil(int v, boolean[] visited)
{
// Mark the current node as
// visited and print it
visited[v] = true;
// Recur for all the vertices
// adjacent to this vertex
for(Integer i : adj.get(v))
if (!visited[i])
{
DFSUtil(i, visited);
}
}
// Function that returns reverse
// (or transpose) of this graph
// This function is needed in isSC()
GFG getTranspose()
{
GFG g = new GFG(V);
for(int v = 0; v < V; v++)
{
// Recur for all the vertices
// adjacent to this vertex
for(Integer i : adj.get(v))
{
g.adj.get(i).add(v);
g.in[v]++;
}
}
return g;
}
// This function takes an of strings
// and returns true if the given array
// of strings can be chained to form cycle
static boolean canBeChained(String[] arr, int n)
{
// Create a graph with 'alpha' edges
GFG g = new GFG(CHARS);
// Create an edge from first character
// to last character of every string
for(int i = 0; i < n; i++)
{
String s = arr[i];
g.addEdge(s.charAt(0) - 'a',
s.charAt(s.length() - 1) - 'a');
}
// The given array of strings can be
// chained if there is an eulerian
// cycle in the created graph
return g.isEulerianCycle();
}
// Driver code
public static void main(String[] args) throws Exception
{
String[] arr1 = { "for", "geek",
"rig", "kaf" };
int n1 = arr1.length;
System.out.println((canBeChained(arr1, n1) ?
"Can be chained " :
"Can't be chained "));
String[] arr2 = { "aab", "abb" };
int n2 = arr2.length;
System.out.println((canBeChained(arr2, n2) ?
"Can be chained " :
"Can't be chained "));
}
}
// This code is contributed by abhay379201
Python3
# Python program to check if a given directed graph is Eulerian or not
CHARS = 26
# A class that represents an undirected graph
class Graph(object):
def __init__(self, V):
self.V = V # No. of vertices
self.adj = [[] for x in range(V)] # a dynamic array
self.inp = [0] * V
# function to add an edge to graph
def addEdge(self, v, w):
self.adj[v].append(w)
self.inp[w]+=1
# Method to check if this graph is Eulerian or not
def isSC(self):
# Mark all the vertices as not visited (For first DFS)
visited = [False] * self.V
# Find the first vertex with non-zero degree
n = 0
for n in range(self.V):
if len(self.adj[n]) > 0:
break
# Do DFS traversal starting from first non zero degree vertex.
self.DFSUtil(n, visited)
# If DFS traversal doesn't visit all vertices, then return false.
for i in range(self.V):
if len(self.adj[i]) > 0 and visited[i] == False:
return False
# Create a reversed graph
gr = self.getTranspose()
# Mark all the vertices as not visited (For second DFS)
for i in range(self.V):
visited[i] = False
# Do DFS for reversed graph starting from first vertex.
# Starting Vertex must be same starting point of first DFS
gr.DFSUtil(n, visited)
# If all vertices are not visited in second DFS, then
# return false
for i in range(self.V):
if len(self.adj[i]) > 0 and visited[i] == False:
return False
return True
# This function returns true if the directed graph has an eulerian
# cycle, otherwise returns false
def isEulerianCycle(self):
# Check if all non-zero degree vertices are connected
if self.isSC() == False:
return False
# Check if in degree and out degree of every vertex is same
for i in range(self.V):
if len(self.adj[i]) != self.inp[i]:
return False
return True
# A recursive function to do DFS starting from v
def DFSUtil(self, v, visited):
# Mark the current node as visited and print it
visited[v] = True
# Recur for all the vertices adjacent to this vertex
for i in range(len(self.adj[v])):
if not visited[self.adj[v][i]]:
self.DFSUtil(self.adj[v][i], visited)
# Function that returns reverse (or transpose) of this graph
# This function is needed in isSC()
def getTranspose(self):
g = Graph(self.V)
for v in range(self.V):
# Recur for all the vertices adjacent to this vertex
for i in range(len(self.adj[v])):
g.adj[self.adj[v][i]].append(v)
g.inp[v]+=1
return g
# This function takes an of strings and returns true
# if the given array of strings can be chained to
# form cycle
def canBeChained(arr, n):
# Create a graph with 'alpha' edges
g = Graph(CHARS)
# Create an edge from first character to last character
# of every string
for i in range(n):
s = arr[i]
g.addEdge(ord(s[0])-ord('a'), ord(s[len(s)-1])-ord('a'))
# The given array of strings can be chained if there
# is an eulerian cycle in the created graph
return g.isEulerianCycle()
# Driver program
arr1 = ["for", "geek", "rig", "kaf"]
n1 = len(arr1)
if canBeChained(arr1, n1):
print ("Can be chained")
else:
print ("Cant be chained")
arr2 = ["aab", "abb"]
n2 = len(arr2)
if canBeChained(arr2, n2):
print ("Can be chained")
else:
print ("Can't be chained")
# This code is contributed by BHAVYA JAIN
Can be chained Can't be chained
Encuentra si una array de strings se puede enstringr para formar un círculo | conjunto 2
Publicación traducida automáticamente
Artículo escrito por GeeksforGeeks-1 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA