Encuentre todos los Nodes accesibles de cada Node presente en un conjunto dado

Dado un gráfico no dirigido y un conjunto de vértices, encuentre todos los Nodes accesibles desde cada vértice presente en el conjunto dado.

Considere el siguiente gráfico no dirigido con 2 componentes desconectados. 

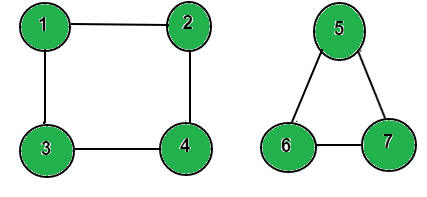
arr[] = {1 , 2 , 5}
Reachable nodes from 1 are  1, 2, 3, 4
Reachable nodes from 2 are 1, 2, 3, 4
Reachable nodes from 5 are 5, 6, 7

Método 1 (Simple) 

Una solución sencilla es hacer un recorrido BFS para cada Node presente en el conjunto y luego encontrar todos los Nodes accesibles. 

Suponga que necesitamos encontrar Nodes alcanzables para n Nodes, la complejidad de tiempo para esta solución sería O(n*(V+E)) donde V es el número de Nodes en el gráfico y E es el número de aristas en el gráfico.

Tenga en cuenta que debemos llamar a BFS como una llamada separada para cada Node sin usar la array visitada de recorridos anteriores porque es posible que sea necesario imprimir un mismo vértice varias veces. Esta parece ser una solución efectiva, pero considere el caso cuando E = Θ(V ² ) y n = V, la complejidad del tiempo se convierte en O(V ³ ).

Método 2 (eficiente) 

Dado que el gráfico dado no está dirigido, todos los vértices que pertenecen al mismo componente tienen el mismo conjunto de Nodes accesibles. Así que hacemos un seguimiento de las asignaciones de vértices y componentes. A cada componente del gráfico se le asigna un número y a cada vértice de este componente se le asigna este número. Usamos la array de visitas para este propósito, la array que se usa para realizar un seguimiento de los vértices visitados en BFS. 

For a node u, 
if visit[u] is 0 then
    u has not been visited before
else // if not zero then
   visit[u] represents the component number. 

For any two nodes u and v belonging to same 
component, visit[u] is equal to visit[v]

Para almacenar los Nodes accesibles, use un mapa m con clave como número de componente y valor como vector que almacena todos los Nodes accesibles. 

Para encontrar Nodes accesibles para un Node, devuelva m[visit[u]] Mire el pseudocódigo a continuación para comprender cómo asignar números de componentes.  

componentNum = 0
for i=1 to n    
    If visit[i] is NOT 0 then
        componentNum++ 
         
        // bfs() returns a list (or vector)
        // for given vertex 'i'
        list = bfs(i, componentNum)
        m[visit[i]]] = list

Para el gráfico que se muestra en el ejemplo, la array de visitas sería. 

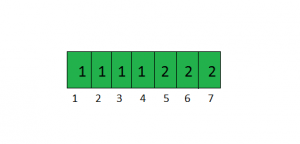
Para los Nodes 1, 2, 3 y 4 el número de componente es 1. Para los Nodes 5, 6 y 7 el número de componente es 2.

Implementación de la idea anterior

// C++ program to find all the reachable nodes
// for every node present in arr[0..n-1].
#include <bits/stdc++.h>
using namespace std;
 
// This class represents a directed graph using
// adjacency list representation
class Graph
{
public:
    int V;    // No. of vertices
 
    // Pointer to an array containing adjacency lists
    list<int> *adj;
 
    Graph(int );  // Constructor
 
    void addEdge(int, int);
 
    vector<int> BFS(int, int, int []);
};
 
Graph::Graph(int V)
{
    this->V = V;
    adj = new list<int>[V+1];
}
 
void Graph::addEdge(int u, int v)
{
    adj[u].push_back(v); // Add w to v’s list.
    adj[v].push_back(u); // Add v to w’s list.
}
 
vector<int> Graph::BFS(int componentNum, int src,
                                    int visited[])
{
    // Mark all the vertices as not visited
    // Create a queue for BFS
    queue<int> queue;
 
    queue.push(src);
 
    // Assign Component Number
    visited[src] = componentNum;
 
    // Vector to store all the reachable nodes from 'src'
    vector<int> reachableNodes;
 
    while(!queue.empty())
    {
        // Dequeue a vertex from queue
        int u = queue.front();
        queue.pop();
 
        reachableNodes.push_back(u);
 
        // Get all adjacent vertices of the dequeued
        // vertex u. If a adjacent has not been visited,
        // then mark it visited and enqueue it
        for (auto itr = adj[u].begin();
                itr != adj[u].end(); itr++)
        {
            if (!visited[*itr])
            {
                // Assign Component Number to all the
                // reachable nodes
                visited[*itr] = componentNum;
                queue.push(*itr);
            }
        }
    }
    return reachableNodes;
}
 
// Display all the Reachable Nodes from a node 'n'
void displayReachableNodes(int n,
            unordered_map <int, vector<int> > m)
{
    vector<int> temp = m[n];
    for (int i=0; i<temp.size(); i++)
        cout << temp[i] << " ";
 
    cout << endl;
}
 
// Find all the reachable nodes for every element
// in the arr
void findReachableNodes(Graph g, int arr[], int n)
{
    // Get the number of nodes in the graph
    int V = g.V;
 
    // Take a integer visited array and initialize
    // all the elements with 0
    int visited[V+1];
    memset(visited, 0, sizeof(visited));
 
    // Map to store list of reachable Nodes for a
    // given node.
    unordered_map <int, vector<int> > m;
 
    // Initialize component Number with 0
    int componentNum = 0;
 
    // For each node in arr[] find reachable
    // Nodes
    for (int i = 0 ; i < n ; i++)
    {
        int u = arr[i];
 
        // Visit all the nodes of the component
        if (!visited[u])
        {
            componentNum++;
 
            // Store the reachable Nodes corresponding to
            // the node 'i'
            m[visited[u]] = g.BFS(componentNum, u, visited);
        }
 
        // At this point, we have all reachable nodes
        // from u, print them by doing a look up in map m.
        cout << "Reachable Nodes from " << u <<" are\n";
        displayReachableNodes(visited[u], m);
    }
}
 
// Driver program to test above functions
int main()
{
    // Create a graph given in the above diagram
    int V = 7;
    Graph g(V);
    g.addEdge(1, 2);
    g.addEdge(2, 3);
    g.addEdge(3, 4);
    g.addEdge(3, 1);
    g.addEdge(5, 6);
    g.addEdge(5, 7);
 
    // For every ith element in the arr
    // find all reachable nodes from query[i]
    int arr[] = {2, 4, 5};
 
    // Find number of elements in Set
    int n = sizeof(arr)/sizeof(int);
 
    findReachableNodes(g, arr, n);
 
    return 0;
}

# Python3 program to find all the reachable nodes
# for every node present in arr[0..n-1]
from collections import deque
 
def addEdge(v, w):
     
    global visited, adj
    adj[v].append(w)
    adj[w].append(v)
 
def BFS(componentNum, src):
     
    global visited, adj
     
    # Mark all the vertices as not visited
    # Create a queue for BFS
    #a =  visited
    queue = deque()
 
    queue.append(src)
 
    # Assign Component Number
    visited[src] = 1
 
    # Vector to store all the reachable
    # nodes from 'src'
    reachableNodes = []
    #print("0:",visited)
 
    while (len(queue) > 0):
         
        # Dequeue a vertex from queue
        u = queue.popleft()
 
        reachableNodes.append(u)
 
        # Get all adjacent vertices of the dequeued
        # vertex u. If a adjacent has not been visited,
        # then mark it visited and enqueue it
        for itr in adj[u]:
            if (visited[itr] == 0):
                 
                # Assign Component Number to all the
                # reachable nodes
                visited[itr] = 1
                queue.append(itr)
 
    return reachableNodes
 
# Display all the Reachable Nodes
# from a node 'n'
def displayReachableNodes(m):
     
    for i in m:
        print(i, end = " ")
 
    print()
 
def findReachableNodes(arr, n):
     
    global V, adj, visited
     
    # Get the number of nodes in the graph
 
    # Map to store list of reachable Nodes for a
    # given node.
    a = []
 
    # Initialize component Number with 0
    componentNum = 0
 
    # For each node in arr[] find reachable
    # Nodes
    for i in range(n):
        u = arr[i]
 
        # Visit all the nodes of the component
        if (visited[u] == 0):
            componentNum += 1
 
            # Store the reachable Nodes corresponding
            # to the node 'i'
            a = BFS(componentNum, u)
 
        # At this point, we have all reachable nodes
        # from u, print them by doing a look up in map m.
        print("Reachable Nodes from ", u, " are")
        displayReachableNodes(a)
 
# Driver code
if __name__ == '__main__':
     
    V = 7
    adj = [[] for i in range(V + 1)]
    visited = [0 for i in range(V + 1)]
    addEdge(1, 2)
    addEdge(2, 3)
    addEdge(3, 4)
    addEdge(3, 1)
    addEdge(5, 6)
    addEdge(5, 7)
 
    # For every ith element in the arr
    # find all reachable nodes from query[i]
    arr = [ 2, 4, 5 ]
 
    # Find number of elements in Set
    n = len(arr)
 
    findReachableNodes(arr, n)
 
# This code is contributed by mohit kumar 29

Reachable Nodes from 2 are
2 1 3 4 
Reachable Nodes from 4 are
2 1 3 4 
Reachable Nodes from 5 are
5 6 7 

Análisis de Complejidad de Tiempo: 

n = Tamaño del conjunto dado 
E = Número de aristas 
V = Número de Nodes 
O(V+E) para BFS 
En el peor de los casos, todos los Nodes V se muestran para cada Node presente en el dado, es decir, solo un componente en el gráfico, por lo que toma tiempo O(n*V).

Complejidad temporal en el peor de los casos: O(V+E) + O(n*V)

Este artículo es una contribución de Chirag Agarwal . Si te gusta GeeksforGeeks y te gustaría contribuir, también puedes escribir un artículo usando write.geeksforgeeks.org o enviar tu artículo por correo a review-team@geeksforgeeks.org. Vea su artículo que aparece en la página principal de GeeksforGeeks y ayude a otros Geeks.