Representemos ![]() el par ordenado del segundo máximo y el máximo elemento de un arreglo respectivamente. Necesitamos encontrar todos esos pares únicos en subarreglos contiguos generales de un arreglo dado.
el par ordenado del segundo máximo y el máximo elemento de un arreglo respectivamente. Necesitamos encontrar todos esos pares únicos en subarreglos contiguos generales de un arreglo dado.
Ejemplos:
Entrada: Arr = [ 1, 2, 3, 4, 5 ]
Salida: (1, 2) (2, 3) (3, 4) (4, 5)Entrada: Arr = [ 1, 1, 2 ]
Salida: (1, 1) (1, 2)Entrada: Arr = [ 1, 2, 6, 4, 5 ]
Salida: (1, 2) (2, 6) (4, 5) (4, 6) (5, 6)
Enfoque de fuerza bruta :
- Una forma sencilla de resolver este problema sería escanear cada subarreglo y encontrar el máximo y el segundo elemento máximo en ese subarreglo.
- Esto se puede hacer en el
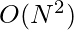 tiempo
tiempo - Luego, podemos insertar cada par en un conjunto para garantizar que se eliminen los duplicados y luego imprimirlos
- Cada operación de inserción cuesta
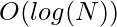 , empujando la complejidad final a
, empujando la complejidad final a 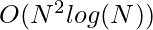
C++14
// C++ implementation
#include <bits/stdc++.h>
using namespace std;
// Function to return the set of pairs
set<pair<int, int> > pairs(vector<int>& arr)
{
set<pair<int, int> > pairs;
// find all subarrays
for (int i = 0; i < arr.size() - 1; ++i) {
int maximum = max(arr[i], arr[i + 1]),
secondmax = min(arr[i], arr[i + 1]);
for (int j = i + 1; j < arr.size(); ++j) {
// update max and second max
if (arr[j] > maximum) {
secondmax = maximum;
maximum = arr[j];
}
if (arr[j] < maximum && arr[j] > secondmax) {
secondmax = arr[j];
}
// insert a pair in set
pairs.insert(make_pair(secondmax, maximum));
}
}
return pairs;
}
int main()
{
vector<int> vec = { 1, 2, 6, 4, 5 };
set<pair<int, int> > st = pairs(vec);
cout << "Total Number of valid pairs is :"
<< (int)st.size() << "\n";
for (auto& x : st) {
cout << "(" << x.first << ", " << x.second << ") ";
}
return 0;
}
Java
// Java implementation
import java.util.HashSet;
import java.util.Set;
class Pair implements Comparable<Pair> {
int first, second;
public Pair(int first, int second)
{
this.first = first;
this.second = second;
}
@Override public int hashCode()
{
return 31 * first + second;
}
public boolean equals(Object p)
{
Pair pair = (Pair)p;
if (this.first != pair.first)
return false;
return this.second == pair.second;
}
@Override public int compareTo(Pair p)
{
if (this.first == p.first) {
return this.second - p.second;
}
return this.first - p.first;
}
}
class GFG {
// Function to return the set of pairs
static Set<Pair> pairs(int[] arr)
{
Set<Pair> pairs = new HashSet<>();
// Find all subarrays
for (int i = 0; i < arr.length - 1; ++i) {
int maximum = Math.max(arr[i], arr[i + 1]),
secondmax = Math.min(arr[i], arr[i + 1]);
for (int j = i + 1; j < arr.length; ++j) {
// Update max and second max
if (arr[j] > maximum) {
secondmax = maximum;
maximum = arr[j];
}
if (arr[j] < maximum
&& arr[j] > secondmax) {
secondmax = arr[j];
}
// Insert a pair in set
pairs.add(new Pair(secondmax, maximum));
}
}
return pairs;
}
// Driver Code
public static void main(String[] args)
{
int[] vec = { 1, 2, 6, 4, 5 };
Set<Pair> st = pairs(vec);
System.out.println("Total Number of "
+ "valid pairs is :"
+ st.size());
for (Pair x : st) {
System.out.printf("(%d, %d)\n", x.first,
x.second);
}
}
}
// This code is contributed by sanjeev2552
Python3
# python3 implementation
# Function to return the set of pairs
def SetofPairs(arr):
pairs = set()
n = len(arr) # length of array
# find all subarrays
for i in range(n - 1):
maximum = max(arr[i], arr[i + 1])
secondmax = min(arr[i], arr[i + 1])
for j in range(i + 1, n):
# update max and second max
if (arr[j] > maximum):
secondmax = maximum
maximum = arr[j]
if (arr[j] < maximum and arr[j] > secondmax):
secondmax = arr[j]
# add a pair in set
pairs.add((secondmax, maximum))
return pairs
# Driver code
if __name__ == "__main__":
vec = [1, 2, 6, 4, 5]
st = SetofPairs(vec)
print("Total Number of valid pairs is :", len(st))
for x in st:
print(x, end = " ")
# This code is contributed by sunilsoni10220001022000.
Javascript
<script>
// JavaScript implementation
// Function to return the set of pairs
function pairs(arr)
{
var pairs = new Set();
// find all subarrays
for (var i = 0; i < arr.length - 1; ++i) {
var maximum = Math.max(arr[i], arr[i + 1]),
secondmax = Math.min(arr[i], arr[i + 1]);
for (var j = i + 1; j < arr.length; ++j) {
// update max and second max
if (arr[j] > maximum) {
secondmax = maximum;
maximum = arr[j];
}
if (arr[j] < maximum && arr[j] > secondmax) {
secondmax = arr[j];
}
// insert a pair in set
pairs.add([secondmax, maximum].toString());
}
}
return pairs;
}
var vec = [1, 2, 6, 4, 5 ];
var st = pairs(vec);
document.write( "Total Number of valid pairs is :" +
st.size + "<br>");
[...st].sort().forEach(x => {
x = x.split(',');
document.write( "(" + x[0] + ", " + x[1] + ") ")
})
</script>
Producción:
Total Number of valid pairs is :5 (1, 2) (2, 6) (4, 5) (4, 6) (5, 6)
Análisis de Complejidad:
- Complejidad de tiempo: O(N^2 log(N)).
La inserción en el set toma log N tiempo. Puede haber como máximo N^2 subarreglos. Entonces, la complejidad del tiempo es O (N ^ 2 log N). - Espacio Auxiliar: O(n^2).
Como se requiere espacio adicional para almacenar los elementos en un conjunto.
Enfoque eficiente :
- Podría reducir la complejidad de encontrar pares al
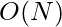 observar que un elemento
observar que un elemento 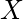 puede formar pares con elementos solo hasta el elemento más cercano a la derecha que es mayor que
puede formar pares con elementos solo hasta el elemento más cercano a la derecha que es mayor que 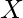 .
. - Para ver por qué esto se cumple, considere
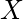 =
= 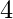 en el siguiente ejemplo.
en el siguiente ejemplo.
Arr = {1, 4, 5, 3, 2, 1}
- Pudo ver que
 es el elemento más cercano a la derecha que es mayor que
es el elemento más cercano a la derecha que es mayor que 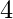 .
. 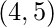 forma un par considerando el subarreglo
forma un par considerando el subarreglo ![Rendered by QuickLaTeX.com [4, 5]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-82e833014a06179fc9ccaec4f7410ad8_l3.png) .
. - Otros subarreglos, que comienzan con
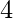 must include
must include 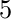 . Considerando uno de ellos, si
. Considerando uno de ellos, si 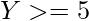 existe otro elemento en el subconjunto, entonces
existe otro elemento en el subconjunto, entonces 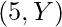 será el par para ese subconjunto.
será el par para ese subconjunto. - De lo contrario
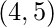 , se formará o
, se formará o 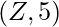 se formará, donde
se formará, donde 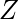 está el elemento máximo a la derecha del
está el elemento máximo a la derecha del 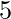 subarreglo.
subarreglo. - En cualquier caso,
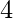 no puede formar pareja con ningún elemento a la derecha de
no puede formar pareja con ningún elemento a la derecha de 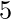 .
. - Usando esta observación, podemos implementar la lógica usando la pila que reduce la complejidad de generación de pares a
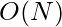 .
. - Cada par se puede insertar en un conjunto para eliminar duplicados, dando una complejidad de tiempo final de
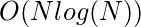
A continuación se muestra la implementación del enfoque anterior:
C++
// C++ implementation of the above approach
#include <bits/stdc++.h>
using namespace std;
// Function to return the set of pairs
set<pair<int, int>>
pairs(vector<int>& arr)
{
stack<int> st;
set<pair<int, int>> pairs;
// Push first element into stack
st.push(arr[0]);
// For each element 'X' in arr,
// pop the stack while top Element
// is smaller than 'X' and form a pair.
// If the stack is not empty after
// the previous operation, create
// a pair. Push X into the stack.
for (int i = 1; i < arr.size(); ++i) {
while (!st.empty() &&
arr[i] > st.top()) {
pairs.insert(make_pair(st.top(),
arr[i]));
st.pop();
}
if (!st.empty()) {
pairs.insert(make_pair(min(st.top(),
arr[i]),
max(st.top(),
arr[i])));
}
st.push(arr[i]);
}
return pairs;
}
int main()
{
vector<int> vec = { 1, 2, 6, 4, 5 };
set<pair<int, int> > st = pairs(vec);
cout << "Total Number of valid pairs is :"
<< (int)st.size() << "\n";
for (auto& x : st) {
cout << "(" << x.first << ", "
<< x.second << ") ";
}
return 0;
}
Java
// Java implementation of the above approach
import java.util.*;
class GFG{
static class pair
{
int first, second;
public pair(int first, int second)
{
this.first = first;
this.second = second;
}
@Override
public int hashCode()
{
final int prime = 31;
int result = 1;
result = prime * result + first;
result = prime * result + second;
return result;
}
@Override
public boolean equals(Object obj)
{
if (this == obj)
return true;
if (obj == null)
return false;
if (getClass() != obj.getClass())
return false;
pair other = (pair) obj;
if (first != other.first)
return false;
if (second != other.second)
return false;
return true;
}
}
// Function to return the set of pairs
static HashSet<pair> pairs(int[] arr)
{
Stack<Integer> st = new Stack<Integer>();
HashSet<pair> pairs = new HashSet<pair>();
// Push first element into stack
st.add(arr[0]);
// For each element 'X' in arr,
// pop the stack while top Element
// is smaller than 'X' and form a pair.
// If the stack is not empty after
// the previous operation, create
// a pair. Push X into the stack.
for(int i = 1; i < arr.length; ++i)
{
while (!st.isEmpty() && arr[i] > st.peek())
{
pairs.add(new pair(st.peek(),
arr[i]));
st.pop();
}
if (!st.isEmpty())
{
pairs.add(new pair(Math.min(st.peek(),
arr[i]),
Math.max(st.peek(),
arr[i])));
}
st.add(arr[i]);
}
return pairs;
}
// Driver code
public static void main(String[] args)
{
int [] vec = { 1, 2, 6, 4, 5 };
HashSet<pair> st = pairs(vec);
System.out.print("Total Number of valid pairs is :" +
(int)st.size() + "\n");
for(pair x : st)
{
System.out.print("(" + x.first+ ", " +
x.second + ") ");
}
}
}
// This code is contributed by 29AjayKumar
Python3
# Python3 implementation of the above approach
# Function to return the set of pairs
def pairs(arr) :
st = [];
pairs = [];
# Push first element into stack
st.append(arr[0]);
# For each element 'X' in arr,
# pop the stack while top Element
# is smaller than 'X' and form a pair.
# If the stack is not empty after
# the previous operation, create
# a pair. Push X into the stack.
for i in range(1, len(arr) ) :
while len(st) != 0 and arr[i] > st[-1] :
pairs.append((st[-1], arr[i]));
st.pop();
if len(st) != 0 :
pairs.append((min(st[-1], arr[i]),
max(st[-1], arr[i])));
st.append(arr[i]);
return pairs;
# Driver code
if __name__ == "__main__" :
vec = [ 1, 2, 6, 4, 5 ];
st = pairs(vec);
print("Total Number of valid pairs is :",len(st));
for x in st :
print("(" ,x[0], ", ",x[1], ")",end=" ");
# This code is contributed by AnkitRai01
Producción:
Total Number of valid pairs is :5 (1, 2) (2, 6) (4, 5) (4, 6) (5, 6)
Análisis de Complejidad:
- Complejidad temporal: O(N log(N)).
Cada par se puede insertar en un conjunto para eliminar duplicados, dando una complejidad de tiempo final de O (N log N) - Espacio Auxiliar: O(N).
Como se requiere espacio adicional para almacenar los elementos en un conjunto.
Publicación traducida automáticamente
Artículo escrito por ankurdubey521 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA