Dada una array de números enteros, debe encontrar tres números tales que la suma de dos elementos sea igual al tercer elemento.
Ejemplos:
Input : {5, 32, 1, 7, 10, 50, 19, 21, 2}
Output : 21, 2, 19
Input : {5, 32, 1, 7, 10, 50, 19, 21, 0}
Output : no such triplet exist
Fuente de la pregunta: experiencia de entrevista con Arcesium | Conjunto 7 (En el campus para prácticas)
Enfoque simple: ejecute tres bucles y verifique si existe un triplete tal que la suma de dos elementos sea igual al tercer elemento.
Complejidad del tiempo: O(n^3)
Enfoque eficiente: la idea es similar a encontrar un triplete que sume un valor dado.
- Primero ordene la array dada.
- Comience a fijar el mayor elemento de tres desde atrás y recorra la array para encontrar los otros dos números que suman el tercer elemento.
- Tome dos punteros j (desde el frente) y k (inicialmente i-1) para encontrar el menor de los dos números y desde i-1 para encontrar el mayor de los dos números restantes
- Si la suma de ambos números sigue siendo menor que A[i], entonces necesitamos aumentar el valor de la suma de dos números, aumentando así el puntero j, para aumentar el valor de A[j] + A[ k] .
- Si la suma de ambos números es mayor que A[i], entonces debemos disminuir el valor de la suma de dos números, por lo tanto, disminuir el puntero k para disminuir el valor total de A[j] + A[k ] .
La imagen de abajo es una ejecución en seco del enfoque anterior:
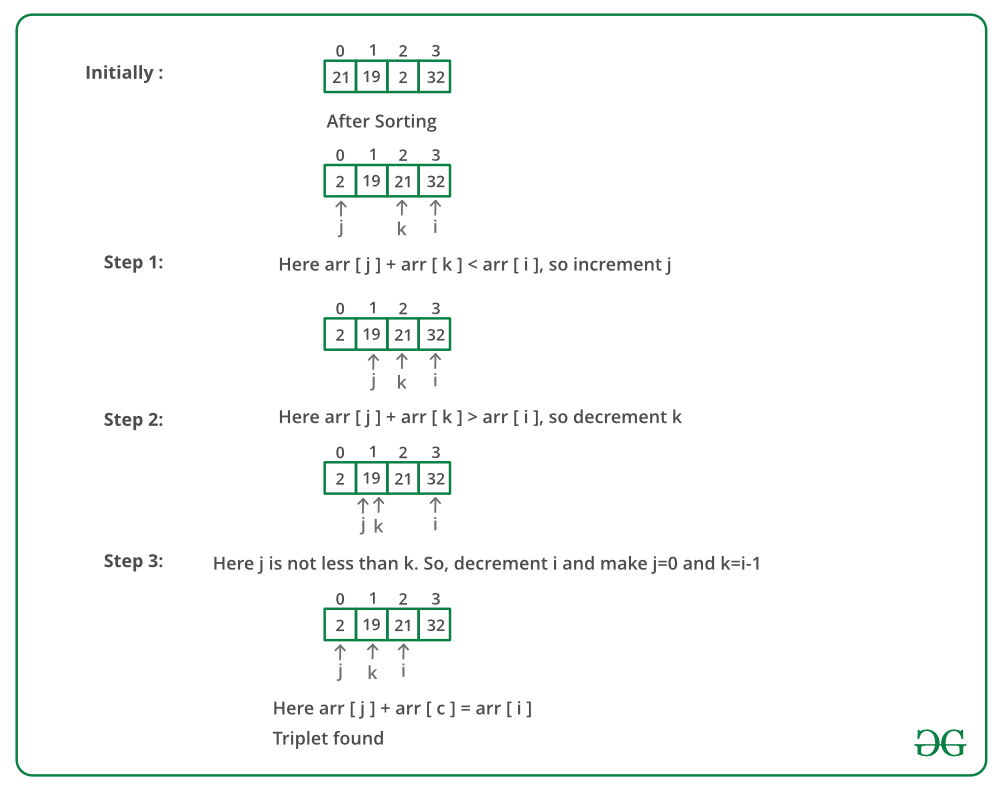
A continuación se muestra la implementación del enfoque anterior:
C++
// CPP program to find three numbers
// such that sum of two makes the
// third element in array
#include <bits/stdc++.h>
using namespace std;
// Utility function for finding
// triplet in array
void findTriplet(int arr[], int n)
{
// sort the array
sort(arr, arr + n);
// for every element in arr
// check if a pair exist(in array) whose
// sum is equal to arr element
for (int i = n - 1; i >= 0; i--) {
int j = 0;
int k = i - 1;
// Iterate forward and backward to find
// the other two elements
while (j < k) {
// If the two elements sum is
// equal to the third element
if (arr[i] == arr[j] + arr[k]) {
// pair found
cout << "numbers are " << arr[i] << " "
<< arr[j] << " " << arr[k] << endl;
return;
}
// If the element is greater than
// sum of both the elements, then try
// adding a smaller number to reach the
// equality
else if (arr[i] > arr[j] + arr[k])
j += 1;
// If the element is smaller, then
// try with a smaller number
// to reach equality, so decrease K
else
k -= 1;
}
}
// No such triplet is found in array
cout << "No such triplet exists";
}
// driver program
int main()
{
int arr[] = { 5, 32, 1, 7, 10, 50, 19, 21, 2 };
int n = sizeof(arr) / sizeof(arr[0]);
findTriplet(arr, n);
return 0;
}
Java
// Java program to find three numbers
// such that sum of two makes the
// third element in array
import java.util.Arrays;
public class GFG {
// utility function for finding
// triplet in array
static void findTriplet(int arr[], int n)
{
// sort the array
Arrays.sort(arr);
// for every element in arr
// check if a pair exist(in array) whose
// sum is equal to arr element
for (int i = n - 1; i >= 0; i--) {
int j = 0;
int k = i - 1;
while (j < k) {
if (arr[i] == arr[j] + arr[k]) {
// pair found
System.out.println("numbers are " + arr[i] + " "
+ arr[j] + " " + arr[k]);
return;
}
else if (arr[i] > arr[j] + arr[k])
j += 1;
else
k -= 1;
}
}
// no such triplet is found in array
System.out.println("No such triplet exists");
}
// driver program
public static void main(String args[])
{
int arr[] = { 5, 32, 1, 7, 10, 50, 19, 21, 2 };
int n = arr.length;
findTriplet(arr, n);
}
}
// This code is contributed by Sumit Ghosh
Python
# Python program to find three numbers # such that sum of two makes the # third element in array # utility function for finding # triplet in array def findTriplet(arr, n): # sort the array arr.sort() # for every element in arr # check if a pair exist(in array) whose # sum is equal to arr element i = n - 1 while(i >= 0): j = 0 k = i - 1 while (j < k): if (arr[i] == arr[j] + arr[k]): # pair found print "numbers are ", arr[i], arr[j], arr[k] return elif (arr[i] > arr[j] + arr[k]): j += 1 else: k -= 1 i -= 1 # no such triplet is found in array print "No such triplet exists" # driver program arr = [ 5, 32, 1, 7, 10, 50, 19, 21, 2 ] n = len(arr) findTriplet(arr, n) # This code is contributed by Sachin Bisht
C#
// C# program to find three numbers
// such that sum of two makes the
// third element in array
using System;
public class GFG {
// utility function for finding
// triplet in array
static void findTriplet(int[] arr, int n)
{
// sort the array
Array.Sort(arr);
// for every element in arr
// check if a pair exist(in
// array) whose sum is equal
// to arr element
for (int i = n - 1; i >= 0; i--) {
int j = 0;
int k = i - 1;
while (j < k) {
if (arr[i] == arr[j] + arr[k]) {
// pair found
Console.WriteLine("numbers are "
+ arr[i] + " " + arr[j]
+ " " + arr[k]);
return;
}
else if (arr[i] > arr[j] + arr[k])
j += 1;
else
k -= 1;
}
}
// no such triplet is found in array
Console.WriteLine("No such triplet exists");
}
// driver program
public static void Main()
{
int[] arr = { 5, 32, 1, 7, 10, 50,
19, 21, 2 };
int n = arr.Length;
findTriplet(arr, n);
}
}
// This code is contributed by vt_m.
PHP
<?php
// PHP program to find three
// numbers such that sum of
// two makes the third
// element in array
// utility function for
// finding triplet in array
function findTriplet($arr, $n)
{
// sort the array
sort($arr);
// for every element in
// arr check if a pair
// exist(in array) whose
// sum is equal to arr element
for ($i = $n - 1; $i >= 0; $i--)
{
$j = 0;
$k = $i - 1;
while ($j < $k)
{
if ($arr[$i] == $arr[$j] + $arr[$k])
{
// pair found
echo "numbers are ", $arr[$i], " ",
$arr[$j], " ",
$arr[$k];
return;
}
else if ($arr[$i] > $arr[$j] +
$arr[$k])
$j += 1;
else
$k -= 1;
}
}
// no such triplet
// is found in array
echo "No such triplet exists";
}
// Driver Code
$arr = array(5, 32, 1, 7, 10,
50, 19, 21, 2 );
$n = count($arr);
findTriplet($arr, $n);
// This code is contributed by anuj_67.
?>
Javascript
<script>
// Javascript program to find three numbers
// such that sum of two makes the
// third element in array
// Utility function for finding
// triplet in array
function findTriplet(arr, n)
{
// sort the array
arr.sort((a,b) => a-b);
// for every element in arr
// check if a pair exist(in array) whose
// sum is equal to arr element
for (let i = n - 1; i >= 0; i--) {
let j = 0;
let k = i - 1;
// Iterate forward and backward to find
// the other two elements
while (j < k) {
// If the two elements sum is
// equal to the third element
if (arr[i] == arr[j] + arr[k]) {
// pair found
document.write("numbers are " + arr[i] +
" " + arr[j] + " " + arr[k] + "<br>");
return;
}
// If the element is greater than
// sum of both the elements, then try
// adding a smaller number to reach the
// equality
else if (arr[i] > arr[j] + arr[k])
j += 1;
// If the element is smaller, then
// try with a smaller number
// to reach equality, so decrease K
else
k -= 1;
}
}
// No such triplet is found in array
document.write("No such triplet exists");
}
// driver program
let arr = [ 5, 32, 1, 7, 10, 50, 19, 21, 2 ];
let n = arr.length;
findTriplet(arr, n);
// This code is contributed by Mayank Tyagi
</script>
numbers are 21 2 19
Complejidad del tiempo: O(N^2)
Otro enfoque: la idea es similar al enfoque anterior:
- Ordenar la array dada.
- Inicie un bucle anidado, fijando el primer elemento i (de 0 a n-1) y moviendo el otro j (de i+1 a n-1).
- Tome la suma de ambos elementos y búsquelo en la array restante usando la búsqueda binaria.
Implementación:
C++
// CPP program to find three numbers
// such that sum of two makes the
// third element in array
#include <bits/stdc++.h>
#include <iostream>
using namespace std;
// function to perform binary search
bool search(int sum, int start, int end, int arr[])
{
while (start <= end) {
int mid = (start + end) / 2;
if (arr[mid] == sum) {
return true;
}
else if (arr[mid] > sum) {
end = mid - 1;
}
else {
start = mid + 1;
}
}
return false;
}
// function to find the triplets
void findTriplet(int arr[], int n)
{
// sorting the array
sort(arr, arr + n);
// initialising nested loops
for (int i = 0; i < n; i++) {
for (int j = i + 1; j < n; j++) {
// finding the sum of the numbers
if (search((arr[i] + arr[j]), j, n - 1, arr)) {
// printing out the first triplet
cout << "Numbers are: " << arr[i] << " "
<< arr[j] << " " << (arr[i] + arr[j]);
return;
}
}
}
// if no such triplets are found
cout << "No such numbers exist" << endl;
}
int main()
{
int arr[] = { 5, 32, 1, 7, 10, 50, 19, 21, 2 };
int n = sizeof(arr) / sizeof(arr[0]);
findTriplet(arr, n);
return 0;
}
// This code is contributed by Sarthak Delori
Java
// Java program to find three numbers
// such that sum of two makes the
// third element in array
import java.util.*;
class GFG{
// Function to perform binary search
static boolean search(int sum, int start,
int end, int arr[])
{
while (start <= end)
{
int mid = (start + end) / 2;
if (arr[mid] == sum)
{
return true;
}
else if (arr[mid] > sum)
{
end = mid - 1;
}
else
{
start = mid + 1;
}
}
return false;
}
// Function to find the triplets
static void findTriplet(int arr[], int n)
{
// Sorting the array
Arrays.sort(arr);
// Initialising nested loops
for(int i = 0; i < n; i++)
{
for(int j = i + 1; j < n; j++)
{
// Finding the sum of the numbers
if (search((arr[i] + arr[j]), j, n - 1, arr))
{
// Printing out the first triplet
System.out.print("Numbers are: " + arr[i] + " " +
arr[j] + " " + (arr[i] + arr[j]));
return;
}
}
}
// If no such triplets are found
System.out.print("No such numbers exist");
}
// Driver code
public static void main(String args[])
{
int arr[] = { 5, 32, 1, 7, 10, 50, 19, 21, 2 };
int n = arr.length;
findTriplet(arr, n);
}
}
// This code is contributed by target_2
Python3
# Python program to find three numbers
# such that sum of two makes the
# third element in array
from functools import cmp_to_key
def mycmp(a, b):
return a - b
def search(sum, start, end, arr):
while (start <= end):
mid = (start + end) // 2
if (arr[mid] == sum):
return True
elif (arr[mid] > sum):
end = mid - 1
else:
start = mid + 1
return False
# Utility function for finding
# triplet in array
def findTriplet(arr, n):
# sort the array
arr.sort(key = cmp_to_key(mycmp))
# initialising nested loops
for i in range(n):
for j in range(i + 1,n):
if (search((arr[i] + arr[j]), j, n - 1, arr)):
print(f"numbers are {arr[i]} {arr[j]} {( arr[i] + arr[j] )}")
return
# No such triplet is found in array
print("No such triplet exists")
# driver program
arr = [ 5, 32, 1, 7, 10, 50, 19, 21, 2 ]
n = len(arr)
findTriplet(arr, n)
# This code is contributed by shinjanpatra
C#
// C# program to find three numbers
// such that sum of two makes the
// third element in array
using System;
public class GFG {
// function to perform binary search
static bool search(int sum, int start, int end, int [] arr)
{
while (start <= end) {
int mid = (start + end) / 2;
if (arr[mid] == sum) {
return true;
}
else if (arr[mid] > sum) {
end = mid - 1;
}
else {
start = mid + 1;
}
}
return false;
}
// utility function for finding
// triplet in array
static void findTriplet(int[] arr, int n)
{
// sort the array
Array.Sort(arr);
// for every element in arr
// check if a pair exist(in
// array) whose sum is equal
// to arr element
for (int i = 0; i < n; i++) {
for(int j=i+1;j<n;j++)
{
// finding the sum of the numbers
if (search((arr[i] + arr[j]), j, n - 1, arr)) {
// pair found
Console.WriteLine("Numbers are "
+ arr[i] + " " + arr[j]
+ " " + (arr[i]+arr[j]));
return;
}
}
}
// no such triplet is found in array
Console.WriteLine("No such triplet exists");
}
// driver program
public static void Main()
{
int[] arr = { 5, 32, 1, 7, 10, 50,
19, 21, 2 };
int n = arr.Length;
findTriplet(arr, n);
}
}
// This code is contributed by Aarti_Rathi
Javascript
<script>
// Javascript program to find three numbers
// such that sum of two makes the
// third element in array
bool search(sum, start, end, arr)
{
while (start <= end) {
let mid = (start + end) / 2;
if (arr[mid] == sum) {
return true;
}
else if (arr[mid] > sum) {
end = mid - 1;
}
else {
start = mid + 1;
}
}
return false;
}
// Utility function for finding
// triplet in array
function findTriplet(arr, n)
{
// sort the array
arr.sort((a,b) => a-b);
// initialising nested loops
for (let i = 0; i < n; i++) {
for (let j = i + 1; j < n; j++) {
if (search((arr[i] + arr[j]), j, n - 1, arr)) {
document.write("numbers are " + arr[i] +
" " + arr[j] + " " + ( arr[i] + arr[j] ) + "<br>");
}
}
}
// No such triplet is found in array
document.write("No such triplet exists");
}
// driver program
let arr = [ 5, 32, 1, 7, 10, 50, 19, 21, 2 ];
let n = arr.length;
findTriplet(arr, n);
// This code is contributed by Sarthak Delori
</script>
Numbers are: 2 5 7
Complejidad de tiempo: O(N^2*log N)
Complejidad de espacio: O(1)
Este artículo es una contribución de Mandeep Singh . Si te gusta GeeksforGeeks y te gustaría contribuir, también puedes escribir un artículo usando write.geeksforgeeks.org o enviar tu artículo por correo a review-team@geeksforgeeks.org. Vea su artículo que aparece en la página principal de GeeksforGeeks y ayude a otros Geeks.
Publicación traducida automáticamente
Artículo escrito por GeeksforGeeks-1 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA