Dado un conjunto de puntos, conecta los puntos sin cruzarlos.


Ejemplo:
Input: points[] = {(0, 3), (1, 1), (2, 2), (4, 4),
(0, 0), (1, 2), (3, 1}, {3, 3}};
Output: Connecting points in following order would
not cause any crossing
{(0, 0), (3, 1), (1, 1), (2, 2), (3, 3),
(4, 4), (1, 2), (0, 3)}
Le recomendamos encarecidamente que minimice su navegador y que pruebe esto usted mismo primero.
La idea es utilizar la clasificación.
- Encuentre el punto más bajo comparando la coordenada y de todos los puntos. Si hay dos puntos con el mismo valor de y, entonces se considera el punto con menor valor de coordenada x. Coloque el punto más inferior en la primera posición.
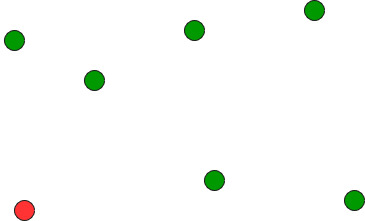
- Considere los n-1 puntos restantes y ordénelos por ángulo polor en sentido contrario a las agujas del reloj alrededor de los puntos [0]. Si el ángulo polor de dos puntos es el mismo, coloque primero el punto más cercano.
- Atravesar la array ordenada (ordenada en orden creciente de ángulo) produce una ruta cerrada simple.

¿Cómo calcular ángulos?
Una solución es usar funciones trigonométricas.
Observación: No nos importan los valores reales de los ángulos. Solo queremos ordenar por ángulo.
Idea: ¡Usa la orientación para comparar ángulos sin calcularlos realmente!
A continuación se muestra la implementación en C++ de la idea anterior.
C++
// A C++ program to find simple closed path for n points
// for explanation of orientation()
#include <bits/stdc++.h>
using namespace std;
struct Point
{
int x, y;
};
// A global point needed for sorting points with reference
// to the first point. Used in compare function of qsort()
Point p0;
// A utility function to swap two points
int swap(Point &p1, Point &p2)
{
Point temp = p1;
p1 = p2;
p2 = temp;
}
// A utility function to return square of distance between
// p1 and p2
int dist(Point p1, Point p2)
{
return (p1.x - p2.x)*(p1.x - p2.x) +
(p1.y - p2.y)*(p1.y - p2.y);
}
// To find orientation of ordered triplet (p, q, r).
// The function returns following values
// 0 --> p, q and r are collinear
// 1 --> Clockwise
// 2 --> Counterclockwise
int orientation(Point p, Point q, Point r)
{
int val = (q.y - p.y) * (r.x - q.x) -
(q.x - p.x) * (r.y - q.y);
if (val == 0) return 0; // collinear
return (val > 0)? 1: 2; // clockwise or counterclock wise
}
// A function used by library function qsort() to sort
// an array of points with respect to the first point
int compare(const void *vp1, const void *vp2)
{
Point *p1 = (Point *)vp1;
Point *p2 = (Point *)vp2;
// Find orientation
int o = orientation(p0, *p1, *p2);
if (o == 0)
return (dist(p0, *p2) >= dist(p0, *p1))? -1 : 1;
return (o == 2)? -1: 1;
}
// Prints simple closed path for a set of n points.
void printClosedPath(Point points[], int n)
{
// Find the bottommost point
int ymin = points[0].y, min = 0;
for (int i = 1; i < n; i++)
{
int y = points[i].y;
// Pick the bottom-most. In case of tie, chose the
// left most point
if ((y < ymin) || (ymin == y &&
points[i].x < points[min].x))
ymin = points[i].y, min = i;
}
// Place the bottom-most point at first position
swap(points[0], points[min]);
// Sort n-1 points with respect to the first point.
// A point p1 comes before p2 in sorted output if p2
// has larger polar angle (in counterclockwise
// direction) than p1
p0 = points[0];
qsort(&points[1], n-1, sizeof(Point), compare);
// Now stack has the output points, print contents
// of stack
for (int i=0; i<n; i++)
cout << "(" << points[i].x << ", "
<< points[i].y <<"), ";
}
// Driver program to test above functions
int main()
{
Point points[] = {{0, 3}, {1, 1}, {2, 2}, {4, 4},
{0, 0}, {1, 2}, {3, 1}, {3, 3}};
int n = sizeof(points)/sizeof(points[0]);
printClosedPath(points, n);
return 0;
}
Producción:
(0, 0), (3, 1), (1, 1), (2, 2), (3, 3), (4, 4), (1, 2), (0, 3),
La complejidad temporal de la solución anterior es O(n Log n) si usamos un algoritmo de clasificación O(nLogn) para clasificar los puntos.
Espacio Auxiliar: O(1), ya que no se ha ocupado ningún espacio extra.
Fuente:
http://www.dcs.gla.ac.uk/~pat/52233/slides/Geometry1x1.pdf
Este artículo es una contribución de Aarti_Rathi y Rajeev Agrawal . Escriba comentarios si encuentra algo incorrecto o si desea compartir más información sobre el tema tratado anteriormente.
Publicación traducida automáticamente
Artículo escrito por GeeksforGeeks-1 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA