Encuentre valores mínimos y máximos entre todos los Nodes hoja máximos de todos los posibles Binary Max Heap

Dado un entero positivo N , la tarea es encontrar los elementos más grandes y más pequeños, a partir de los Nodes de hoja máximos de cada montón máximo binario posible formado al tomar los primeros N números naturales como el valor de los Nodes del montón máximo binario.

Ejemplos:

Entrada: N = 2
Salida: 1 1
Explicación: 
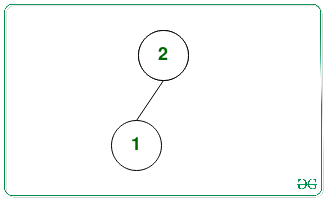
Solo hay un montón binario máximo con los Nodes {1, 2}:  

En el árbol anterior, el valor máximo del Node hoja = 1.
Por lo tanto, el elemento más grande es 1 y el elemento más pequeño también es 1.

Entrada: N = 3
Salida: 2 2
Explicación: 
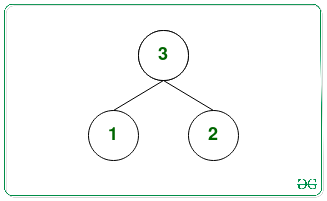
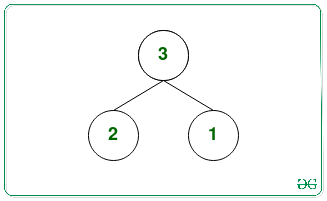
Hay dos montones binarios máximos posibles con los Nodes {1, 2, 3}:

Los Nodes hoja máximos del primer y segundo montón son 2 y 2 respectivamente.  
Por lo tanto, el elemento más grande es 2 y el elemento más pequeño también es 2.

Enfoque ingenuo: el enfoque más simple es generar todos los montones binarios máximos posibles que se pueden formar a partir de los primeros N números naturales y realizar un seguimiento de los valores de Node de hoja más pequeños y más grandes entre todos los Nodes de hoja máximos en todos los montones. 

Complejidad temporal: O(N*N!)
Espacio auxiliar: O(1)

Enfoque eficiente: el enfoque anterior se puede optimizar en función de las siguientes observaciones:

1. El montón máximo es un árbol binario completo , por lo tanto, la altura y el número de Nodes hoja son fijos.
2. En el montón máximo, el valor del Node siempre es mayor o igual que los hijos de ese Node.
3. El valor máximo del Node hoja siempre es mayor o igual que el número de hojas del árbol. Por lo tanto, el valor máximo de un Node hoja se minimizará si los números más pequeños se colocan en los Nodes hoja. Y será igual al número de hojas del Node.
4. Una propiedad más de los montones máximos es que, a medida que uno baja en el árbol, los valores de los Nodes disminuyen. Por lo tanto, el valor máximo de un Node se maximizará si se coloca un número en el Node hoja con la menor profundidad posible. Entonces, si D es la profundidad de ese Node, el valor máximo posible del Node será igual a ND.
5. Si D es la profundidad del montón máximo, las posibles profundidades de los Nodes hoja son D y D-1 únicamente, ya que los montones son el árbol binario completo.
6. Si V es un Node hoja, entonces (2*V) debe ser mayor que N . Por lo tanto, el recuento de Nodes hoja es igual a (N – N/2).

Siga los pasos a continuación para resolver el problema:

• Calcule el recuento de Nodes hoja en el montón máximo de N Nodes , como se explicó anteriormente, y guárdelo en una variable, por ejemplo, numberOfleaves .

numberOfleaves = (N- N/2).

• Encuentre la profundidad del montón máximo y guárdelo en una variable, digamos D .

D = ceil(log2(N+1))-1

• Si N+1 no es una potencia de 2 y D es mayor que 1 , entonces debe salir un Node hoja en la profundidad D-1 . Por lo tanto, disminuya D en 1.
• Finalmente, después de completar los pasos anteriores, imprima el valor más grande como (ND) y el valor más pequeño como numberOfleaves .

A continuación se muestra la implementación del enfoque anterior:

// C++ program for the above approach
#include <bits/stdc++.h>
using namespace std;
 
// Function to find largest and smallest
// elements from the maximum leaf nodes
// values from all possible binary max heap
void leafNodeValues(int N)
{
    // Stores count of leaf nodes
    int numberOfLeaves = (N - N / 2);
 
    // Stores minDepth with N
    int minDepth = ceil(log2(N + 1)) - 1;
 
    // Increment N by 1
    N++;
    // If N is not power of 2 and minDepth
    // is greater than 1
    if (minDepth > 1 && (N & (N - 1)))
        minDepth--;
 
    // Print the smallest and largest possible
    // value of a leaf node
    cout << numberOfLeaves << ' '
         << N - minDepth - 1;
}
 
// Driver Code
int main()
{
    // Given Input
    int N = 2;
 
    // Function Call
    leafNodeValues(N);
 
    return 0;
}

// Java program for the above approach
class GFG{
     
// Function to find largest and smallest
// elements from the maximum leaf nodes
// values from all possible binary max heap
static void leafNodeValues(int N)
{
     
    // Stores count of leaf nodes
    int numberOfLeaves = (N - N / 2);
  
    // Stores minDepth with N
    int minDepth = (int)Math.ceil(Math.log(N + 1) /
                                  Math.log(2)) - 1;
  
    // Increment N by 1
    N++;
     
    // If N is not power of 2 and minDepth
    // is greater than 1
    if (minDepth > 1 && (N & (N - 1)) != 0)
        minDepth--;
  
    // Print the smallest and largest possible
    // value of a leaf node
    System.out.println(numberOfLeaves + " " +
                      (N - minDepth - 1));
}
 
// Driver code
public static void main(String[] args)
{
     
    // Given Input
    int N = 2;
  
    // Function Call
    leafNodeValues(N);
}
}
 
// This code is contributed by divyesh072019

# Python 3 program for the above approach
from math import ceil,log2
 
# Function to find largest and smallest
# elements from the maximum leaf nodes
# values from all possible binary max heap
def leafNodeValues(N):
   
    # Stores count of leaf nodes
    numberOfLeaves = (N - N // 2)
 
    # Stores minDepth with N
    minDepth = ceil(log2(N + 1)) - 1;
 
    # Increment N by 1
    N += 1
     
    # If N is not power of 2 and minDepth
    # is greater than 1
    if (minDepth > 1 and (N & (N - 1))):
        minDepth -= 1
 
    # Print the smallest and largest possible
    # value of a leaf node
    print(numberOfLeaves, N - minDepth - 1)
 
# Driver Code
if __name__ == '__main__':
    # Given Input
    N = 2
     
    # Function Call
    leafNodeValues(N)
     
    # This code is contributed by SURENDRA_GANGWAR.

// C# program for the above approach
using System;
class GFG {
     
    // Function to find largest and smallest
    // elements from the maximum leaf nodes
    // values from all possible binary max heap
    static void leafNodeValues(int N)
    {
          
        // Stores count of leaf nodes
        int numberOfLeaves = (N - N / 2);
       
        // Stores minDepth with N
        int minDepth = (int)Math.Ceiling(Math.Log(N + 1) /
                                      Math.Log(2)) - 1;
       
        // Increment N by 1
        N++;
          
        // If N is not power of 2 and minDepth
        // is greater than 1
        if (minDepth > 1 && (N & (N - 1)) != 0)
            minDepth--;
       
        // Print the smallest and largest possible
        // value of a leaf node
        Console.WriteLine(numberOfLeaves + " " +
                          (N - minDepth - 1));
    }
 
  static void Main()
  {
     
    // Given Input
    int N = 2;
   
    // Function Call
    leafNodeValues(N);
  }
}
 
// This code is contributed by decode2207.

<script>
  
// JavaScript program for the above approach
 
// Function to find largest and smallest
// elements from the maximum leaf nodes
// values from all possible binary max heap
function log2(n)
 {
   return (Math.log(n)/Math.log(2));
 }
function leafNodeValues(N)
{
    // Stores count of leaf nodes
    let numberOfLeaves = parseInt((N - N / 2));
 
    // Stores minDepth with N
    let minDepth = Math.ceil(log2(N + 1)) - 1;
 
    // Increment N by 1
    N++;
    // If N is not power of 2 and minDepth
    // is greater than 1
    if ((minDepth > 1) && (N & (N - 1)))
        minDepth--;
 
    // Print the smallest and largest possible
    // value of a leaf node
    document.write(numberOfLeaves);
    document.write(' ');
    document.write( N - minDepth - 1);
}
 
// Driver Code
 
    // Given Input
    var N = 2;
 
    // Function Call
    leafNodeValues(N);
     
// This code is contributed by Potta Lokesh
   
</script>

1 1

Complejidad de tiempo: O(log(N))
Espacio auxiliar: O(1)