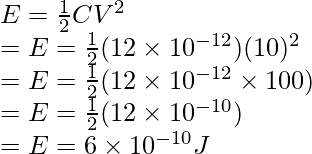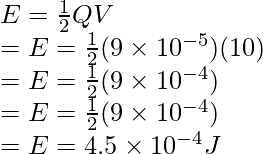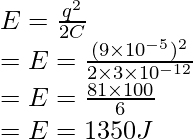Energía almacenada en un condensador

Los condensadores se utilizan en casi todos los dispositivos electrónicos que nos rodean. Desde un ventilador hasta un chip, hay muchos capacitores de diferentes tamaños a nuestro alrededor. Teóricamente, la función básica del capacitor es almacenar energía. Su uso común incluye almacenamiento de energía, protección contra picos de voltaje y filtrado de señales. Fue inventado por un científico alemán, Ewald Georg von Kleist, en 1745. Físicamente, un capacitor son solo dos conductores separados por un aislante. Son capaces de mantener una carga que da lugar a muchas de sus propiedades. Estudiemos estas propiedades en detalle.

Condensadores y Capacitancia

Un condensador es un sistema de dos cargas que están separadas por un aislante. Digamos que los dos conductores tienen una carga de Q ₁ y Q ₂ y un potencial V ₁ y V _2. Por lo general, las cargas son Q y -Q. El campo eléctrico en esta región es proporcional a la carga en la superficie de los capacitores. La siguiente figura muestra dos conductores con cargas Q y -Q en ellos. Estos conductores están separados por un aislante.

Ahora se sabe que el potencial no es más que el trabajo realizado para llevar la carga desde el infinito hasta la posición actual. De esta manera, el potencial también se vuelve proporcional a la carga de los conductores. Esto significa que la relación de carga y potencial es constante. La relación se denomina capacitancia.

$C = \frac{Q}{V}$

Aunque cualquier forma y tamaño sirven para hacer un capacitor, en la vida real la mayoría de estos capacitores son cilíndricos. Al hacer cálculos y para el símbolo, el capacitor se denota como un capacitor de placas paralelas.

Condensador de placas paralelas

Un condensador de placas paralelas consta de dos grandes planos paralelos separados por una pequeña distancia. La mayoría de las veces, el medio entre las placas se considera vacío, pero puede ser cualquier material aislante. La figura muestra el diagrama de un capacitor de placas paralelas que está conectado a una batería.

Energía almacenada en un condensador

Cuando una batería se conecta a través de las placas de un condensador, la corriente carga el condensador, lo que lleva a la acumulación de cargas en las placas opuestas. A medida que se acumulan las cargas, la diferencia de potencial entre las placas comienza a aumentar. Digamos que la capacitancia del capacitor es «C», inicialmente estaba descargado. Ahora, después de estar conectado a la batería, digamos que hay una diferencia de potencial, «V» que se desarrolla entre las placas. Considere «q» como la carga en las placas en ese momento. Después,

q = CV

El trabajo realizado para llevar la carga desde el infinito al potencial de «V» está dado por,

W = qV

Suponga que la batería entrega una carga de «dq» a las placas mientras mantiene el potencial constante. Después,

W = dq.V = $\frac{q}{C}dq$

De esta manera, se transfiere una carga total “q” de la batería al capacitor. Entonces, el trabajo realizado estará dado por

$W = \int \frac{q}{C}dq = \frac{q^2}{2C}$

Entonces, la energía almacenada en el capacitor es,

$E = \frac{q^2}{2C}$

Usando la relación anterior, q = CV

La energía se puede reescribir como,

$E= \frac{C^2V^2}{2C}\\E=\frac{1}{2}CV^2$

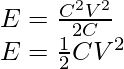
Usando la relación, C= q/V

La energía se puede escribir como,

$E= \frac{1}{2}CV^2\\E= \frac{1}{2}\frac{q}{V}V^2\\E=\frac{1}{2}qV^2$

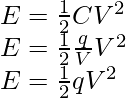
Por lo tanto, las tres fórmulas obtenidas para Energía almacenada en un capacitor ,

$E = \frac{q^2}{2C} = \frac{1}{2}CV^2 = \frac{1}{2}qV$

Problemas de muestra

Pregunta 1: Encuentre la capacitancia si se mantiene una carga de 3C y un potencial de 9V en las placas.

Solución:

La relación para la capacitancia está dada por,

q = CV

Dado: q = 3C y V = 9V

q = CV

⇒ 3 = C(9)

⇒ $\frac{1}{3}$ = C

C = 0.333F

Pregunta 2: Encuentre la capacitancia si se mantiene una carga de 18C y un potencial de 3V entre las placas.

Solución:

La relación para la capacitancia está dada por,

q = CV

Dado: q = 18C y V = 3V

q = CV

⇒ 18 = C(3)

⇒ 6 = C

C = 6F

Pregunta 3: Encuentre la capacitancia si se mantiene una carga de 1C y un potencial de 2V entre placas.

Solución:

La relación para la capacitancia está dada por,

q = CV

Dado: q = 1C y V = 2V

q = CV

⇒ 1 = C(2)

⇒ 0.5 = C

C = 0.5F

Pregunta 4: Encuentra la energía almacenada en el capacitor de 12pF que está conectado a una batería de 10V.

Solución:

La relación para la energía almacenada en un capacitor está dada por,

$E = \frac{1}{2}CV^2$

Dado: C = 12pF y V = 10V

$E = \frac{1}{2}CV^2 \\ = E = \frac{1}{2}(12 \times 10^{-12})(10)^2 \\ = E = \frac{ 1}{2}(12 \times 10^{-12} \times 100) \\ = E = \frac{1}{2}(12 \times 10^{-10}) \\ = E = 6 \ veces 10^{-10} J$

Pregunta 5: Encuentra la energía almacenada en el capacitor que tiene una carga de 9 x 10 ^-5 C y está conectado a una batería de 10V.

Solución:

La relación para la energía almacenada en un capacitor está dada por,

$E = \frac{1}{2}QV$

Dado: q = 9 x 10 ^-5 y V = 10V

$E = \frac{1}{2}QV \\ = E = \frac{1}{2}(9 \times 10^{-5})(10) \\ = E = \frac{1}{2 }(9 \times 10^{-4})\\ = E = \frac{1}{2}(9 \times 10^{-4}) \\ = E = 4,5 \times 10^{-4} j$

Pregunta 6: Encuentra la energía almacenada en el capacitor de 3pF que tiene una carga de 9 x 10 ^-5 C.

Solución:

La relación para la energía almacenada en un capacitor está dada por,

$mi = \frac{q^2}{2C}$

Dado: q = 9 x 10 ^-5 y C = 3 x 10 ^-12

$E = \frac{q^2}{2C} \\ = E = \frac{(9 \times 10^{-5})^2}{2 \times 3 \times 10^{-12}} \\ = E = \frac{81 \times 100}{6} \\ = E = 1350 J$

Pregunta 7: Un capacitor de capacitancia “C”, primero se conecta a una batería de voltaje V y se carga completamente, luego se conecta a una batería de voltaje 2V. Encuentre la energía electrostática ganada/perdida en este proceso.

Solución:

Primero, el capacitor se conecta a una batería de potencial V.

Energía del condensador después de la carga completa,

mi ₁ = $\frac{1}{2}CV^2$

Después de conectarla a otra batería,

mi ₂ = $\frac{1}{2}C(2V)^2$

⇒E2 = _{_} $\frac{1}{2}4CV^2$

Cambio de energía en este proceso = E _{2 –} E ₁

= $\frac{1}{2}4CV^2 - \frac{1}{2}CV^2$

= $\frac{3}{2}CV^2$

Ya que, el cambio de energía es positivo. En el proceso se ganó energía electrostática.