Todos y cada uno de los objetos poseen energía. En un movimiento armónico simple, el objeto va al extremo y adquiere energía potencial. Cuando el objeto vuelve a la posición media, su velocidad es máxima. Así, en este caso, el potencial se convierte en energía cinética y viceversa. En un movimiento armónico simple ideal, la energía se conserva. Aunque puede cambiar de forma, la energía total permanece constante. Es fundamental estudiar estos cambios de energía y la energía total para analizar el MAS y sus propiedades. Veamos eso en detalle.
Movimiento armónico simple
El movimiento armónico simple es un tipo de movimiento periódico en el que el objeto se mueve de un lado a otro alrededor de su posición media. El período de tiempo, en este caso, permanece constante. El período de tiempo se denota por «T» y la distancia de la posición media desde la posición extrema se llama amplitud, se denota por A. La ecuación general para la posición (x) del objeto en cualquier momento particular está dada por,
![]()
Aquí, ![]() y
y ![]() denota el cambio de fase.
denota el cambio de fase.
De manera similar, la ecuación para la velocidad del objeto en SHM se puede encontrar derivando esta ecuación.
![]()
Entonces, la ecuación para la aceleración se convierte en,
![]()
Energía en Movimiento Armónico Simple
Las energías cinética y potencial en el MAS varían desde cero hasta sus valores máximos. Las ecuaciones mencionadas anteriormente muestran que la velocidad del objeto sigue la trayectoria sinusoidal, lo que significa que la velocidad del objeto aumenta y disminuye. La velocidad es cero en las posiciones extremas y máxima en las posiciones medias. La posición donde la velocidad es máxima es la posición donde la energía cinética del objeto también es máxima.
Para un objeto de masa “m”, con una velocidad “v”. La energía cinética está dada por,
EC = ![]()
Dado que el objeto está en MAS, el valor de la velocidad se puede sustituir en la ecuación,
EC = ![]()
⇒ EC = ![]()
⇒ EC =![]()
Observe que la EC también tiene la forma de una ecuación periódica.
Valor máximo de KE = ![]() (En la posición media)
(En la posición media)
Valor mínimo de KE = 0 (En la posición extrema)
En el caso de fuerzas conservativas, que son directamente proporcionales al desplazamiento. La energía potencial está dada por,
tu = ![]()
Sustituyendo el valor de x(t) en MAS,
tu = ![]()
⇒ U(t) = ![]()
⇒ U(t) = ![]()
Encontremos la energía total,
mi = tu + k
⇒ mi = ![]() +
+ ![]()
⇒ mi = ![]()
⇒ mi = ![]()
La figura de arriba muestra el gráfico de KE y PE y la energía total E del SHM. En este caso, observe que la energía total del sistema permanece constante e independiente del tiempo.
Problemas de muestra
Pregunta 1: una partícula de 10 kg de masa está realizando MAS donde su posición está dada por la ecuación que se muestra a continuación,
x(t) = 3sen(5t)
Encuentre su energía cinética en la posición media.
Responder:
La EC en la posición media está dada por,
EC =
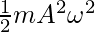
En este caso, A = 3, m = 10Kg y
EC =
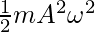
⇒ EC =
⇒ EC =
⇒ EC = 1225 J
Pregunta 2: Una partícula de 2 kg de masa está realizando MAS donde su posición está dada por la ecuación que se da a continuación,
x(t) = cos(2t)
Encuentre su energía cinética en la posición media.
Responder:
La EC en la posición media está dada por,
EC =
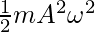
En este caso, A = 1, m = 2Kg y
EC =
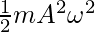
⇒ EC =
⇒ KE = 4 J.
Pregunta 3: Una partícula de 2Kg de masa está realizando MAS conectada a un resorte (k = 100 N/m) donde su posición está dada por la ecuación dada a continuación,
x(t) = 20 cos(t)
Encuentre su energía potencial en la posición extrema.
Responder:
La EC en la posición media está dada por,
U(t) =
En este caso, A = 20, k = 100 y
U(t) =
⇒ U(t) =
⇒ U(t) = 20000 J
Pregunta 4: Una partícula de 1Kg de masa está realizando MAS conectada a un resorte (k = 10 N/m) donde su posición está dada por la siguiente ecuación,
x(t) = 2 cos(t)
Encuentre su energía potencial en la posición extrema.
Responder:
La EC en la posición media está dada por,
U(t) =
En este caso, A = 2, k = 10 y
U(t) =
⇒ U(t) =
⇒ U(t) = 20J
Pregunta 5: una partícula está realizando MAS donde su posición está dada por la ecuación que se muestra a continuación,
x(t) = 2sen(10t)
Encuentre su velocidad en la posición media.
Responder:
La EC en la posición media está dada por,
EC =
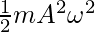
En este caso, A = 2 y
EC =
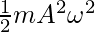
⇒
⇒
⇒
⇒ v = 10 m/s
Pregunta 6: Una partícula está realizando MAS donde su posición está dada por la ecuación que se da a continuación,
x(t) = 10cos(10t + 5)
Encuentre su velocidad en la posición media.
Responder:
La EC en la posición media está dada por,
EC =
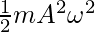
En este caso, A = 10 y
EC =
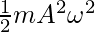
⇒
⇒
⇒v 2 = 10 2 (10) 2
⇒ v = 100 m/s
Publicación traducida automáticamente
Artículo escrito por anjalishukla1859 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA
