El potencial eléctrico en un lugar en un campo eléctrico es la cantidad de esfuerzo requerido para transportar una unidad de carga positiva desde el infinito hasta ese punto, mientras que la energía potencial eléctrica es la cantidad de energía requerida para mover una carga contra el campo eléctrico. La energía potencial gravitacional de una unidad de masa colocada en una determinada posición en el campo gravitatorio se denomina potencial gravitacional. En este sentido, la energía potencial eléctrica de una unidad de carga positiva en cualquier lugar del campo eléctrico es igual a la energía potencial eléctrica almacenada en una unidad de carga positiva en ese punto. El potencial eléctrico V en un punto dado del campo está dado por,
V = W/q
Si W es el trabajo realizado al transferir una unidad de carga positiva q desde el infinito hasta un punto particular del campo. Significa que el potencial eléctrico se mide en relación con algún punto de referencia y que solo podemos medir la diferencia de potencial entre dos puntos, similar a la energía potencial. La cantidad escalar es el potencial eléctrico. Un voltio es una unidad de medida que equivale al julio por culombio (J/C).
Diferencia de energía potencial
Considere el campo electrostático E que existe como resultado de un arreglo de carga. Considere el campo E causado por una carga Q colocada en el origen por simplicidad. Considere mover una carga de prueba q de un punto R a un punto P mientras resiste la fuerza repulsiva de la carga Q. Si Q y q son ambos positivos o ambos negativos, esto sucederá con la referencia. Usemos Q como ejemplo, con q > 0.

Una carga de prueba q (> 0) se mueve desde el punto R hasta el punto P contra la fuerza repulsiva sobre ella por la carga Q (> 0) colocada en el origen
Suponga que la carga de prueba q es tan pequeña que no tiene efecto sobre la configuración original, específicamente la carga Q en el origen (o que Q se mantiene fija en el origen por alguna fuerza desconocida). En segundo lugar, aplique una fuerza externa F ext exactamente lo suficiente como para contrarrestar la fuerza eléctrica repulsiva FE (es decir, F ext = –F E) a medida que la carga q se mueve de R a P. Esto significa que cuando la carga q se transporta de R a P, no experimenta fuerza neta ni aceleración, lo que implica que se transporta a una velocidad constante infinitesimalmente lenta. En este caso, el trabajo realizado por la fuerza externa es el inverso que es menos el trabajo realizado por la fuerza eléctrica, y la energía potencial de la carga q se almacena por completo. Si la fuerza externa se retira cuando la carga llega a P, la fuerza eléctrica alejará la carga de Q: la energía almacenada (energía potencial) en P se usa para proporcionar energía cinética a la carga q, preservando la suma de la energía cinética y energías potenciales.
Por lo tanto, el trabajo realizado por fuerzas externas al mover una carga q de R a P se puede escribir como,
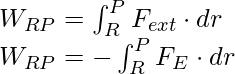
La expresión anterior es el trabajo realizado contra la fuerza opuesta electrostática y se almacena como energía potencial.
Una partícula con carga q tiene una energía potencial electrostática definida en cada lugar del campo eléctrico, y el trabajo realizado aumenta su energía potencial en una cantidad igual a la diferencia de energía potencial entre los puntos R y P. Por lo tanto, la diferencia de energía potencial puede ser expresado como,
∆U = U P – U R = W RP
Tenga en cuenta que este desplazamiento es en la dirección inversa de la fuerza eléctrica, por lo que el trabajo realizado por el campo eléctrico es negativo, es decir, -W RP .
Como resultado, el trabajo requerido por una fuerza externa para mover (sin acelerar) la carga q de un lugar a otro para un campo eléctrico de cualquier configuración de carga arbitraria puede definirse como la diferencia de energía potencial eléctrica entre dos puntos.
En este punto, se deben hacer dos puntos clave,
- El trabajo realizado por un campo electrostático al transferir una carga de un lugar a otro depende únicamente de los puntos inicial y final y no se ve afectado por el camino utilizado para llegar allí. Este es el atributo definitorio de una fuerza conservadora.
- La expresión anterior define la diferencia de energía potencial en términos de una cantidad de trabajo físicamente significativa. Dentro de una constante aditiva, la energía potencial es claramente incierta. Esto indica que el valor real de la energía potencial no tiene significado físico; sólo el cambio en la energía potencial es importante. Siempre podemos agregar una constante arbitraria a la energía potencial en cualquier momento ya que la diferencia de energía potencial no cambiará,
( UP – α ) – (U R – α ) = UP -U R
Dicho de otro modo, el punto donde la energía potencial es cero puede elegirse a voluntad. La energía potencial electrostática 0 en el infinito es una opción conveniente. Si tomamos el punto R en el infinito con esta opción,
W ∞P = UP PAGS – U ∞ = UP PAGS
La expresión anterior define la energía potencial de una carga q en cualquier momento.
El trabajo realizado por la fuerza externa (igual y opuesta a la fuerza eléctrica) al llevar la carga q desde el infinito hasta ese lugar (en presencia de un campo debido a cualquier configuración de carga) se denomina energía potencial de la carga q en un punto.
Potencial electrostático
En general, piense en cualquier configuración de carga estática. La energía potencial q de una carga de prueba se define en términos del trabajo realizado sobre ella. Este trabajo es obviamente proporcional a q porque la fuerza en cualquier posición es qE, donde E es el campo eléctrico en ese sitio debido a la disposición de carga dada. Como resultado, al dividir el trabajo por la carga q se obtiene una cantidad que es independiente de q. Para decirlo de otra manera, la cantidad de trabajo realizado por unidad de carga de prueba representa el campo eléctrico asociado con el arreglo de carga. Esto lleva al concepto de potencial electrostático V como resultado de un arreglo de carga particular.
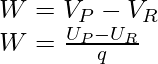
donde, V P y V R son los potenciales electrostáticos en P y R, respectivamente.
El trabajo realizado por una fuerza externa para transportar una unidad de carga positiva desde el infinito hasta un lugar es igual al potencial electrostático (V) en ese punto.
En otras palabras, el potencial electrostático (V ) en cualquier lugar de un área con un campo electrostático es el trabajo necesario para transportar una unidad de carga positiva desde el infinito hasta ese lugar (sin aceleración). La energía potencial eléctrica es una cantidad escalar sin dirección y solo magnitud. Está simbolizado por V y tiene la fórmula dimensional ML 2 T -3 A -1 .

El trabajo realizado sobre una carga de prueba q por el campo electrostático debido a cualquier configuración de carga dada es independiente del camino y depende solo de sus posiciones inicial y final.
Las mismas advertencias que se expresaron antes sobre la energía potencial se aplican a la definición de potencial. Para calcular el trabajo realizado por unidad de carga de prueba, comience con una carga de prueba infinitesimal δq, calcule el trabajo realizado δw al llevarlo desde el infinito hasta el punto y divídalo por δq para obtener la relación δW/δq. Además, en cada punto a lo largo del camino, la fuerza externa debe ser igual y opuesta a la fuerza electrostática que actúa sobre la carga de prueba.
Potencial eléctrico de una carga puntual

El trabajo realizado al llevar una unidad de carga de prueba positiva desde el infinito hasta el punto P, contra la fuerza repulsiva de la carga Q (Q > 0), es el potencial en P debido a la carga Q.
Observe el origen de una carga puntual Q. Considere que Q es un carácter positivo. Deseamos encontrar el potencial en cualquier ubicación P usando el vector de posición r desde el origen. Para hacerlo, necesitamos calcular cuánto trabajo se necesita para transferir una unidad de carga de prueba positiva desde el infinito hasta el punto P. Cuando Q > 0, el trabajo realizado contra la fuerza de repulsión en la carga de prueba es positivo. Como el trabajo es independiente de la trayectoria, elegimos una trayectoria conveniente, a lo largo de la dirección radial desde el infinito hasta el punto P.
La fuerza electrostática sobre una unidad de carga positiva en algún punto intermedio P′ en el camino es igual a
![]()
donde ![]() es el vector unitario a lo largo de OP′ por lo tanto, el trabajo realizado contra esta fuerza de r′ a r′ + ∆r′ se puede escribir como
es el vector unitario a lo largo de OP′ por lo tanto, el trabajo realizado contra esta fuerza de r′ a r′ + ∆r′ se puede escribir como
![]()
El signo negativo representa ∆r′ < 0, ∆W es positivo. El trabajo total realizado (W) por la fuerza externa se determina integrando la ecuación anterior en ambos lados, desde r′ = ∞ hasta r′ = r,
![Rendered by QuickLaTeX.com W=-\int_{∞}^{r} \frac{Q}{4\pi\epsilon_0r'^2}d{r'}\\ W=\left[\frac{Q}{4\pi\epsilon_0r'}\right]_∞^r\\ W=\frac{Q}{4\pi\epsilon_0r}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-d2e0180c3df582bd6cbe1919ff24155a_l3.png)
El potencial en P debido a la carga Q se puede expresar como
![]()
Energía potencial de un sistema de cargas

El potencial en un punto debido a un sistema de cargas es la suma de los potenciales debidos a las cargas individuales.
Supongamos un sistema de cargas q 1 , q 2 ,…, q n con vectores de posición r 1 , r 2 ,…, rn relativos a algún origen. El potencial V 1 en P debido a la carga q 1 se puede expresar como
![]()
donde r 1P es la distancia entre q 1 y P.
De manera similar, el potencial V 2 en P debido a q 2 y V 3 debido a q 3 se puede escribir como,
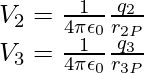
donde r 2P y r 3P son las distancias de P a las cargas q 2 y q 3 , respectivamente; y así sucesivamente para el potencial debido a otras cargas. Por el principio de superposición, el potencial V en P debido a la configuración de carga total es la suma algebraica de los potenciales debido a la carga individual, es decir,
V = V1 + V2 + V3 +…… + Vn
La expresión anterior se puede expresar como,
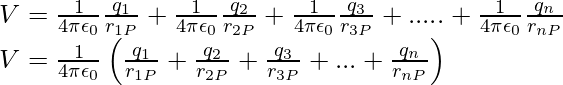
Es necesario dividir una distribución de carga continua con una densidad de carga (r) en pequeños elementos de volumen de tamaño ∆v, cada uno con una carga ρ∆v. Luego, para cada elemento de volumen, calcule el potencial y sume (o, más correctamente, integre) todas estas contribuciones para obtener el potencial general debido a la distribución.
Problemas de muestra
Problema 1: suponga que tiene una batería de motocicleta de 12,0 V que puede mover 5000 C de carga y una batería de automóvil de 12,0 V que puede mover 60 000 C de carga. ¿Cuánta energía entrega cada uno?
Solución:
Dado,
El valor de la batería es de 12,0 V, es decir, sus terminales tienen una diferencia de potencial de 12,0 V.
La carga que mueve la batería de la moto es de 5000 C.
La batería de automóvil de 12,0 V puede mover 60 000 C de carga.
Cuando una batería de este tipo mueve la carga, pasa la carga a través de una diferencia de potencial de 12,0 V, y la carga recibe un cambio en la energía potencial igual a ΔPE = qΔV.
Para la batería de la motocicleta, q = 5000 C y ΔV = 12,0 V. La energía total entregada por la batería de la motocicleta es
ΔPE motocicleta = (5000 C) × (12,0 V)
ΔPE motocicleta = 6,00 × 10 4 J
Ahora, para la batería del coche,
ΔPE coche = (60.000 C) × (12,0 V)
ΔPE coche =7.20 × 10 5 J
Problema 2: Una partícula de 40 mg de masa y con una carga de 5 × 10 -9 C se mueve directamente hacia una carga puntual positiva fija de magnitud 10 -8 C. Cuando está a una distancia de 10 cm de la carga puntual fija, tiene una velocidad de 50 cm/s. ¿A qué distancia de la carga puntual fija la partícula se detendrá momentáneamente? ¿La aceleración es constante durante el movimiento?
Solución:
Dado,
La masa de la partícula es de 40 mg.
La carga de la partícula es 5×10 -9 C.
La carga puntual positiva fija de magnitud 10 -8 C.
La partícula se detiene momentáneamente a una distancia r de la carga fija, por conservación de la energía tenemos,
Según la ley de conservación de la energía, la energía total del sistema = Constante
es decir (KE + PE) = constante.
La expresión de la energía cinética se puede expresar como,
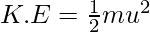
La expresión de la energía potencial se puede expresar como,
Ahora,
(1/2)mu 2 + (1/4)πε o × [Qq/a] = (1/4)πε o × [Qq/r]
Sustituyendo los valores en la ecuación anterior,
1/2 × 40 × 10 -6 × 1/2 × 1/2 = 9 × 10 9 × 10 -8 × 5 × 10 -9 × [ 1/r – 1/(10 × 10 -2 )]
o, [1/r – 10] = (5×10 -5 )/(9×5×10 -8 ) = 100/9
o bien, 1/r = (100/9) + 10
o bien, 1/r = 190/9 m
o r = 4,7 × 10 -2 m
Dado que, F = [1/4πεo] × [Qq/r2]
Por lo tanto, aceleración = F/m ∝ 1/r2, es decir, la aceleración no es constante durante el movimiento.
Problema 3: Una bola de masa 5 g y carga 10 -7 C se mueve desde el punto A cuyo potencial es 500 V hasta un punto B cuyo potencial es cero. ¿Cuál es la velocidad de la pelota en el punto A, si en el punto B es de 25 cm por segundo?
Solución:
Dado,
La bola de masa es de 5 g.
La carga de la partícula es de 10 -7 C.
El potencial de la bola en el punto A es de 500 V y el potencial en el punto B es cero.
Supongamos que u es la velocidad de la pelota en el punto A.
El trabajo realizado sobre la carga por el campo dado por,
W = q × (V A – V B )
Sustituya el valor en la expresión anterior,
W = 10 -7 × (500 – 0)
ancho = 5 × 10 -5 J
Por lo tanto,
W = (1/2) mv 2 – (1/2) mu 2
5 × 10 -5 = (1/2) × 5/1000 [(1/4) 2 – u 2 ]
2 × 10 -2 = 1/16 – tu 2
tu 2 = (1/16) – 0.02
u = (1- 0,32)/16
tu = 0.0425
Por lo tanto, u = 0,206 m/s
u = 20,6 cm/seg.
Problema 4: cuando una batería de automóvil de 12,0 V hace funcionar un solo faro de 30,0 W, ¿cuántos electrones pasan a través de él cada segundo?
Solución:
La expresión de la energía potencial se puede escribir como,
ΔPE = qΔV
Reorganizar la expresión anterior,
q = ΔPE/ΔV
Sustituya los valores en la ecuación anterior,
q = −30,0 J/ 12,0 V
q = −30,0 J/ 12,0 J/C
q = −2.50C
El número de electrones n se puede calcular como,
n = q/e
n = −2,50 C/(−1,60 × 10 −19 C/e)
n = 1,56 × 10 19 electrones
Problema 5: ¿Cuánto trabajo se requiere realizar para llevar dos cargas de magnitud 3C y 5C desde una separación de distancia infinita hasta una separación de 0,5 m?
Solución:
Dado,
Dos cargas de magnitud 3C y 5C.
La separación entre dos cargas es de 0,5 m.
El potencial en P debido a la carga Q se puede expresar como
∆E = mi 0 – mi gramo
∆E = 0 – [-(9 × 10 9 × 5 × 3)/0,5] = 27 × 10 10 .
Por lo tanto, ∆E = 27 × 10 10 V.
Publicación traducida automáticamente
Artículo escrito por anoopraj758 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA