Se dice que la entropía en la programación R es una medida del contaminante o la ambigüedad existente en los datos. Es un componente decisivo al dividir los datos a través de un árbol de decisión. Una muestra sin dividir tiene una entropía igual a cero, mientras que una muestra con partes igualmente divididas tiene una entropía igual a uno. Dos factores principales que se consideran al elegir un árbol apropiado son: ganancia de información (IG) y entropía.
Fórmula :
donde, p(x) es la probabilidad
Por ejemplo, considere un conjunto de datos escolares de un árbol de decisión cuya entropía debe calcularse.
| biblioteca disponible | El entrenador se unió | educación de los padres | rendimiento del estudiante |
|---|---|---|---|
| sí | sí | deseducado | malo |
| sí | no | deseducado | malo |
| no | no | educado | bueno |
| no | no | deseducado | malo |
Por lo tanto, se ve claramente que el desempeño de un estudiante se ve afectado por tres factores: la biblioteca disponible, el entrenamiento al que se unió y la educación de los padres. Se puede construir un árbol de decisión utilizando la información de estas tres variables para la predicción del rendimiento del estudiante y, por lo tanto, se denominan variables predictoras. Las variables con más información se consideran mejor separadoras del árbol de decisión.
Entonces, para calcular la entropía del Node principal: el rendimiento del estudiante, se usa la fórmula de entropía anterior, pero primero se debe calcular la probabilidad.
Hay cuatro valores en la columna de rendimiento del estudiante, de los cuales dos son buenos y dos son malos.

Por lo tanto, la entropía total del padre se puede calcular de la siguiente manera
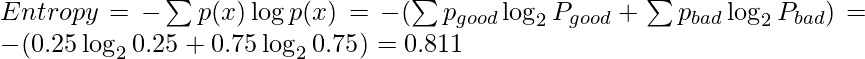
Ganancia de información usando entropía
La ganancia de información es un parámetro que se utiliza para decidir la mejor variable disponible para dividir los datos en cada Node del árbol de decisión. Por lo tanto, se puede calcular el IG de cada variable predictora y la variable con el IG más alto gana la carrera del factor decisivo para la división de los Nodes raíz.
Fórmula:
Ganancia de información (IG) = padre de entropía – (promedio ponderado * hijos de entropía )
Ahora, para calcular el IG de la variable predictora a la que se unió el coaching, primero divida el Node principal de acuerdo con esta variable.
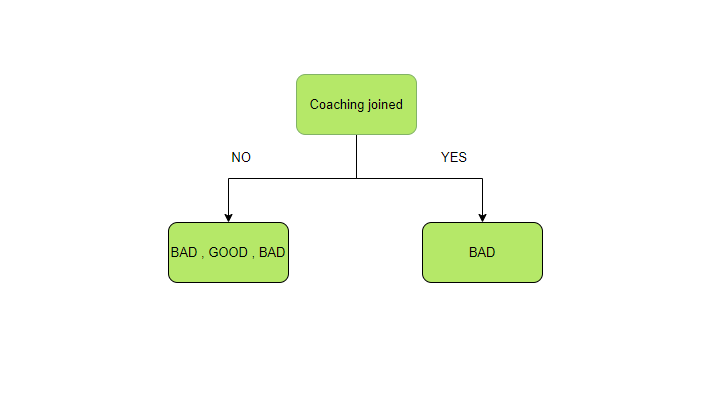
Ahora hay dos partes y su entropía primero se calcula individualmente.
La entropía de la parte izquierda.
Hay dos tipos de resultados disponibles: buenos y malos. En la parte izquierda, hay tres resultados totales, dos malos y uno bueno. Por lo tanto, P bueno y P malo se calcula nuevamente de la siguiente manera:

La entropía de la parte derecha
Sólo hay un componente en el derecho, es decir, el mal desempeño. Por lo tanto, la probabilidad se convierte en uno. Y la entropía se vuelve 0 porque solo hay una categoría a la que puede pertenecer la salida.
Cálculo del promedio ponderado con Entropía de niños

Hay 3 resultados en el Node secundario izquierdo y 1 en el Node derecho. Mientras que el Node izquierdo de Entropía se ha calculado como 0.9 y el Node derecho de Entropía es 0.
Ahora, manteniendo los valores en la fórmula anterior, obtenemos un promedio ponderado para este ejemplo:
![]()
Cálculo de IG
Ahora colocando el promedio ponderado calculado en la fórmula IG simplemente para obtener IG de ‘entrenamiento unido’.
IG(coaching joined) = Entropyparent - (weighted average * Entropychildren) IG(coaching joined) = 0.811 - 0.675 = 0.136
Usando los mismos pasos y fórmula, se calcula, compara y compara la IG de otras variables predictoras y, por lo tanto, se selecciona la variable con la IG más alta para dividir los datos en cada Node.