Escalares y Vectores – Barcelona Geeks

En física, las cantidades se pueden clasificar en escalares y vectores. Estas cantidades difieren solo por la dirección. Los vectores tienen asociada una dirección y una magnitud mientras que los escalares solo tienen una magnitud. Estas son cantidades que ocurren casi en cada parte del estudio del mundo físico. Por ejemplo, la distancia entre dos cantidades se puede medir y no necesita una dirección para expresarla, esto se llama cantidad escalar. Mientras que el movimiento de la partícula no se puede describir sin usar la dirección en la que se mueve. A esto se le llama cantidad vectorial. Estudiemos ambos tipos de cantidades en detalle.

Cantidades escalares y vectoriales

Las cantidades escalares son las cantidades que solo tienen un valor asociado a ellas. Estas cantidades se pueden expresar completamente con un solo número. Algunos ejemplos de cantidades escalares son: la masa de un objeto, la distancia entre dos puntos, etc. Para realizar operaciones en cantidades escalares, funcionan las reglas habituales del álgebra. Estas cantidades se pueden sumar y restar de la misma manera que se suman y restan los números.

Por otro lado, los vectores son cantidades que tienen asociada una dirección. Para la suma y la resta, estas cantidades obedecen la ley del triángulo de la suma de vectores. Algunos ejemplos de cantidades vectoriales incluyen velocidad, aceleración, etc. Al describir la velocidad, es necesario especificar la dirección. Los vectores están representados por $\vec{v}$ , que representa la dirección y la magnitud del vector. En el caso de la única magnitud, |v| denota la magnitud. La siguiente figura representa un vector. La longitud de la flecha representa la magnitud del vector.

Igualdad de Vectores

Se considera que dos vectores son iguales cuando tienen la misma magnitud y la misma dirección. La siguiente figura muestra dos vectores que son iguales, observe que estos vectores son paralelos entre sí y tienen la misma longitud. La segunda parte de la figura muestra dos vectores desiguales, que aunque tienen la misma magnitud, no son iguales porque tienen direcciones diferentes.

Multiplicación de Vectores con Escalar

Multiplicar un vector a con un escalar constante k da un vector cuya dirección es la misma pero la magnitud cambia por un factor de k. La figura muestra el vector antes y después de multiplicarlo por la constante k. En términos matemáticos, esto se puede reescribir como,

$|k\vec{v}| = k|\vec{v}|$

si k > 1, la magnitud del vector aumenta mientras que decrece cuando k < 1.

Adición de vectores

Los vectores no se pueden sumar por las reglas algebraicas habituales. Al sumar dos vectores, se debe tener en cuenta la magnitud y la dirección de los vectores. La ley del triángulo se usa para sumar dos vectores, el siguiente diagrama muestra dos vectores «a» y «b» y la resultante calculada después de su suma. La suma de vectores sigue la propiedad conmutativa, esto significa que el vector resultante es independiente del orden en que se suman los dos vectores.

$\vec{a} + \vec{b} = \vec{c}$

$\vec{a} + \vec{b} = \vec{b} + \vec{a}$ – (Propiedad conmutativa)

Ley del Triángulo de la Suma de Vectores

Considere los vectores dados en la figura anterior. La línea PQ representa el vector “p”, y QR representa el vector “q”. La línea QR representa el vector resultante. La dirección de AC es de A a C.

La línea AC representa,

$\vec{p} + \vec{q}$

La magnitud del vector resultante viene dada por,

$\sqrt{|p|^2 + |q|^2 + 2|p||q|cos(\theta)}$

El $\ theta$ representa el ángulo entre los dos vectores. Sea $\fi$ el ángulo que forma el vector resultante con el vector p.

$tan(\phi) = \frac{qsin(\theta)}{p + qcos(\theta)}$

Ley del paralelogramo de la suma de vectores

Esta ley es solo otra forma de entender la suma de vectores. Esta ley establece que si dos vectores que actúan sobre el mismo punto están representados por los lados del paralelogramo, entonces el vector resultante de estos vectores está representado por las diagonales de los paralelogramos. La siguiente figura muestra estos dos vectores representados en el lado del paralelogramo.

Problemas de muestra

Pregunta 1: Encuentra la magnitud de v = i + 4j.

Responder:

para un vector, v = ai + bj

|v| = $\sqrt{a^2 + b^2}$

a = 1, b = 4

|v| = $\sqrt{1^2 + 4^2}$

⇒ |v| = $\sqrt{1^2 + 4^2}$

⇒ |v| = √17

Pregunta 2: Un vector viene dado por, v = i + 4j. Encuentre la magnitud del vector cuando se escala por una constante de 5.

Responder:

para un vector, v = ai + bj

|v| = $\sqrt{a^2 + b^2}$

5|v| = |5v|

a = 1, b = 4

|5v|

⇒ |5(yo + 4j)|

⇒ |5i + 20j|

|v| = $\sqrt{5^2 + 20^2}$

⇒ |v| = $\sqrt{25 + 400}$

⇒ |v| = √425

Pregunta 3: Un vector viene dado por, v = i + j. Encuentre la magnitud del vector cuando se escala por una constante de 0.5.

Responder:

para un vector, v = ai + bj

|v| = $\sqrt{a^2 + b^2}$

0.5|v| = |0.5v|

a = 1, b = 1

|0.5v|

⇒ |0.5(yo + j)|

⇒ |0,5i + 0,5j|

|v| = $\sqrt{0.5^2 + 0.5^2}$

⇒ |v| = $\sqrt{0,25 + 0,25}$

⇒ |v| = √0.5

Pregunta 4: Dos vectores con magnitud 3 y 4. Estos vectores tienen un ángulo de 90° entre ellos. Encuentre la magnitud de los vectores resultantes.

Responder:

Sean los dos vectores dados por p y q. Entonces el vector resultante “r” está dado por,

$|r| = \sqrt{|p|^2 + |q|^2 + 2|p||q|cos(\theta)}$

|p| = 3, |q| = 4 y $\theta = 90^o$

$|r| = \sqrt{|p|^2 + |q|^2 + 2|p||q|cos(\theta)}$

⇒ $|r| = \sqrt{|3|^2 + |4|^2 + 2|3||4|cos(90)}$

⇒ $|r| = \sqrt{|3|^2 + |4|^2}$

⇒ $|r| = \sqrt{9 + 16}$

⇒ $|r| = \sqrt{9 + 16}$

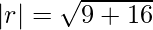
⇒ |r| = 5

Pregunta 5: Dos vectores con magnitud 10 y 9. Estos vectores tienen un ángulo de 60° entre ellos. Encuentre la magnitud de los vectores resultantes.

Responder:

Sean los dos vectores dados por p y q. Entonces el vector resultante “r” está dado por,

$|r| = \sqrt{|p|^2 + |q|^2 + 2|p||q|cos(\theta)}$

|p| = 10, |q| = 9 y $\theta = 60^o$

$|r| = \sqrt{|p|^2 + |q|^2 + 2|p||q|cos(\theta)}$

⇒ $|r| = \sqrt{|10|^2 + |9|^2 + 2|10||9|cos(60)}$

⇒ $|r| = \sqrt{|10|^2 + |9|^2 + (10)(9)}$

⇒ $|r| = \sqrt{100 + 81 + 90}$

⇒ $|r| = \sqrt{271}$

Pregunta 6: Dos vectores con magnitud 4 y 4. Estos vectores tienen un ángulo de 60° entre ellos. Encuentre la magnitud de los vectores resultantes y el ángulo formado por el vector resultante con 5.

Responder:

Sean los dos vectores dados por p y q. Entonces el vector resultante “r” está dado por,

$|r| = \sqrt{|p|^2 + |q|^2 + 2|p||q|cos(\theta)}$

|p| = 4, |q| = 4 y $\theta = 60^o$

$|r| = \sqrt{|p|^2 + |q|^2 + 2|p||q|cos(\theta)}$

⇒ $|r| = \sqrt{|4|^2 + |4|^2 + 2|4||4|cos(60)}$

⇒ $|r| = \sqrt{16 + 16 + 2|4||4|cos(60)}$

⇒ $|r| = \sqrt{48}$

⇒ |r| = 4√3

ángulo formado por la resultante,

$tan(\phi) = \frac{4sin(60)}{4 + 4cos(60)}$

⇒ $tan(\phi) = \frac{2\sqrt{2}}{4 + 2}$

⇒ $tan(\phi) = \frac{\sqrt{2}}{3}$

⇒ $\phi = tan{-1}(\frac{\sqrt{2}}{3})$