Hay dos listas enlazadas individualmente en un sistema. Por algún error de programación, el Node final de una de las listas vinculadas se vinculó a la segunda lista, formando una lista en forma de Y invertida. Escriba un programa para obtener el punto donde se fusionan dos listas enlazadas.
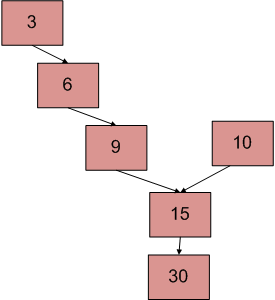
El diagrama anterior muestra un ejemplo con dos listas enlazadas que tienen 15 como puntos de intersección.
Método 1 (simplemente use dos bucles):
use 2 anidados para bucles. El bucle exterior será para cada Node de la primera lista y el bucle interior será para la segunda lista. En el bucle interno, verifique si alguno de los Nodes de la segunda lista es el mismo que el Node actual de la primera lista vinculada. La complejidad temporal de este método será O(M * N) donde m y n son los números de Nodes en dos listas.
A continuación se muestra el código para el enfoque anterior:
C++
// C++ program to get intersection point of two linked list
#include <bits/stdc++.h>
using namespace std;
/* Link list node */
class Node {
public:
int data;
Node* next;
};
/* function to get the intersection point of two linked
lists head1 and head2 */
Node* getIntesectionNode(Node* head1, Node* head2)
{
while (head2) {
Node* temp = head1;
while (temp) {
// if both Nodes are same
if (temp == head2)
return head2;
temp = temp->next;
}
head2 = head2->next;
}
// intersection is not present between the lists
return NULL;
}
// Driver Code
int main()
{
/*
Create two linked lists
1st 3->6->9->15->30
2nd 10->15->30
15 is the intersection point
*/
Node* newNode;
// Addition of new nodes
Node* head1 = new Node();
head1->data = 10;
Node* head2 = new Node();
head2->data = 3;
newNode = new Node();
newNode->data = 6;
head2->next = newNode;
newNode = new Node();
newNode->data = 9;
head2->next->next = newNode;
newNode = new Node();
newNode->data = 15;
head1->next = newNode;
head2->next->next->next = newNode;
newNode = new Node();
newNode->data = 30;
head1->next->next = newNode;
head1->next->next->next = NULL;
Node* intersectionPoint
= getIntesectionNode(head1, head2);
if (!intersectionPoint)
cout << " No Intersection Point \n";
else
cout << "Intersection Point: "
<< intersectionPoint->data << endl;
}
// This code is contributed by Tapesh(tapeshdua420)
C
// C program to get intersection point of two linked list
#include <stdio.h>
#include <stdlib.h>
/* Link list node */
typedef struct Node {
int data;
struct Node* next;
} Node;
/* function to get the intersection point of two linked
lists head1 and head2 */
Node* getIntesectionNode(Node* head1, Node* head2)
{
while (head2) {
Node* temp = head1;
while (temp) {
// if both Nodes are same
if (temp == head2)
return head2;
temp = temp->next;
}
head2 = head2->next;
}
// intersection is not present between the lists
return NULL;
}
// Driver Code
int main()
{
/*
Create two linked lists
1st 3->6->9->15->30
2nd 10->15->30
15 is the intersection point
*/
Node* newNode;
// Addition of new nodes
Node* head1 = (Node*)malloc(sizeof(Node));
head1->data = 10;
Node* head2 = (Node*)malloc(sizeof(Node));
head2->data = 3;
newNode = (Node*)malloc(sizeof(Node));
newNode->data = 6;
head2->next = newNode;
newNode = (Node*)malloc(sizeof(Node));
newNode->data = 9;
head2->next->next = newNode;
newNode = (Node*)malloc(sizeof(Node));
newNode->data = 15;
head1->next = newNode;
head2->next->next->next = newNode;
newNode = (Node*)malloc(sizeof(Node));
newNode->data = 30;
head1->next->next = newNode;
head1->next->next->next = NULL;
Node* intersectionPoint
= getIntesectionNode(head1, head2);
if (!intersectionPoint)
printf(" No Intersection Point \n");
else
printf("Intersection Point: %d\n",
intersectionPoint->data);
}
// This code is contributed by Aditya Kumar (adityakumar129)
Java
// Java Program to get intersection point of two linked
// lists.
class GFG {
static class Node {
int data;
Node next;
Node(int d)
{
data = d;
next = null;
}
}
/* function to get the intersection point of two linked
lists head1 and head2 */
public Node getIntersectionNode(Node head1, Node head2)
{
while (head2 != null) {
Node temp = head1;
while (temp != null) {
// if both Nodes are same
if (temp == head2) {
return head2;
}
temp = temp.next;
}
head2 = head2.next;
}
// If intersection is not present between the lists,
// return NULL.
return null;
}
public static void main(String[] args)
{
GFG list = new GFG();
Node head1, head2;
/*
Create two linked lists
1st 3->6->9->15->30
2nd 10->15->30
15 is the intersection point
*/
head1 = new Node(10);
head2 = new Node(3);
Node newNode = new Node(6);
head2.next = newNode;
newNode = new Node(9);
head2.next.next = newNode;
newNode = new Node(15);
head1.next = newNode;
head2.next.next.next = newNode;
newNode = new Node(30);
head1.next.next = newNode;
head1.next.next.next = null;
Node intersectionPoint
= list.getIntersectionNode(head1, head2);
if (intersectionPoint == null) {
System.out.print(" No Intersection Point \n");
}
else {
System.out.print("Intersection Point: "
+ intersectionPoint.data);
}
}
}
// This code is contributed by lokesh (lokeshmvs21).
Python3
# Python program to get intersection point of two linked list
# Link list node
class Node:
def __init__(self, data):
self.data = data
self.next = None
# function to get the intersection point of two linked lists head1 and head
def getIntersectionNode(head1, head2):
while head2:
temp = head1
while temp:
# if both Nodes are same
if temp == head2:
return head2
temp = temp.next
head2 = head2.next
# intersection is not present between the lists
return None
# Driver Code
if __name__ == '__main__':
'''
Create two linked lists
1st 3->6->9->15->30
2nd 10->15->30
15 is the intersection point
'''
newNode = Node(10)
head1 = newNode
newNode = Node(3)
head2 = newNode
newNode = Node(6)
head2.next = newNode
newNode = Node(9)
head2.next.next = newNode
newNode = Node(15)
head1.next = newNode
head2.next.next.next = newNode
newNode = Node(30)
head1.next.next = newNode
intersectionPoint = getIntersectionNode(head1, head2)
if not intersectionPoint:
print(" No Intersection Point ")
else:
print("Intersection Point:", intersectionPoint.data)
# This code is contributed by Tapesh(tapeshdua420)
C#
// C# program to get intersection point of two linked
// lists.
using System;
class GFG {
public class Node {
public int data;
public Node next;
public Node(int d)
{
data = d;
next = null;
}
}
/* function to get the intersection point of two linked
* lists head1 and head2 */
public Node getIntersectionNode(Node head1, Node head2)
{
while (head2 != null) {
Node temp = head1;
while (temp != null)
{
// if both Nodes are same
if (temp == head2) {
return head2;
}
temp = temp.next;
}
head2 = head2.next;
}
// If intersection is not present between the lists,
// return NULL.
return null;
}
public static void Main(string[] args)
{
GFG list = new GFG();
Node head1, head2;
/*
Create two linked lists
1st 3->6->9->15->30
2nd 10->15->30
15 is the intersection point
*/
head1 = new Node(10);
head2 = new Node(3);
Node newNode = new Node(6);
head2.next = newNode;
newNode = new Node(9);
head2.next.next = newNode;
newNode = new Node(15);
head1.next = newNode;
head2.next.next.next = newNode;
newNode = new Node(30);
head1.next.next = newNode;
head1.next.next.next = null;
Node intersectionPoint
= list.getIntersectionNode(head1, head2);
if (intersectionPoint == null) {
Console.Write(" No Intersection Point \n");
}
else {
Console.Write("Intersection Point: "
+ intersectionPoint.data);
}
}
}
// This code is contributed by Tapesh(tapeshdua420).
Intersection Point: 15
Método 2 (Marcar Nodes visitados):
esta solución requiere modificaciones en la estructura de datos básica de la lista vinculada. Tenga una bandera visitada con cada Node. Recorra la primera lista enlazada y siga marcando los Nodes visitados. Ahora recorra la segunda lista enlazada. Si vuelve a ver un Node visitado, entonces hay un punto de intersección, devuelva el Node de intersección. Esta solución funciona en O(m+n) pero requiere información adicional con cada Node. Se puede implementar una variación de esta solución que no requiere modificar la estructura de datos básica mediante un hash. Recorra la primera lista enlazada y almacene las direcciones de los Nodes visitados en un hash. Ahora recorra la segunda lista enlazada y si ve una dirección que ya existe en el hash, devuelva el Node de intersección.
Método 3 (usando la diferencia en el número de Nodes)
- Obtenga el conteo de los Nodes en la primera lista, deje que el conteo sea c1.
- Obtenga el conteo de los Nodes en la segunda lista, deje que el conteo sea c2.
- Obtener la diferencia de conteos d = abs(c1 – c2)
- Ahora recorra la lista más grande desde el primer Node hasta d Nodes para que de aquí en adelante ambas listas tengan el mismo número de Nodes.
- Entonces podemos recorrer ambas listas en paralelo hasta que encontremos un Node común. (Tenga en cuenta que obtener un Node común se realiza comparando la dirección de los Nodes)
La imagen de abajo es una ejecución en seco del enfoque anterior:

A continuación se muestra la implementación del enfoque anterior:
C++
// C++ program to get intersection point of two linked list
#include <bits/stdc++.h>
using namespace std;
/* Link list node */
class Node {
public:
int data;
Node* next;
};
/* Function to get the counts of node in a linked list */
int getCount(Node* head);
/* function to get the intersection point of two linked
lists head1 and head2 where head1 has d more nodes than
head2 */
int _getIntesectionNode(int d, Node* head1, Node* head2);
/* function to get the intersection point of two linked
lists head1 and head2 */
int getIntesectionNode(Node* head1, Node* head2)
{
// Count the number of nodes in
// both the linked list
int c1 = getCount(head1);
int c2 = getCount(head2);
int d;
// If first is greater
if (c1 > c2) {
d = c1 - c2;
return _getIntesectionNode(d, head1, head2);
}
else {
d = c2 - c1;
return _getIntesectionNode(d, head2, head1);
}
}
/* function to get the intersection point of two linked
lists head1 and head2 where head1 has d more nodes than
head2 */
int _getIntesectionNode(int d, Node* head1, Node* head2)
{
// Stand at the starting of the bigger list
Node* current1 = head1;
Node* current2 = head2;
// Move the pointer forward
for (int i = 0; i < d; i++) {
if (current1 == NULL) {
return -1;
}
current1 = current1->next;
}
// Move both pointers of both list till they
// intersect with each other
while (current1 != NULL && current2 != NULL) {
if (current1 == current2)
return current1->data;
// Move both the pointers forward
current1 = current1->next;
current2 = current2->next;
}
return -1;
}
/* Takes head pointer of the linked list and
returns the count of nodes in the list */
int getCount(Node* head)
{
Node* current = head;
// Counter to store count of nodes
int count = 0;
// Iterate till NULL
while (current != NULL) {
// Increase the counter
count++;
// Move the Node ahead
current = current->next;
}
return count;
}
// Driver Code
int main()
{
/*
Create two linked lists
1st 3->6->9->15->30
2nd 10->15->30
15 is the intersection point
*/
Node* newNode;
// Addition of new nodes
Node* head1 = new Node();
head1->data = 10;
Node* head2 = new Node();
head2->data = 3;
newNode = new Node();
newNode->data = 6;
head2->next = newNode;
newNode = new Node();
newNode->data = 9;
head2->next->next = newNode;
newNode = new Node();
newNode->data = 15;
head1->next = newNode;
head2->next->next->next = newNode;
newNode = new Node();
newNode->data = 30;
head1->next->next = newNode;
head1->next->next->next = NULL;
cout << "The node of intersection is " << getIntesectionNode(head1, head2);
}
// This code is contributed by rathbhupendra
C
// C program to get intersection point of two linked list
#include <stdio.h>
#include <stdlib.h>
/* Link list node */
struct Node {
int data;
struct Node* next;
};
/* Function to get the counts of node in a linked list */
int getCount(struct Node* head);
/* function to get the intersection point of two linked
lists head1 and head2 where head1 has d more nodes than
head2 */
int _getIntesectionNode(int d, struct Node* head1, struct Node* head2);
/* function to get the intersection point of two linked
lists head1 and head2 */
int getIntesectionNode(struct Node* head1, struct Node* head2)
{
int c1 = getCount(head1);
int c2 = getCount(head2);
int d;
if (c1 > c2) {
d = c1 - c2;
return _getIntesectionNode(d, head1, head2);
}
else {
d = c2 - c1;
return _getIntesectionNode(d, head2, head1);
}
}
/* function to get the intersection point of two linked
lists head1 and head2 where head1 has d more nodes than
head2 */
int _getIntesectionNode(int d, struct Node* head1, struct Node* head2)
{
int i;
struct Node* current1 = head1;
struct Node* current2 = head2;
for (i = 0; i < d; i++) {
if (current1 == NULL) {
return -1;
}
current1 = current1->next;
}
while (current1 != NULL && current2 != NULL) {
if (current1 == current2)
return current1->data;
current1 = current1->next;
current2 = current2->next;
}
return -1;
}
/* Takes head pointer of the linked list and
returns the count of nodes in the list */
int getCount(struct Node* head)
{
struct Node* current = head;
int count = 0;
while (current != NULL) {
count++;
current = current->next;
}
return count;
}
/* IGNORE THE BELOW LINES OF CODE. THESE LINES
ARE JUST TO QUICKLY TEST THE ABOVE FUNCTION */
int main()
{
/*
Create two linked lists
1st 3->6->9->15->30
2nd 10->15->30
15 is the intersection point
*/
struct Node* newNode;
struct Node* head1 = (struct Node*)malloc(sizeof(struct Node));
head1->data = 10;
struct Node* head2 = (struct Node*)malloc(sizeof(struct Node));
head2->data = 3;
newNode = (struct Node*)malloc(sizeof(struct Node));
newNode->data = 6;
head2->next = newNode;
newNode = (struct Node*)malloc(sizeof(struct Node));
newNode->data = 9;
head2->next->next = newNode;
newNode = (struct Node*)malloc(sizeof(struct Node));
newNode->data = 15;
head1->next = newNode;
head2->next->next->next = newNode;
newNode = (struct Node*)malloc(sizeof(struct Node));
newNode->data = 30;
head1->next->next = newNode;
head1->next->next->next = NULL;
printf("\n The node of intersection is %d \n",
getIntesectionNode(head1, head2));
getchar();
}
Java
// Java program to get intersection point of two linked list
class LinkedList {
static Node head1, head2;
static class Node {
int data;
Node next;
Node(int d)
{
data = d;
next = null;
}
}
/*function to get the intersection point of two linked
lists head1 and head2 */
int getNode()
{
int c1 = getCount(head1);
int c2 = getCount(head2);
int d;
if (c1 > c2) {
d = c1 - c2;
return _getIntesectionNode(d, head1, head2);
}
else {
d = c2 - c1;
return _getIntesectionNode(d, head2, head1);
}
}
/* function to get the intersection point of two linked
lists head1 and head2 where head1 has d more nodes than
head2 */
int _getIntesectionNode(int d, Node node1, Node node2)
{
int i;
Node current1 = node1;
Node current2 = node2;
for (i = 0; i < d; i++) {
if (current1 == null) {
return -1;
}
current1 = current1.next;
}
while (current1 != null && current2 != null) {
if (current1.data == current2.data) {
return current1.data;
}
current1 = current1.next;
current2 = current2.next;
}
return -1;
}
/*Takes head pointer of the linked list and
returns the count of nodes in the list */
int getCount(Node node)
{
Node current = node;
int count = 0;
while (current != null) {
count++;
current = current.next;
}
return count;
}
public static void main(String[] args)
{
LinkedList list = new LinkedList();
// creating first linked list
list.head1 = new Node(3);
list.head1.next = new Node(6);
list.head1.next.next = new Node(9);
list.head1.next.next.next = new Node(15);
list.head1.next.next.next.next = new Node(30);
// creating second linked list
list.head2 = new Node(10);
list.head2.next = new Node(15);
list.head2.next.next = new Node(30);
System.out.println("The node of intersection is " + list.getNode());
}
}
// This code has been contributed by Mayank Jaiswal
Python3
# defining a node for LinkedList
class Node:
def __init__(self,data):
self.data=data
self.next=None
def getIntersectionNode(head1,head2):
#finding the total number of elements in head1 LinkedList
c1=getCount(head1)
#finding the total number of elements in head2 LinkedList
c2=getCount(head2)
#Traverse the bigger node by 'd' so that from that node onwards, both LinkedList
#would be having same number of nodes and we can traverse them together.
if c1 > c2:
d=c1-c2
return _getIntersectionNode(d,head1,head2)
else:
d=c2-c1
return _getIntersectionNode(d,head2,head1)
def _getIntersectionNode(d,head1,head2):
current1=head1
current2=head2
for i in range(d):
if current1 is None:
return -1
current1=current1.next
while current1 is not None and current2 is not None:
# Instead of values, we need to check if there addresses are same
# because there can be a case where value is same but that value is
#not an intersecting point.
if current1 is current2:
return current1.data # or current2.data ( the value would be same)
current1=current1.next
current2=current2.next
# Incase, we are not able to find our intersecting point.
return -1
#Function to get the count of a LinkedList
def getCount(node):
cur=node
count=0
while cur is not None:
count+=1
cur=cur.next
return count
if __name__ == '__main__':
# Creating two LinkedList
# 1st one: 3->6->9->15->30
# 2nd one: 10->15->30
# We can see that 15 would be our intersection point
# Defining the common node
common=Node(15)
#Defining first LinkedList
head1=Node(3)
head1.next=Node(6)
head1.next.next=Node(9)
head1.next.next.next=common
head1.next.next.next.next=Node(30)
# Defining second LinkedList
head2=Node(10)
head2.next=common
head2.next.next=Node(30)
print("The node of intersection is ",getIntersectionNode(head1,head2))
# The code is contributed by Ansh Gupta.
C#
// C# program to get intersection point of two linked list
using System;
class LinkedList {
Node head1, head2;
public class Node {
public int data;
public Node next;
public Node(int d)
{
data = d;
next = null;
}
}
/*function to get the intersection point of two linked
lists head1 and head2 */
int getNode()
{
int c1 = getCount(head1);
int c2 = getCount(head2);
int d;
if (c1 > c2) {
d = c1 - c2;
return _getIntesectionNode(d, head1, head2);
}
else {
d = c2 - c1;
return _getIntesectionNode(d, head2, head1);
}
}
/* function to get the intersection point of two linked
lists head1 and head2 where head1 has d more nodes than
head2 */
int _getIntesectionNode(int d, Node node1, Node node2)
{
int i;
Node current1 = node1;
Node current2 = node2;
for (i = 0; i < d; i++) {
if (current1 == null) {
return -1;
}
current1 = current1.next;
}
while (current1 != null && current2 != null) {
if (current1.data == current2.data) {
return current1.data;
}
current1 = current1.next;
current2 = current2.next;
}
return -1;
}
/*Takes head pointer of the linked list and
returns the count of nodes in the list */
int getCount(Node node)
{
Node current = node;
int count = 0;
while (current != null) {
count++;
current = current.next;
}
return count;
}
public static void Main(String[] args)
{
LinkedList list = new LinkedList();
// creating first linked list
list.head1 = new Node(3);
list.head1.next = new Node(6);
list.head1.next.next = new Node(9);
list.head1.next.next.next = new Node(15);
list.head1.next.next.next.next = new Node(30);
// creating second linked list
list.head2 = new Node(10);
list.head2.next = new Node(15);
list.head2.next.next = new Node(30);
Console.WriteLine("The node of intersection is " + list.getNode());
}
}
// This code is contributed by Arnab Kundu
Javascript
<script>
class Node
{
constructor(item)
{
this.data=item;
this.next=null;
}
}
let head1,head2;
function getNode()
{
let c1 = getCount(head1);
let c2 = getCount(head2);
let d;
if (c1 > c2) {
d = c1 - c2;
return _getIntesectionNode(d, head1, head2);
}
else {
d = c2 - c1;
return _getIntesectionNode(d, head2, head1);
}
}
function _getIntesectionNode(d,node1,node2)
{
let i;
let current1 = node1;
let current2 = node2;
for (i = 0; i < d; i++) {
if (current1 == null) {
return -1;
}
current1 = current1.next;
}
while (current1 != null && current2 != null) {
if (current1.data == current2.data) {
return current1.data;
}
current1 = current1.next;
current2 = current2.next;
}
return -1;
}
function getCount(node)
{
let current = node;
let count = 0;
while (current != null) {
count++;
current = current.next;
}
return count;
}
head1 = new Node(3);
head1.next = new Node(6);
head1.next.next = new Node(9);
head1.next.next.next = new Node(15);
head1.next.next.next.next = new Node(30);
// creating second linked list
head2 = new Node(10);
head2.next = new Node(15);
head2.next.next = new Node(30);
document.write("The node of intersection is " + getNode());
// This code is contributed by avanitrachhadiya2155
</script>
The node of intersection is 15
Complejidad temporal: O(m+n)
Espacio auxiliar: O(1)
Método 4 (haga un círculo en la primera lista)
Gracias a Saravanan Man por proporcionar la solución a continuación.
1. Recorra la primera lista enlazada (cuente los elementos) y haga una lista enlazada circular. (Recuerde el último Node para que podamos romper el círculo más adelante).
2. Ahora vea el problema como encontrar el bucle en la segunda lista enlazada. Así que el problema está resuelto.
3. Como ya conocemos la longitud del bucle (tamaño de la primera lista enlazada), podemos recorrer esa cantidad de Nodes en la segunda lista y luego iniciar otro puntero desde el comienzo de la segunda lista. tenemos que atravesar hasta que sean iguales, y ese es el punto de intersección requerido.
4. elimine el círculo de la lista vinculada.
Complejidad temporal: O(m+n)
Espacio auxiliar: O(1)
Método 5 (Invertir la primera lista y hacer ecuaciones)
Gracias a Saravanan Mani por proporcionar este método.
1) Let X be the length of the first linked list until intersection point.
Let Y be the length of the second linked list until the intersection point.
Let Z be the length of the linked list from the intersection point to End of
the linked list including the intersection node.
We Have
X + Z = C1;
Y + Z = C2;
2) Reverse first linked list.
3) Traverse Second linked list. Let C3 be the length of second list - 1.
Now we have
X + Y = C3
We have 3 linear equations. By solving them, we get
X = (C1 + C3 – C2)/2;
Y = (C2 + C3 – C1)/2;
Z = (C1 + C2 – C3)/2;
WE GOT THE INTERSECTION POINT.
4) Reverse first linked list.
Ventaja: No hay comparación de punteros.
Desventaja: modificación de la lista enlazada (lista de inversión).
Complejidad temporal: O(m+n)
Espacio auxiliar: O(1)
Método 6 (Recorre ambas listas y compara las direcciones de los últimos Nodes) Este método es solo para detectar si hay un punto de intersección o no. (Gracias a NeoTheSaviour por sugerir esto)
1) Traverse the list 1, store the last node address 2) Traverse the list 2, store the last node address. 3) If nodes stored in 1 and 2 are same then they are intersecting.
La complejidad temporal de este método es O(m+n) y el espacio auxiliar utilizado es O(1)
Método 7 (Usar Hashing)
Básicamente, necesitamos encontrar un Node común de dos listas enlazadas. Así que hacemos hash de todos los Nodes de la primera lista y luego verificamos la segunda lista.
1) Cree un conjunto hash vacío.
2) Atraviese la primera lista enlazada e inserte las direcciones de todos los Nodes en el conjunto hash.
3) Recorrer la segunda lista. Para cada Node, compruebe si está presente en el conjunto hash. Si encontramos un Node en el conjunto hash, devolvemos el Node.
C++
// C++ program to get intersection point of two linked list
#include <iostream>
#include <unordered_set>
using namespace std;
class Node
{
public:
int data;
Node* next;
Node(int d)
{
data = d;
next = NULL;
}
};
// function to find the intersection point of two lists
void MegeNode(Node* n1, Node* n2)
{
unordered_set<Node*> hs;
while (n1 != NULL) {
hs.insert(n1);
n1 = n1->next;
}
while (n2) {
if (hs.find(n2) != hs.end()) {
cout << n2->data << endl;
break;
}
n2 = n2->next;
}
}
// function to print the list
void Print(Node* n)
{
Node* curr = n;
while(curr != NULL){
cout << curr->data << " ";
curr = curr->next;
}
cout << endl;
}
int main()
{
// list 1
Node* n1 = new Node(1);
n1->next = new Node(2);
n1->next->next = new Node(3);
n1->next->next->next = new Node(4);
n1->next->next->next->next = new Node(5);
n1->next->next->next->next->next = new Node(6);
n1->next->next->next->next->next->next = new Node(7);
// list 2
Node* n2 = new Node(10);
n2->next = new Node(9);
n2->next->next = new Node(8);
n2->next->next->next = n1->next->next->next;
Print(n1);
Print(n2);
MegeNode(n1,n2);
return 0;
}
// This code is contributed by Upendra
Java
// Java program to get intersection point of two linked list
import java.util.*;
class Node {
int data;
Node next;
Node(int d)
{
data = d;
next = null;
}
}
class LinkedListIntersect {
public static void main(String[] args)
{
// list 1
Node n1 = new Node(1);
n1.next = new Node(2);
n1.next.next = new Node(3);
n1.next.next.next = new Node(4);
n1.next.next.next.next = new Node(5);
n1.next.next.next.next.next = new Node(6);
n1.next.next.next.next.next.next = new Node(7);
// list 2
Node n2 = new Node(10);
n2.next = new Node(9);
n2.next.next = new Node(8);
n2.next.next.next = n1.next.next.next;
Print(n1);
Print(n2);
System.out.println(MegeNode(n1, n2).data);
}
// function to print the list
public static void Print(Node n)
{
Node cur = n;
while (cur != null) {
System.out.print(cur.data + " ");
cur = cur.next;
}
System.out.println();
}
// function to find the intersection of two node
public static Node MegeNode(Node n1, Node n2)
{
// define hashset
HashSet<Node> hs = new HashSet<Node>();
while (n1 != null) {
hs.add(n1);
n1 = n1.next;
}
while (n2 != null) {
if (hs.contains(n2)) {
return n2;
}
n2 = n2.next;
}
return null;
}
}
Python3
# Python program to get intersection
# point of two linked list
class Node :
def __init__(self, d):
self.data = d;
self.next = None;
# Function to print the list
def Print(n):
cur = n;
while (cur != None) :
print(cur.data, end=" ");
cur = cur.next;
print("");
# Function to find the intersection of two node
def MegeNode(n1, n2):
# Define hashset
hs = set();
while (n1 != None):
hs.add(n1);
n1 = n1.next;
while (n2 != None):
if (n2 in hs):
return n2;
n2 = n2.next;
return None;
# Driver code
# list 1
n1 = Node(1);
n1.next = Node(2);
n1.next.next = Node(3);
n1.next.next.next = Node(4);
n1.next.next.next.next = Node(5);
n1.next.next.next.next.next = Node(6);
n1.next.next.next.next.next.next = Node(7);
# list 2
n2 = Node(10);
n2.next = Node(9);
n2.next.next = Node(8);
n2.next.next.next = n1.next.next.next;
Print(n1);
Print(n2);
print(MegeNode(n1, n2).data);
# This code is contributed by _saurabh_jaiswal
C#
// C# program to get intersection point of two linked list
using System;
using System.Collections.Generic;
public class Node
{
public int data;
public Node next;
public Node(int d)
{
data = d;
next = null;
}
}
public class LinkedListIntersect
{
public static void Main(String[] args)
{
// list 1
Node n1 = new Node(1);
n1.next = new Node(2);
n1.next.next = new Node(3);
n1.next.next.next = new Node(4);
n1.next.next.next.next = new Node(5);
n1.next.next.next.next.next = new Node(6);
n1.next.next.next.next.next.next = new Node(7);
// list 2
Node n2 = new Node(10);
n2.next = new Node(9);
n2.next.next = new Node(8);
n2.next.next.next = n1.next.next.next;
Print(n1);
Print(n2);
Console.WriteLine(MegeNode(n1, n2).data);
}
// function to print the list
public static void Print(Node n)
{
Node cur = n;
while (cur != null)
{
Console.Write(cur.data + " ");
cur = cur.next;
}
Console.WriteLine();
}
// function to find the intersection of two node
public static Node MegeNode(Node n1, Node n2)
{
// define hashset
HashSet<Node> hs = new HashSet<Node>();
while (n1 != null)
{
hs.Add(n1);
n1 = n1.next;
}
while (n2 != null)
{
if (hs.Contains(n2))
{
return n2;
}
n2 = n2.next;
}
return null;
}
}
// This code is contributed by 29AjayKumar
Javascript
<script>
// Javascript program to get intersection
// point of two linked list
class Node
{
constructor(d)
{
this.data = d;
this.next = null;
}
}
// Function to print the list
function Print(n)
{
let cur = n;
while (cur != null)
{
document.write(cur.data + " ");
cur = cur.next;
}
document.write("<br>");
}
// Function to find the intersection of two node
function MegeNode(n1, n2)
{
// Define hashset
let hs = new Set();
while (n1 != null)
{
hs.add(n1);
n1 = n1.next;
}
while (n2 != null)
{
if (hs.has(n2))
{
return n2;
}
n2 = n2.next;
}
return null;
}
// Driver code
// list 1
let n1 = new Node(1);
n1.next = new Node(2);
n1.next.next = new Node(3);
n1.next.next.next = new Node(4);
n1.next.next.next.next = new Node(5);
n1.next.next.next.next.next = new Node(6);
n1.next.next.next.next.next.next = new Node(7);
// list 2
let n2 = new Node(10);
n2.next = new Node(9);
n2.next.next = new Node(8);
n2.next.next.next = n1.next.next.next;
Print(n1);
Print(n2);
document.write(MegeNode(n1, n2).data);
// This code is contributed by rag2127
</script>
1 2 3 4 5 6 7 10 9 8 4 5 6 7 4
Este método requiere O(n) espacio adicional y no es muy eficiente si una lista es grande.
Método 8 (técnica de 2 puntos):
Usando dos punteros:
- Inicialice dos punteros ptr1 y ptr2 en head1 y head2.
- Recorra las listas, un Node a la vez.
- Cuando ptr1 llegue al final de una lista, rediríjalo a head2.
- De manera similar, cuando ptr2 llegue al final de una lista, rediríjalo a head1.
- Una vez que ambos pasen por la reasignación, estarán equidistantes del
punto de colisión . - Si en algún Node ptr1 se encuentra con ptr2, entonces es el Node de intersección.
- Después de la segunda iteración, si no hay un Node de intersección, devuelve NULL.
C++
// CPP program to print intersection of lists
#include <bits/stdc++.h>
using namespace std;
/* Link list node */
class Node {
public:
int data;
Node* next;
};
// A utility function to return intersection node
Node* intersectPoint(Node* head1, Node* head2)
{
// Maintaining two pointers ptr1 and ptr2
// at the head of A and B,
Node* ptr1 = head1;
Node* ptr2 = head2;
// If any one of head is NULL i.e
// no Intersection Point
if (ptr1 == NULL || ptr2 == NULL)
return NULL;
// Traverse through the lists until they
// reach Intersection node
while (ptr1 != ptr2) {
ptr1 = ptr1->next;
ptr2 = ptr2->next;
// If at any node ptr1 meets ptr2, then it is
// intersection node.Return intersection node.
if (ptr1 == ptr2)
return ptr1;
/* Once both of them go through reassigning,
they will be equidistant from the collision point.*/
// When ptr1 reaches the end of a list, then
// reassign it to the head2.
if (ptr1 == NULL)
ptr1 = head2;
// When ptr2 reaches the end of a list, then
// redirect it to the head1.
if (ptr2 == NULL)
ptr2 = head1;
}
return ptr1;
}
// Function to print intersection nodes
// in a given linked list
void print(Node* node)
{
if (node == NULL)
cout << "NULL";
while (node->next != NULL) {
cout << node->data << "->";
node = node->next;
}
cout << node->data;
}
// Driver code
int main()
{
/*
Create two linked lists
1st Linked list is 3->6->9->15->30
2nd Linked list is 10->15->30
15 30 are elements in the intersection list
*/
Node* newNode;
Node* head1 = new Node();
head1->data = 10;
Node* head2 = new Node();
head2->data = 3;
newNode = new Node();
newNode->data = 6;
head2->next = newNode;
newNode = new Node();
newNode->data = 9;
head2->next->next = newNode;
newNode = new Node();
newNode->data = 15;
head1->next = newNode;
head2->next->next->next = newNode;
newNode = new Node();
newNode->data = 30;
head1->next->next = newNode;
head1->next->next->next = NULL;
Node* intersect_node = NULL;
// Find the intersection node of two linked lists
intersect_node = intersectPoint(head1, head2);
cout << "INTERSEPOINT LIST :";
print(intersect_node);
return 0;
}
// This code is contributed by Aditya Kumar (adityakumar129)
C
// c program to print intersection of lists
#include <stdio.h>
#include <stdlib.h>
/* Link list node */
typedef struct Node {
int data;
struct Node* next;
}Node;
// A utility function to return intersection node
Node* intersectPoint(Node* head1, Node* head2)
{
// Maintaining two pointers ptr1 and ptr2
// at the head of A and B,
Node* ptr1 = head1;
Node* ptr2 = head2;
// If any one of head is NULL i.e
// no Intersection Point
if (ptr1 == NULL || ptr2 == NULL)
return NULL;
// Traverse through the lists until they
// reach Intersection node
while (ptr1 != ptr2) {
ptr1 = ptr1->next;
ptr2 = ptr2->next;
// If at any node ptr1 meets ptr2, then it is
// intersection node.Return intersection node.
if (ptr1 == ptr2)
return ptr1;
/* Once both of them go through reassigning,
they will be equidistant from the collision point.*/
// When ptr1 reaches the end of a list, then
// reassign it to the head2.
if (ptr1 == NULL)
ptr1 = head2;
// When ptr2 reaches the end of a list, then
// redirect it to the head1.
if (ptr2 == NULL)
ptr2 = head1;
}
return ptr1;
}
// Function to print intersection nodes
// in a given linked list
void print(Node* node)
{
if (node == NULL)
printf("NULL");
while (node->next != NULL) {
printf("%d->", node->data);
node = node->next;
}
printf("%d", node->data);
}
// Driver code
int main()
{
/*
Create two linked lists
1st Linked list is 3->6->9->15->30
2nd Linked list is 10->15->30
15 30 are elements in the intersection list
*/
Node* newNode;
Node* head1 = (Node*)malloc(sizeof(Node));
head1->data = 10;
Node* head2 = (Node*)malloc(sizeof(Node));
head2->data = 3;
newNode = (Node*)malloc(sizeof(Node));
newNode->data = 6;
head2->next = newNode;
newNode = (Node*)malloc(sizeof(Node));
newNode->data = 9;
head2->next->next = newNode;
newNode = (Node*)malloc(sizeof(Node));
newNode->data = 15;
head1->next = newNode;
head2->next->next->next = newNode;
newNode = (Node*)malloc(sizeof(Node));
newNode->data = 30;
head1->next->next = newNode;
head1->next->next->next = NULL;
Node* intersect_node = NULL;
// Find the intersection node of two linked lists
intersect_node = intersectPoint(head1, head2);
printf("INTERSEPOINT LIST :");
print(intersect_node);
return 0;
}
// This code is contributed by Aditya Kumar (adityakumar129)
Java
// JAVA program to print intersection of lists
import java.util.*;
class GFG{
/* Link list node */
static class Node {
int data;
Node next;
};
// A utility function to return intersection node
static Node intersectPoint(Node head1, Node head2)
{
// Maintaining two pointers ptr1 and ptr2
// at the head of A and B,
Node ptr1 = head1;
Node ptr2 = head2;
// If any one of head is null i.e
// no Intersection Point
if (ptr1 == null || ptr2 == null) {
return null;
}
// Traverse through the lists until they
// reach Intersection node
while (ptr1 != ptr2) {
ptr1 = ptr1.next;
ptr2 = ptr2.next;
// If at any node ptr1 meets ptr2, then it is
// intersection node.Return intersection node.
if (ptr1 == ptr2) {
return ptr1;
}
/* Once both of them go through reassigning,
they will be equidistant from the collision point.*/
// When ptr1 reaches the end of a list, then
// reassign it to the head2.
if (ptr1 == null) {
ptr1 = head2;
}
// When ptr2 reaches the end of a list, then
// redirect it to the head1.
if (ptr2 == null) {
ptr2 = head1;
}
}
return ptr1;
}
// Function to print intersection nodes
// in a given linked list
static void print(Node node)
{
if (node == null)
System.out.print("null");
while (node.next != null) {
System.out.print(node.data+ ".");
node = node.next;
}
System.out.print(node.data);
}
// Driver code
public static void main(String[] args)
{
/*
Create two linked lists
1st Linked list is 3.6.9.15.30
2nd Linked list is 10.15.30
15 30 are elements in the intersection list
*/
Node newNode;
Node head1 = new Node();
head1.data = 10;
Node head2 = new Node();
head2.data = 3;
newNode = new Node();
newNode.data = 6;
head2.next = newNode;
newNode = new Node();
newNode.data = 9;
head2.next.next = newNode;
newNode = new Node();
newNode.data = 15;
head1.next = newNode;
head2.next.next.next = newNode;
newNode = new Node();
newNode.data = 30;
head1.next.next = newNode;
head1.next.next.next = null;
Node intersect_node = null;
// Find the intersection node of two linked lists
intersect_node = intersectPoint(head1, head2);
System.out.print("INTERSEPOINT LIST :");
print(intersect_node);
}
}
// This code is contributed by umadevi9616.
Python3
# Python3 program to print intersection of lists
# Link list node
class Node:
def __init__(self, data = 0, next = None):
self.data = data
self.next = next
# A utility function to return intersection node
def intersectPoint(head1, head2):
# Maintaining two pointers ptr1 and ptr2
# at the head of A and B,
ptr1 = head1
ptr2 = head2
# If any one of head is None i.e
# no Intersection Point
if (ptr1 == None or ptr2 == None):
return None
# Traverse through the lists until they
# reach Intersection node
while (ptr1 != ptr2):
ptr1 = ptr1.next
ptr2 = ptr2.next
# If at any node ptr1 meets ptr2, then it is
# intersection node.Return intersection node.
if (ptr1 == ptr2):
return ptr1
# Once both of them go through reassigning,
# they will be equidistant from the collision point.
# When ptr1 reaches the end of a list, then
# reassign it to the head2.
if (ptr1 == None):
ptr1 = head2
# When ptr2 reaches the end of a list, then
# redirect it to the head1.
if (ptr2 == None):
ptr2 = head1
return ptr1
# Function to print intersection nodes
# in a given linked list
def Print(node):
if (node == None):
print("None")
while (node.next != None):
print(node.data,end="->")
node = node.next
print(node.data)
# Driver code
# Create two linked lists
# 1st Linked list is 3->6->9->15->30
# 2nd Linked list is 10->15->30
# 15 30 are elements in the intersection list
head1 = Node()
head1.data = 10
head2 = Node()
head2.data = 3
newNode = Node()
newNode.data = 6
head2.next = newNode
newNode = Node()
newNode.data = 9
head2.next.next = newNode
newNode = Node()
newNode.data = 15
head1.next = newNode
head2.next.next.next = newNode
newNode = Node()
newNode.data = 30
head1.next.next = newNode
head1.next.next.next = None
intersect_node = None
# Find the intersection node of two linked lists
intersect_node = intersectPoint(head1, head2)
print("INTERSEPOINT LIST :",end="")
Print(intersect_node)
# This code is contributed by shinjanpatra
C#
// C# program to print intersection of lists
using System;
public class GFG {
/* Link list node */
public
class Node {
public
int data;
public
Node next;
};
// A utility function to return intersection node
static Node intersectPoint(Node head1, Node head2) {
// Maintaining two pointers ptr1 and ptr2
// at the head of A and B,
Node ptr1 = head1;
Node ptr2 = head2;
// If any one of head is null i.e
// no Intersection Point
if (ptr1 == null || ptr2 == null) {
return null;
}
// Traverse through the lists until they
// reach Intersection node
while (ptr1 != ptr2) {
ptr1 = ptr1.next;
ptr2 = ptr2.next;
// If at any node ptr1 meets ptr2, then it is
// intersection node.Return intersection node.
if (ptr1 == ptr2) {
return ptr1;
}
/*
* Once both of them go through reassigning, they will be equidistant from the
* collision point.
*/
// When ptr1 reaches the end of a list, then
// reassign it to the head2.
if (ptr1 == null) {
ptr1 = head2;
}
// When ptr2 reaches the end of a list, then
// redirect it to the head1.
if (ptr2 == null) {
ptr2 = head1;
}
}
return ptr1;
}
// Function to print intersection nodes
// in a given linked list
static void print(Node node) {
if (node == null)
Console.Write("null");
while (node.next != null) {
Console.Write(node.data + "->");
node = node.next;
}
Console.Write(node.data);
}
// Driver code
public static void Main(String[] args)
{
/*
* Create two linked lists
*
* 1st Linked list is 3.6.9.15.30 2nd Linked list is 10.15.30
*
* 15 30 are elements in the intersection list
*/
Node newNode;
Node head1 = new Node();
head1.data = 10;
Node head2 = new Node();
head2.data = 3;
newNode = new Node();
newNode.data = 6;
head2.next = newNode;
newNode = new Node();
newNode.data = 9;
head2.next.next = newNode;
newNode = new Node();
newNode.data = 15;
head1.next = newNode;
head2.next.next.next = newNode;
newNode = new Node();
newNode.data = 30;
head1.next.next = newNode;
head1.next.next.next = null;
Node intersect_node = null;
// Find the intersection node of two linked lists
intersect_node = intersectPoint(head1, head2);
Console.Write("INTERSEPOINT LIST :");
print(intersect_node);
}
}
// This code is contributed by gauravrajput1
Javascript
<script>
// Javascript program to print intersection of lists
/* Link list node */
class Node {
constructor() {
this.data = null;
this.next = null;
}
};
// A utility function to return intersection node
function intersectPoint(head1, head2) {
// Maintaining two pointers ptr1 and ptr2
// at the head of A and B,
let ptr1 = head1;
let ptr2 = head2;
// If any one of head is null i.e
// no Intersection Point
if (ptr1 == null || ptr2 == null) {
return null;
}
// Traverse through the lists until they
// reach Intersection node
while (ptr1 != ptr2) {
ptr1 = ptr1.next;
ptr2 = ptr2.next;
// If at any node ptr1 meets ptr2, then it is
// intersection node.Return intersection node.
if (ptr1 == ptr2) {
return ptr1;
}
/* Once both of them go through reassigning,
they will be equidistant from the collision point.*/
// When ptr1 reaches the end of a list, then
// reassign it to the head2.
if (ptr1 == null) {
ptr1 = head2;
}
// When ptr2 reaches the end of a list, then
// redirect it to the head1.
if (ptr2 == null) {
ptr2 = head1;
}
}
return ptr1;
}
// Function to print intersection nodes
// in a given linked list
function print(node) {
if (node == null)
document.write("null");
while (node.next != null) {
document.write(node.data + "->");
node = node.next;
}
document.write(node.data);
}
// Driver code
/*
Create two linked lists
1st Linked list is 3.6.9.15.30
2nd Linked list is 10.15.30
15 30 are elements in the intersection list
*/
let newNode;
let head1 = new Node();
head1.data = 10;
let head2 = new Node();
head2.data = 3;
newNode = new Node();
newNode.data = 6;
head2.next = newNode;
newNode = new Node();
newNode.data = 9;
head2.next.next = newNode;
newNode = new Node();
newNode.data = 15;
head1.next = newNode;
head2.next.next.next = newNode;
newNode = new Node();
newNode.data = 30;
head1.next.next = newNode;
head1.next.next.next = null;
let intersect_node = null;
// Find the intersection node of two linked lists
intersect_node = intersectPoint(head1, head2);
document.write("INTERSEPOINT LIST :");
print(intersect_node);
// This code is contributed by Saurabh Jaiswal
</script>
INTERSEPOINT LIST :15->30
Complejidad temporal: O( m + n )
Espacio auxiliar: O(1)
Escriba comentarios si encuentra algún error en el algoritmo anterior o una mejor manera de resolver el mismo problema.
Publicación traducida automáticamente
Artículo escrito por GeeksforGeeks-1 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA
