Estabilidad en los algoritmos de clasificación.

La estabilidad es principalmente importante cuando tenemos pares de valores clave con posibles claves duplicadas (como nombres de personas como claves y sus detalles como valores). Y deseamos ordenar estos objetos por claves.

¿Qué es?
Se dice que un algoritmo de ordenación es estable si dos objetos con claves iguales aparecen en el mismo orden en la salida ordenada que aparecen en la array de entrada que se va a ordenar.

Formalmente, la estabilidad se puede definir como,
sea una array y sea una ordenación débil estricta de los elementos de .
Un algoritmo de clasificación es estable si : ¿

dónde está la permutación de clasificación (la clasificación se mueve a la posición )
? De manera informal, la estabilidad significa que los elementos equivalentes conservan sus posiciones relativas después de la clasificación.

¿Nos interesan las arrays simples como una array de enteros?
Cuando los elementos iguales son indistinguibles, como con números enteros, o más generalmente, cualquier dato donde el elemento completo es la clave, la estabilidad no es un problema. La estabilidad tampoco es un problema si todas las teclas son diferentes.

Un ejemplo donde es útil
Considere el siguiente conjunto de datos de nombres de estudiantes y sus respectivas secciones de clase.

Si clasificamos estos datos solo por nombre, es muy poco probable que el conjunto de datos resultante se agrupe también por secciones.

Por lo tanto, es posible que tengamos que ordenar nuevamente para obtener una lista de estudiantes por sección también. Pero al hacerlo, si el algoritmo de clasificación no es estable, podríamos obtener un resultado como este:

El conjunto de datos ahora está ordenado según las secciones, pero no según los nombres.
En el conjunto de datos ordenados por nombre, la tupla estaba antes de , pero como el algoritmo de ordenación no es estable, se pierde el orden relativo.
Si, por otro lado, usáramos un algoritmo de clasificación estable, el resultado sería:

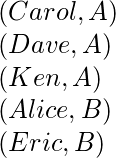
Aquí se mantiene el orden relativo entre distintas tuplas. Puede darse el caso de que el orden relativo se mantenga en un Ordenamiento Inestable pero eso es muy poco probable.

¿Qué algoritmos de clasificación son estables?
Algunos algoritmos de clasificación son estables por naturaleza, como Bubble Sort , Insertion Sort , Merge Sort , Count Sort , etc.
Las clasificaciones estables basadas en comparaciones, como Merge Sort y Insertion Sort, mantienen la estabilidad al garantizar que: El
elemento viene antes si y solo si , aquí i, j son índices y .
Dado que el orden relativo se conserva, es decir , viene antes .
Otras clasificaciones que no se basan en la comparación, como la clasificación por conteomantener la estabilidad asegurándose de que la array ordenada se llene en orden inverso para que los elementos con claves equivalentes tengan la misma posición relativa.
Algunas clasificaciones, como Radix Sort , dependen de otra clasificación, con el único requisito de que la otra clasificación sea estable.

¿Qué algoritmos de clasificación son inestables?
Quick Sort , Heap Sort , etc., se pueden hacer estables teniendo también en cuenta la posición de los elementos. Este cambio se puede hacer de una manera que no comprometa mucho el rendimiento y posiblemente ocupe algo de espacio adicional .

¿Podemos hacer que cualquier algoritmo de clasificación sea estable?
Cualquier algoritmo de clasificación dado que no sea estable puede modificarse para que sea estable. Puede haber formas específicas de clasificación de algoritmos para hacerlo estable, pero en general, cualquier algoritmo de clasificación basado en comparación que no sea estable por naturaleza puede modificarse para que sea estable cambiando la operación de comparación clave para que la comparación de dos claves considere la posición como un factor para objetos con claves iguales.

Referencias:
http://www.math.uic.edu/~leon/cs-mcs401-s08/handouts/stability.pdf
http://en.wikipedia.org/wiki/Sorting_algorithm#Stability

Este artículo es una contribución de Chirag Manwani . Si te gusta GeeksforGeeks y te gustaría contribuir, también puedes escribir un artículo usando write.geeksforgeeks.org o enviar tu artículo por correo a review-team@geeksforgeeks.org. Vea su artículo que aparece en la página principal de GeeksforGeeks y ayude a otros Geeks.

Escriba comentarios si encuentra algo incorrecto o si desea compartir más información sobre el tema tratado anteriormente.