estrategia óptima para un juego | conjunto 2

Planteamiento del problema: Considere una fila de n monedas de valores v1. . . vn, donde n es par. Jugamos un juego contra un oponente alternando turnos. En cada turno, un jugador selecciona la primera o la última moneda de la fila, la retira de la fila de forma permanente y recibe el valor de la moneda. Determine la máxima cantidad posible de dinero que definitivamente podemos ganar si nos movemos primero.
Nota: el oponente es tan inteligente como el usuario.

Entendamos el problema con algunos ejemplos:

1. 5, 3, 7, 10: el usuario recopila el valor máximo como 15 (10 + 5)
2. 8, 15, 3, 7: el usuario recopila el valor máximo como 22 (7 + 15)

¿Elegir lo mejor en cada movimiento da una solución óptima?
No. En el segundo ejemplo, así puede terminar el juego:

1. 
…….El usuario elige 8. 
…….El oponente elige 15. 
…….El usuario elige 7. 
…….El oponente elige 3. 
El valor total recopilado por el usuario es 15(8 + 7) 
2. 
…….El usuario elige 7 . 
…….El oponente elige 8. 
…….El usuario elige 15. 
…….El oponente elige 3. 
El valor total recolectado por el usuario es 22(7 + 15) 

Entonces, si el usuario sigue el segundo estado del juego, se puede recolectar el valor máximo aunque el primer movimiento no sea el mejor.
 

Hemos discutido un enfoque que hace 4 llamadas recursivas . En esta publicación, se analiza un nuevo enfoque que realiza dos llamadas recursivas.
Hay dos opciones: 

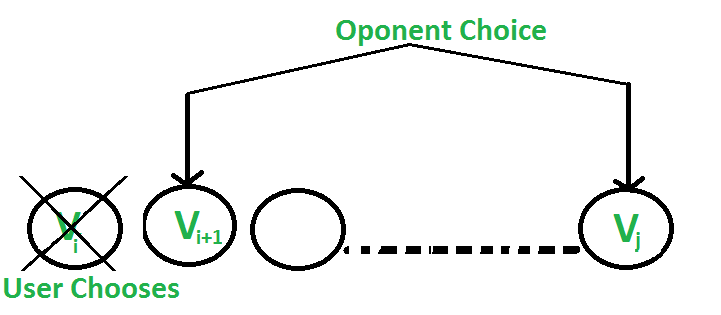
1. El usuario elige la i-ésima moneda con valor Vi: El oponente elige la (i+1)-ésima moneda o la j-ésima moneda. El oponente tiene la intención de elegir la moneda que deja al usuario con el valor mínimo. 
es decir, el usuario puede recopilar el valor Vi + (Sum – Vi) – F(i+1, j, Sum – Vi) donde Sum es la suma de las monedas del índice i al j. La expresión se puede simplificar a Sum – F(i+1, j, Sum – Vi) 
 

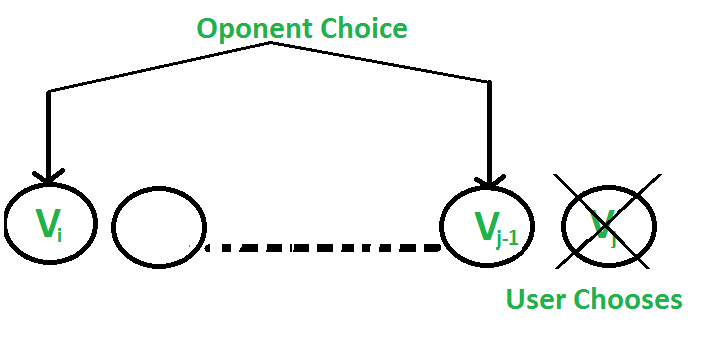
2. El usuario elige la j-ésima moneda con valor Vj: El oponente elige la i-ésima moneda o la (j-1)-ésima moneda. El oponente tiene la intención de elegir la moneda que deja al usuario con el valor mínimo. 
es decir, el usuario puede recopilar el valor Vj + (Sum – Vj) – F(i, j-1, Sum – Vj) donde Sum es la suma de las monedas del índice i al j. La expresión se puede simplificar a Sum – F(i, j-1, Sum – Vj) 
 

La siguiente es la solución recursiva que se basa en las dos opciones anteriores. Tomamos un máximo de dos opciones. 

F(i, j) representa el valor máximo que el usuario puede obtener de 

         i-ésima moneda a j-ésima moneda.

arr[] representa la lista de monedas

    F(i, j) = Max(Suma – F(i+1, j, Suma-arr[i]), 

                   Suma – F(i, j-1, Suma-arr[j])) 

Caso base

    F(i, j) = max(arr[i], arr[j]) Si j == i+1

Solución recursiva simple :

// C++ program to find out maximum value from a
// given sequence of coins
#include <bits/stdc++.h>
using namespace std;
 
int oSRec(int arr[], int i, int j, int sum)
{
    if (j == i + 1)
        return max(arr[i], arr[j]);
 
    // For both of your choices, the opponent
    // gives you total sum minus maximum of
    // his value
    return max((sum - oSRec(arr, i + 1, j, sum - arr[i])),
               (sum - oSRec(arr, i, j - 1, sum - arr[j])));
}
 
// Returns optimal value possible that a player can
// collect from an array of coins of size n. Note
// than n must be even
int optimalStrategyOfGame(int* arr, int n)
{
    int sum = 0;
    sum = accumulate(arr, arr + n, sum);
    return oSRec(arr, 0, n - 1, sum);
}
 
// Driver program to test above function
int main()
{
    int arr1[] = { 8, 15, 3, 7 };
    int n = sizeof(arr1) / sizeof(arr1[0]);
    printf("%d\n", optimalStrategyOfGame(arr1, n));
 
    int arr2[] = { 2, 2, 2, 2 };
    n = sizeof(arr2) / sizeof(arr2[0]);
    printf("%d\n", optimalStrategyOfGame(arr2, n));
 
    int arr3[] = { 20, 30, 2, 2, 2, 10 };
    n = sizeof(arr3) / sizeof(arr3[0]);
    printf("%d\n", optimalStrategyOfGame(arr3, n));
 
    return 0;
}

// Java program to find out maximum value from a
// given sequence of coins
import java.io.*;
 
class GFG {
 
    static int oSRec(int[] arr, int i, int j, int sum)
    {
        if (j == i + 1)
            return Math.max(arr[i], arr[j]);
 
        // For both of your choices, the opponent
        // gives you total sum minus maximum of
        // his value
        return Math.max(
            (sum - oSRec(arr, i + 1, j, sum - arr[i])),
            (sum - oSRec(arr, i, j - 1, sum - arr[j])));
    }
 
    // Returns optimal value possible that a player can
    // collect from an array of coins of size n. Note
    // than n must be even
    static int optimalStrategyOfGame(int[] arr, int n)
    {
        int sum = 0;
        for (int i = 0; i < n; i++) {
            sum += arr[i];
        }
 
        return oSRec(arr, 0, n - 1, sum);
    }
 
    // Driver code
    static public void main(String[] args)
    {
        int[] arr1 = { 8, 15, 3, 7 };
        int n = arr1.length;
        System.out.println(optimalStrategyOfGame(arr1, n));
 
        int[] arr2 = { 2, 2, 2, 2 };
        n = arr2.length;
        System.out.println(optimalStrategyOfGame(arr2, n));
 
        int[] arr3 = { 20, 30, 2, 2, 2, 10 };
        n = arr3.length;
        System.out.println(optimalStrategyOfGame(arr3, n));
    }
}
 
// This code is contributed by anuj_67..

# python3 program to find out maximum value from a
# given sequence of coins
 
 
def oSRec(arr, i, j, Sum):
 
    if (j == i + 1):
        return max(arr[i], arr[j])
 
    # For both of your choices, the opponent
    # gives you total Sum minus maximum of
    # his value
    return max((Sum - oSRec(arr, i + 1, j, Sum - arr[i])),
               (Sum - oSRec(arr, i, j - 1, Sum - arr[j])))
 
# Returns optimal value possible that a player can
# collect from an array of coins of size n. Note
# than n must be even
 
 
def optimalStrategyOfGame(arr, n):
 
    Sum = 0
    Sum = sum(arr)
    return oSRec(arr, 0, n - 1, Sum)
 
# Driver code
 
 
arr1 = [8, 15, 3, 7]
n = len(arr1)
print(optimalStrategyOfGame(arr1, n))
 
arr2 = [2, 2, 2, 2]
n = len(arr2)
print(optimalStrategyOfGame(arr2, n))
 
arr3 = [20, 30, 2, 2, 2, 10]
n = len(arr3)
print(optimalStrategyOfGame(arr3, n))
 
# This code is contributed by Mohit kumar 29

// C# program to find out maximum value from a
// given sequence of coins
using System;
class GFG {
    static int oSRec(int[] arr, int i, int j, int sum)
    {
        if (j == i + 1)
            return Math.Max(arr[i], arr[j]);
 
        // For both of your choices, the opponent
        // gives you total sum minus maximum of
        // his value
        return Math.Max(
            (sum - oSRec(arr, i + 1, j, sum - arr[i])),
            (sum - oSRec(arr, i, j - 1, sum - arr[j])));
    }
 
    // Returns optimal value possible that a player can
    // collect from an array of coins of size n. Note
    // than n must be even
    static int optimalStrategyOfGame(int[] arr, int n)
    {
        int sum = 0;
        for (int i = 0; i < n; i++) {
            sum += arr[i];
        }
 
        return oSRec(arr, 0, n - 1, sum);
    }
 
    // Driver code
    static public void Main()
    {
        int[] arr1 = { 8, 15, 3, 7 };
        int n = arr1.Length;
        Console.WriteLine(optimalStrategyOfGame(arr1, n));
 
        int[] arr2 = { 2, 2, 2, 2 };
        n = arr2.Length;
        Console.WriteLine(optimalStrategyOfGame(arr2, n));
 
        int[] arr3 = { 20, 30, 2, 2, 2, 10 };
        n = arr3.Length;
        Console.WriteLine(optimalStrategyOfGame(arr3, n));
    }
}
 
// This code is contributed by AnkitRai01

<script>
    // Javascript program to find out maximum value from a
    // given sequence of coins
     
    function oSRec(arr, i, j, sum)
    {
        if (j == i + 1)
            return Math.max(arr[i], arr[j]);
      
        // For both of your choices, the opponent
        // gives you total sum minus maximum of
        // his value
        return Math.max((sum - oSRec(arr, i + 1, j,
                                     sum - arr[i])),
                        (sum - oSRec(arr, i, j - 1,
                                     sum - arr[j])));
    }
      
    // Returns optimal value possible that a player can
    // collect from an array of coins of size n. Note
    // than n must be even
    function optimalStrategyOfGame(arr, n)
    {
        let sum = 0;
        for(let i = 0; i < n; i++)
        {
            sum += arr[i];
        }
  
        return oSRec(arr, 0, n - 1, sum);
    }
     
    let arr1 = [ 8, 15, 3, 7 ];
    let n = arr1.length;
    document.write(optimalStrategyOfGame(arr1, n) + "</br>");
 
    let arr2 = [ 2, 2, 2, 2 ];
    n = arr2.length;
    document.write(optimalStrategyOfGame(arr2, n) + "</br>");
 
    let arr3 = [ 20, 30, 2, 2, 2, 10 ];
    n = arr3.length;
    document.write(optimalStrategyOfGame(arr3, n) + "</br>");
 
</script>

22
4
42

Solución basada en memorización :

// C++ program to find out maximum value from a
// given sequence of coins
#include <bits/stdc++.h>
using namespace std;
 
const int MAX = 100;
 
int memo[MAX][MAX];
 
int oSRec(int arr[], int i, int j, int sum)
{
    if (j == i + 1)
        return max(arr[i], arr[j]);
 
    if (memo[i][j] != -1)
        return memo[i][j];
 
    // For both of your choices, the opponent
    // gives you total sum minus maximum of
    // his value
    memo[i][j]
        = max((sum - oSRec(arr, i + 1, j, sum - arr[i])),
              (sum - oSRec(arr, i, j - 1, sum - arr[j])));
 
    return memo[i][j];
}
 
// Returns optimal value possible that a player can
// collect from an array of coins of size n. Note
// than n must be even
int optimalStrategyOfGame(int* arr, int n)
{
    // Compute sum of elements
    int sum = 0;
    sum = accumulate(arr, arr + n, sum);
 
    // Initialize memoization table
    memset(memo, -1, sizeof(memo));
 
    return oSRec(arr, 0, n - 1, sum);
}
 
// Driver program to test above function
int main()
{
    int arr1[] = { 8, 15, 3, 7 };
    int n = sizeof(arr1) / sizeof(arr1[0]);
    printf("%d\n", optimalStrategyOfGame(arr1, n));
 
    int arr2[] = { 2, 2, 2, 2 };
    n = sizeof(arr2) / sizeof(arr2[0]);
    printf("%d\n", optimalStrategyOfGame(arr2, n));
 
    int arr3[] = { 20, 30, 2, 2, 2, 10 };
    n = sizeof(arr3) / sizeof(arr3[0]);
    printf("%d\n", optimalStrategyOfGame(arr3, n));
 
    return 0;
}

// Java program to find out maximum value from a
// given sequence of coins
import java.util.*;
class GFG {
 
    static int MAX = 100;
 
    static int[][] memo = new int[MAX][MAX];
 
    static int oSRec(int arr[], int i, int j, int sum)
    {
        if (j == i + 1)
            return Math.max(arr[i], arr[j]);
 
        if (memo[i][j] != -1)
            return memo[i][j];
 
        // For both of your choices, the opponent
        // gives you total sum minus maximum of
        // his value
        memo[i][j] = Math.max(
            (sum - oSRec(arr, i + 1, j, sum - arr[i])),
            (sum - oSRec(arr, i, j - 1, sum - arr[j])));
 
        return memo[i][j];
    }
 
    static int accumulate(int[] arr, int start, int end)
    {
        int sum = 0;
        for (int i = 0; i < arr.length; i++)
            sum += arr[i];
        return sum;
    }
 
    // Returns optimal value possible that a player can
    // collect from an array of coins of size n. Note
    // than n must be even
    static int optimalStrategyOfGame(int[] arr, int n)
    {
        // Compute sum of elements
        int sum = 0;
        sum = accumulate(arr, 0, n);
 
        // Initialize memoization table
        for (int j = 0; j < MAX; j++) {
            for (int k = 0; k < MAX; k++)
                memo[j][k] = -1;
        }
 
        return oSRec(arr, 0, n - 1, sum);
    }
 
    // Driver Code
    public static void main(String[] args)
    {
        int arr1[] = { 8, 15, 3, 7 };
        int n = arr1.length;
        System.out.printf("%d\n",
                          optimalStrategyOfGame(arr1, n));
 
        int arr2[] = { 2, 2, 2, 2 };
        n = arr2.length;
        System.out.printf("%d\n",
                          optimalStrategyOfGame(arr2, n));
 
        int arr3[] = { 20, 30, 2, 2, 2, 10 };
        n = arr3.length;
        System.out.printf("%d\n",
                          optimalStrategyOfGame(arr3, n));
    }
}
 
// This code is contributed by gauravrajput1

# Python3 program to find out maximum value
# from a given sequence of coins
MAX = 100
 
memo = [[0 for i in range(MAX)]
        for j in range(MAX)]
 
 
def oSRec(arr, i, j, Sum):
 
    if (j == i + 1):
        return max(arr[i], arr[j])
 
    if (memo[i][j] != -1):
        return memo[i][j]
 
    # For both of your choices, the opponent
    # gives you total sum minus maximum of
    # his value
    memo[i][j] = max((Sum - oSRec(arr, i + 1, j,
                                  Sum - arr[i])),
                     (Sum - oSRec(arr, i, j - 1,
                                  Sum - arr[j])))
 
    return memo[i][j]
 
# Returns optimal value possible that a
# player can collect from an array of
# coins of size n. Note than n must
# be even
 
 
def optimalStrategyOfGame(arr, n):
 
    # Compute sum of elements
    Sum = 0
    Sum = sum(arr)
 
    # Initialize memoization table
    for j in range(MAX):
        for k in range(MAX):
            memo[j][k] = -1
 
    return oSRec(arr, 0, n - 1, Sum)
 
 
# Driver Code
arr1 = [8, 15, 3, 7]
n = len(arr1)
print(optimalStrategyOfGame(arr1, n))
 
arr2 = [2, 2, 2, 2]
n = len(arr2)
print(optimalStrategyOfGame(arr2, n))
 
arr3 = [20, 30, 2, 2, 2, 10]
n = len(arr3)
print(optimalStrategyOfGame(arr3, n))
 
# This code is contributed by divyesh072019

// C# program to find out maximum value from a
// given sequence of coins
using System;
class GFG {
 
    static int MAX = 100;
 
    static int[, ] memo = new int[MAX, MAX];
 
    static int oSRec(int[] arr, int i, int j, int sum)
    {
        if (j == i + 1)
            return Math.Max(arr[i], arr[j]);
 
        if (memo[i, j] != -1)
            return memo[i, j];
 
        // For both of your choices, the opponent
        // gives you total sum minus maximum of
        // his value
        memo[i, j] = Math.Max(
            (sum - oSRec(arr, i + 1, j, sum - arr[i])),
            (sum - oSRec(arr, i, j - 1, sum - arr[j])));
 
        return memo[i, j];
    }
 
    static int accumulate(int[] arr, int start, int end)
    {
        int sum = 0;
        for (int i = 0; i < arr.Length; i++)
            sum += arr[i];
        return sum;
    }
 
    // Returns optimal value possible that a player can
    // collect from an array of coins of size n. Note
    // than n must be even
    static int optimalStrategyOfGame(int[] arr, int n)
    {
        // Compute sum of elements
        int sum = 0;
        sum = accumulate(arr, 0, n);
 
        // Initialize memoization table
        for (int j = 0; j < MAX; j++) {
            for (int k = 0; k < MAX; k++)
                memo[j, k] = -1;
        }
 
        return oSRec(arr, 0, n - 1, sum);
    }
 
    // Driver Code
    public static void Main(String[] args)
    {
        int[] arr1 = { 8, 15, 3, 7 };
        int n = arr1.Length;
        Console.Write("{0}\n",
                      optimalStrategyOfGame(arr1, n));
 
        int[] arr2 = { 2, 2, 2, 2 };
        n = arr2.Length;
        Console.Write("{0}\n",
                      optimalStrategyOfGame(arr2, n));
 
        int[] arr3 = { 20, 30, 2, 2, 2, 10 };
        n = arr3.Length;
        Console.Write("{0}\n",
                      optimalStrategyOfGame(arr3, n));
    }
}
 
// This code is contributed by Rohit_ranjan

<script>
 
// Javascript program to find out maximum
// value from a given sequence of coins
let MAX = 100;
let memo = new Array(MAX);
for(let i = 0; i < MAX; i++)
{
    memo[i] = new Array(MAX);
    for(let j = 0; j < MAX; j++)
    {
        memo[i][j] = 0;
    }
}
 
function oSRec(arr, i, j, sum)
{
    if (j == i + 1)
        return Math.max(arr[i], arr[j]);
  
    if (memo[i][j] != -1)
        return memo[i][j];
  
    // For both of your choices, the opponent
    // gives you total sum minus maximum of
    // his value
    memo[i][j] = Math.max((sum - oSRec(arr, i + 1, j,
                                       sum - arr[i])),
                          (sum - oSRec(arr, i, j - 1,
                                       sum - arr[j])));
  
    return memo[i][j];
}
 
function accumulate(arr, start, end)
{
     let sum = 0;
    for(let i = 0; i < arr.length; i++)
        sum += arr[i];
         
    return sum;
}
 
// Returns optimal value possible that a player can
// collect from an array of coins of size n. Note
// than n must be even
function optimalStrategyOfGame(arr, n)
{
     
    // Compute sum of elements
    let sum = 0;
    sum = accumulate(arr, 0, n);
  
    // Initialize memoization table
    for(let j = 0; j < MAX; j++)
    {
        for(let k = 0; k < MAX; k++)
            memo[j][k] = -1;
    }
    return oSRec(arr, 0, n - 1, sum);
}
 
// Driver Code
let arr1 = [ 8, 15, 3, 7 ];
let n = arr1.length;
document.write(
    optimalStrategyOfGame(arr1, n) + "<br>");
                
let arr2 = [ 2, 2, 2, 2 ];
n = arr2.length;
document.write(
    optimalStrategyOfGame(arr2, n) + "<br>");
                
let arr3 = [ 20, 30, 2, 2, 2, 10 ];
n = arr3.length;
document.write(
    optimalStrategyOfGame(arr3, n) + "<br>");
 
// This code is contributed by patel2127
 
</script>

22
4
42

Otro enfoque: otra idea para resolver fácilmente el problema es:

Si denotamos las monedas recolectadas por nosotros como una puntuación positiva de una cantidad equivalente, mientras que las monedas retiradas por nuestro oponente con una puntuación negativa de una cantidad equivalente, entonces el problema se transforma en maximizar nuestra puntuación si vamos primero. 

Denotemos dp[i][j] como la puntuación máxima que un jugador puede obtener en el subarreglo [i . . . j] , luego
dp[i][j] = max(arr[i]-dp[i+1][j], arr[j]-dp[i][j-1])

Esta relación de programación dinámica se puede justificar como se menciona a continuación:

Esta relación se cumple porque 

• Si elegimos el elemento más a la izquierda, obtendríamos una puntuación equivalente a 
  arr[i]: la cantidad máxima que nuestro oponente puede obtener del subarreglo [(i+1) … j] . 
• Del mismo modo, elegir el elemento más a la derecha nos dará una puntuación equivalente a 
  arr[j]: la cantidad máxima de puntuación que nuestro oponente obtiene del subarreglo [i … (j-1)] . 

Esto se puede resolver utilizando la relación de programación dinámica simple dada anteriormente. La respuesta final estaría contenida en dp[0][n-1] .

Sin embargo, todavía tenemos que tener en cuenta el impacto de la introducción de la puntuación negativa. 

Supongamos que dp[0][n-1] es igual a VAL , la suma de todas las puntuaciones es igual a SUM y la puntuación total de nuestro oponente es igual a OPP , 

• Luego, de acuerdo con el problema original, se supone que debemos calcular abs(OPP) + VAL, ya que nuestro oponente no tiene ningún impacto negativo en nuestra respuesta final de acuerdo con el enunciado del problema original. 
• Este valor se puede calcular fácilmente como,
  VAL + 2*abs(OPP) = SUMA     
  (OPP eliminado por nuestro oponente implica que también habíamos ganado la cantidad de OPP, por lo tanto, 2*abs(OPP))
  => VAL + abs(OPP) ) = (SUMA + VALOR)/2

La implementación del enfoque anterior se da a continuación.

#include <bits/stdc++.h>
using namespace std;
 
// Function to find the maximum possible
// amount of money we can win.
long long maximumAmount(int arr[], int n)
{
    long long sum = 0;
    vector<vector<long long> > dp(n,
                                  vector<long long>(n, 0));
    for (int i = (n - 1); i >= 0; i--) {
         
        // Calculating the sum of all the elements
        sum += arr[i];
        for (int j = i; j < n; j++) {
            if (i == j) {
                 
                // If there is only one element then we
                // can only get arr[i] score
                dp[i][j] = arr[i];
            }
            else {
                // Calculating the dp states
                // using the relation
                dp[i][j] = max(arr[i] - dp[i + 1][j],
                               arr[j] - dp[i][j - 1]);
            }
        }
    }
    // Equating and returning the final answer
    // as per the relation
    return (sum + dp[0][n - 1]) / 2;
}
 
// Driver Code
int main()
{
    int arr1[] = { 8, 15, 3, 7 };
    int n = sizeof(arr1) / sizeof(arr1[0]);
    printf("%lld\n", maximumAmount(arr1, n));
 
    return 0;
}
// This code is contributed by Ojassvi Kumar

22

Este enfoque es sugerido por Ojassvi Kumar .